This post is a part of Rethink Priorities’ Worldview Investigations Team’s CURVE Sequence: “Causes and Uncertainty: Rethinking Value in Expectation.” The aim of this sequence is twofold: first, to consider alternatives to expected value maximization for cause prioritization; second, to evaluate the claim that a commitment to expected value maximization robustly supports the conclusion that we ought to prioritize existential risk mitigation over all else. This post examines how uncertainty increases over time and estimates a model of how a Bayesian would interpret increasingly uncertain forecasts.
Executive summary
- We face a trade-off when deciding between actions with short- versus long-run impacts: on the one hand, predictions of short-run impacts are more certain, but their expected value may be lower; on the other, the expected value of long-run impacts may be larger, but the predictions on which they’re based are more uncertain. If uncertainty rises faster than impact, then we may prefer the action with smaller but more certain impacts. What can we say, if anything, about the rate at which uncertainty increases as the time horizon of the prediction increases?
- In this post, I offer some empirical estimates of how quickly uncertainty about impact rises over the range of 1-20 years using data from various development economics randomized controlled trials. I make statistical predictions of the impacts over various time horizons and compare these to the true results.
- I then use and extrapolate from these results to estimate a model of Bayesian updating that formally combines the signal from such predictions with a prior to produce a posterior distribution of the impact, under some strong simplifying assumptions. When the signal has low uncertainty, the posterior is primarily determined by the signal. I show how as the noise of the signal increases over time, the posterior is increasingly determined by our prior expectations.
- Even with a gradual increase in uncertainty over time, the posterior expected value of long-run impacts shrinks towards 0 as time progresses. My preferred, best-case estimates say that the posterior expected value is 10% of the signal expected value after 561 years and 1% after 6,168 years, although I show that these estimates themselves are highly uncertain and sensitive to modeling choices.
- I discuss the limitations of this work and the upshots for interpreting quantitative models that include very long-run effects, such as Rethink Priorities’ forthcoming Cross-Cause Cost-Effectiveness Model (CCM). As the estimates of the impact of x-risk and other far-future-focused interventions are less certain, these estimates should play a relatively smaller role in your all-things-considered view than the more certain short-run effects.
Introduction
When we evaluate interventions, a challenge arises when comparing short-term to long-term impacts: short-term predictions are generally more precise but may have smaller impacts, while long-term predictions might be suggestive of larger impacts but come with increased uncertainty. This prompts the question: as prediction horizons lengthen, how does uncertainty around these predictions increase? And what does this uncertainty imply for our all-things-considered beliefs about the relative impact of short and long-run interventions?
To address this, I employ data from various development economics randomized controlled trials (RCTs), making statistical predictions of impacts over time spans ranging from 1 to 20 years. I use the surrogate index method to make predictions and the dataset of the predictions comes from an associated paper (EA Forum post) co-authored with Jojo Lee and Victor Wang. I compare these predictions to the observed impacts from the RCTs outcomes to measure forecast error.
I correct the predictions to remove bias and then use the corrected estimates of forecast error to assess how uncertainty increases over time using graphs and meta-analysis. I show that over the 20 years in my data, forecast noise increases fairly gradually. Furthermore, the relationship between noise and time horizon is roughly linear, although the power of the data to detect non-linearities is limited.
To assess how this increase in forecast noise might affect our relative valuation of interventions with short and long-run impacts, I then use these empirical estimates to estimate a Bayesian updating model introduced by Duncan Webb.
To build intuition for how the model works, imagine we produce an estimate of the expected value of some intervention using a quantitative method, like the surrogate index or an informal back of the envelope calculation (BOTEC). Call this estimate a signal. In this classic post, Holden Karnofsky argues that we should not take signals of this type literally. Instead, we should combine the signal with a prior distribution, our beliefs before we saw the signal. Once we combine our prior with the signal, we get a posterior distribution of the impact of an action. Importantly, our posterior distribution depends on how noisy the signal is. The noisier the signal, the closer the expected value of our posterior distribution remains to our prior. For example, we would probably think a BOTEC done in 2 minutes produces a much noisier signal than a well-executed RCT and so, if both produced the same signal, but with different levels of precision, the RCT would shift the expected value of our posterior further away from the prior.
Now imagine our quantitative method produces two signals; one for the short-run value of the intervention (say, the effect after 1 year) and one for the long-run (say, the effect after 50 years). It seems reasonable to assume that the 1-year signal will be more precise than the 50-year signal. If we modeled the impact of a cash transfer from GiveDirectly, we’d be fairly confident in the precision of the signal for the effect on outcomes like consumption and savings after 1 year. However, the signal for the effect after 50 years would be much less precise: we’d have to assess whether the cash transfer is likely to kickstart a persistent growth in income, look at multigenerational effects, consider how the economy as a whole would be affected, and so on. In other words, the variance or the noise of this 50-year signal would be much greater than the variance of the 1-year signal. As such, we would put less weight on the 50-year signal than the 1-year signal when forming our posteriors for the short- and long-run values of the intervention.
Webb formalizes and extends this idea in an economic model of Bayesian updating. In Webb’s model we receive unbiased signals of the expected value of an intervention at each time period t in the future (e.g., the signals come from a BOTEC or some other quantitative method). Importantly, the noise on these signals increases as the time horizon increases and we look further into the future. This captures the intuition from above, that uncertainty increases with time horizon. What matters in the model is the rate at which the noise on the signals increases. If the noise increases sufficiently fast, then the posterior expected value of the long-term effects of an intervention may be smaller than the posterior expected value of the short-run effects of that intervention, even if the long-term expected value signals are far greater than the short-run signals.
I use data on statistical forecasts of the long-run results of RCTs to empirically estimate this model of Bayesian updating (explained in more detail below). As mentioned above, I find a gradual increase in signal/forecast noise. Despite this gradual increase, if we extrapolate forward linearly, the posterior expected value of the long-run effects of an intervention shrinks significantly towards the expected value of the prior, which I assume to be 0. With my preferred, best-case estimates, the posterior expected value is 10% of the signal expected value after 1,600 years. After 18,000 years, the posterior expected value is 1% of the signal expected value. In other words, if we received a signal that an intervention produced 100 utils each year, then our posterior expected value would be 10 utils after 1,600 years, and only 1 util after 18,000 years.
I explore a number of different cases as robustness checks and show how allowing for non-linearities in the relationship between forecast error and horizon can result in a very wide range of results. I note that all the results are dependent on the strong theoretical and empirical assumptions I make regarding the structure of the prior and the signal, and extrapolation across time. Relaxing these assumptions may significantly change the relationship between the signal and the posterior expected value. Similarly, using different data sources may also change these relationships significantly in either direction. I discuss these limitations further at the end.
This report has implications for how we interpret the results of quantitative models such as Rethink Priorities’ forthcoming Cross-Cause Cost-Effectiveness Model (CCM). We should think like Bayesians when we interpret the results or signals of such models. When the signals are about short-term value and we think the signals are relatively precise, they should play a relatively large role in forming our posterior distribution or our all-things-considered view. On the other hand, some of the signals about long-term value depend on projections up to several billion years into the future. They are much less precise as they depend on many parameters about which we might be deeply uncertain. As a result, when we integrate these signals into our all-things-considered view, we should place less weight on them relative to the more precise short-run effects. Within the CCM, we can quantify the uncertainty of estimates due to parameter uncertainty, but, as with most models, we’re unable to quantify model uncertainty—the concern that we are using the wrong model—and this model uncertainty might be the dominant source of our uncertainty, especially for more speculative long-run value estimates.
In the rest of the report, I go into the theory behind Bayesian updating with increasing uncertainty over time. I then describe the data I use, how to estimate forecast noise and how to estimate the relationship between time horizon and forecast noise while dealing with potential confounding. I show how forecast noise changes over time horizon in my dataset and use this to estimate how much the signal expected value should be adjusted to end up with a Bayesian posterior expected value. I explore a number of different cases and conclude by discussing the limitations of this approach and potential improvements in future work.
Theory
In this section I first explain the key parts of a model of Bayesian updating with noisy signals from Webb (2021) that justifies putting less weight on noisier expected value signals.
Model
An agent uses a quantitative method to predict the benefit of an intervention for each future time period. These predictions are referred to as signals.
Let represent the signal for the benefit at time . This signal is composed of two parts:
- The true benefit
- A noise component
Mathematically, we can express this as:
We make two key assumptions about the noise component :
- Unbiasedness: The noise is unbiased, meaning its expected value is zero. This implies that, on average, the signal neither overestimates nor underestimates the true benefit.
- Normality: The noise follows a normal distribution centered around 0.[1]
To capture the intuition that the model is less predictive when the time horizon increases, we assume that the noise on the signal increases with the time horizon, that is:
, where with
We next make the assumption that the agent’s prior belief over the benefit is also normally distributed with mean zero and constant variance. A mean zero prior implies that before doing any research about the intervention, the agent believes that the intervention is most likely to have no impact and that positive and negative effects are equally likely (in each time period).
We discuss how reasonable these assumptions about the prior and the signal are in the Limitations - Model assumptions section below.
With these assumptions in place, we can derive the agent's posterior expected value of the intervention at each time period (see Proposition 1 in Gabaix and Laibson (2022) and proof of Proposition 1 in Appendix A).
captures how much weight the agent puts on the signal. Alternatively, it captures how much the agent ‘discounts’ the signal solely due to the uncertainty surrounding the signal. In the specific case where the prior is mean 0 and the signal is mean 1, represents the posterior expected value.
The signal reflects both the true value of the intervention and noise . When the noise in the signal is low relative to the noise in the prior, then the signal is informative about the true value of and is small so is close to 1. As such, the agent’s posterior expected value will be close to the signal . On the other hand, when the signal is noisier it is less informative and the agent’s posterior will not be shifted as much by the signal and instead will remain closer to the prior (of 0 in this model). As the noise of the signal grows over time (as ), this means that the weight, , that the agent gives to the signal will shrink over time and the posterior expected value will depend less on the signal and more on the prior.
Data
I use the data from Bernard et al. (2023) which tests a statistical method, the surrogate index, for forecasting the 1 to 20 year results of RCTs in development economics. This method does not produce Tetlockian subjective judgemental forecasts that readers may be more familiar with. Instead it produces statistical forecasts; the output from a purely statistical model which doesn’t depend on priors. This means the forecasts from the surrogate index method dovetail nicely with the definition of signals in the Bayesian updating model described above. We know the actual results of the RCTs so we can evaluate the forecasts, which means we can empirically estimate the rate at which signal noise increases and therefore estimate the Bayesian updating model.
The surrogate index method was developed by Athey et al. (2019) to predict long-term treatment effects. The method combines two datasets (1) a short-term RCT where we observe short-term outcomes but don’t observe the long-term outcomes, and (2) an observational dataset where we observe the long-term outcomes as well as the same set of short-term outcomes, but for a different sample of individuals. Here’s a simplified breakdown of how the method works:[2]
- We use the observational dataset to train a predictive model. This model predicts the long-term outcomes from the short-term outcomes.
- We use the predictive model, trained in the previous step, to predict the long-term outcomes in the short-term RCT.
- We take the difference between the forecasted long-term outcomes in the treatment and control groups in the RCT, to estimate the long-term treatment effect.
In Bernard et al. (2023), we conducted an empirical analysis of the performance of the surrogate index method using real-world long-run RCTs spanning 5 to 20 years. Here's our approach:
- Estimation of true long-run effect: We started by estimating the true long-run treatment effect using long-run data directly from these RCTs.
- Implementation of surrogate index: Next, instead of using the long-run data, we applied the surrogate index method to predict the long-run treatment effect indirectly. We did this using various short-run outcomes observed at different times. This leads to multiple predictions of each long-run treatment effect, each with different time horizons.[3]
- Calculation of Forecast Error: We then compared the direct long-run treatment effect estimate from the RCTs to our predictions from the surrogate index method. The differences between these estimates gave us the forecast error for the surrogate index approach.
In this post, I use the data from 8 different RCTs to estimate the relationship between time horizon and forecast noise. A summary of the RCTs is presented in table 1. These RCTs are broadly representative of the medium to long-run development economics literature with a number of common development interventions and studies from Latin America, South Asia and East Africa.
Table 1. Summary of RCTs used in analysis
| Paper | Intervention | Country | Years | Waves | Arms |
| Barrera et al. 2019 | Conditional cash transfer | Colombia | 12 | 5 | 5 |
| Duflo et al. 2015 | Grant & HIV course | Kenya | 7 | 3 | 4 |
| De Mel et al. 2012 | Cash grant | Sri Lanka | 5 | 12 | 3 |
| Blattman et al. 2020 | Cash Grant | Uganda | 9 | 3 | 2 |
| Banerjee et al. 2021 | Graduation program | India | 7 | 3 | 2 |
| Baranov et al. 2020 | Psychotherapy | Pakistan | 7 | 3 | 2 |
| Gertler et al. 2012 | Conditional cash transfer | Mexico | 6 | 7 | 2 |
| Hamory et al. 2021 | Deworming | Kenya | 20 | 4 | 2 |
Notes: Waves is the number of post-treatment survey waves, it does not include pre-treatment survey waves. Arms is the number of treatment arms and includes both treatment and control group arms.
We look at the treatment effects for as many of the treatments and outcomes included in the relevant paper for each RCT. Although these outcomes may be in different units (e.g. income in dollars and weight in kilograms) we make the treatment effects comparable by (1) converting them into effect size units by dividing by the control group standard deviation and (2) flipping the signs so a positive treatment effect is always socially beneficial.
Methodology
In this section I explain how we can measure noise from our surrogate index forecast data (recall that the surrogate index forecasts are equivalent to signals in the theoretical model described above). I then explain how I use the forecast data to measure the relationship between forecast precision and time horizon. In particular, I show how to better deal with potential confounding of the relationship between time horizon and forecast precision.
Measuring forecast noise
We need to measure how the noise of forecasts changes with forecast time horizon (i.e. the function ). However, forecast noise is typically not directly measured . Instead, what is measured is an accuracy metric such as the Mean Squared Error (MSE), which is a generalized version of the Brier Score which may be more familiar to some readers.[4] For MSE, the outcome to be forecast is typically the value of some future variable which is not necessarily bounded above or below. An example here is a prediction of the inflation rate in 2024, which could be either positive or negative.
where is a forecast of outcome . This essentially takes the difference between the forecast and the outcome (e.g. the difference between forecasted inflation and actual inflation), squares it (which always results in a positive number), and then takes the mean of this across many such forecasts and outcomes.
I now show how we can go from the MSE to a measure of forecast noise. An important feature of the MSE is that it can be decomposed into Bias and Variance (or in other words, bias and noise).
If we can assume that forecasts are unbiased so , then and we have a measure of forecast noise. What does it mean intuitively for forecasts to be unbiased?
In the context of MSE, forecasts being unbiased means that forecasts neither systematically overestimate nor underestimate the true outcomes so there’s no consistent error in one direction. In the inflation context, this means that if half of the forecasts are overestimates of the inflation rate, the other half need to be equally-sized underestimates, to produce a set of unbiased forecasts.[5] In our theoretical model, this would mean that the signals are on average neither overestimating or underestimating the benefit of the intervention.
Unbiasedness:
For MSE, if the average error of forecasts (on outcomes with a common unit) is 0 then the bias component is 0 and we can use MSE as a measure of forecast noise. If we know a set of forecasts has a systematic bias, meaning they consistently overestimate or underestimate the true outcomes, we can correct for this bias by adjusting each forecasted value accordingly. To produce unbiased forecasts, we simply need to subtract the known bias from each forecasted value. By doing this, the average error between the forecasts and the true outcomes is reduced to zero, effectively removing the bias. See a proof of this in the appendix.
We can then compute the MSE of the corrected forecasts which will then correspond to the variance, since the bias of these forecasts is zero. For instance, if forecasts of inflation are on average 1 percentage point higher than the true level of inflation, then we can debias the forecasts of inflation by subtracting 1 percentage point from all of them, and compute the MSE of these corrected forecasts. Then the MSE of these bias-corrected forecasts is a measure of forecast noise or variance.
Estimating forecast horizon and noise relationship
Previous studies have looked at the relationship between forecast accuracy and forecast horizon (Dillon, 2021; Niplav, 2022; Prieto, 2022). An often-noted difficulty in this analysis is forecast difficulty being a confounding variable. If the selected long-range questions are ‘easier’ then if we observe no relationship between accuracy and horizon, this could be explained by the difference in easiness across different horizons, rather than there being no relationship between horizon and accuracy.[6] As Prieto (2022) writes:
One possible explanation is question selection. Grant investigators may be less willing to produce long-range forecasts about things that are particularly hard to predict because the inherent uncertainty looks insurmountable. This may not be the case for short-range forecasts, since for these most of the information is already available. In other words, we might be choosing which specific things to forecast based on how difficult we think they are to forecast regardless of their time horizon, which could explain why our accuracy doesn’t vary much by time horizon.
One way to deal with this issue is to control for the difficulty of questions. However, sadly it’s not the case that forecast questions come naturally to us with some metric of how difficult they are. As Dillon (2021) says:
Attempting to control for the difficulty of questions seems particularly useful. In practice, the difficulty of a question is not easily established before the fact, but making sets of questions that are on common topics or otherwise similar might be a good starting point here.
Given that we don’t observe forecast difficulty and therefore can’t explicitly control for it, what can we do? Instead of comparing forecasts with different ranges across different questions with different ranges, we can instead look at accuracy within questions, as Niplav (2022) does in their final section. More formally, we can do this by including ‘question fixed effects’ when we analyze the relationship between accuracy and horizon. This ensures that we compare within each question how much accuracy changes when the horizon is short versus long.
As an example, in our surrogacy data this would be: how much less accurate are we when we use 2 years of data to predict the 10 year effect of deworming on income (an 8 year forecast horizon), versus when we use 6 years of data to predict the 10 year effect (a 4 year forecast horizon). By including a question fixed effect, we ensure that features that vary across questions such as question difficulty, are controlled for and do not confound the estimated relationship between forecast horizon and accuracy.
This however requires more from our data. We now need to have multiple forecasts made at different times for each question. If we only had one forecast per question, then there would not be any within-question variation of forecast horizon, which is necessary to identify the relationship between horizon and accuracy when using fixed effects. The data we use has this feature, but other datasets with which you might want to run this analysis do not (discussed in more detail in Limitations - Data below). If you were to do this sort of analysis with such other datasets, you would likely better identify the unconfounded relationship between forecast horizon and accuracy by including forecaster and/or topic fixed effects (to ensure your comparisons are within forecaster and topic respectively).
Results
Debiased errors
First we have to remove the bias from the forecasts so that the corrected forecasts are unbiased and therefore the MSE of the corrected forecasts is equivalent to the variance or forecast noise. To do this, we estimate the mean forecast error, the average difference between the forecasted treatment effect and the actual treatment effect. As the two treatment effects are themselves estimates with noise, the error of each forecast also has some noise. We therefore use a meta-analysis to estimate the mean error by giving more weight to more precisely estimated errors and to account for the correlation between error estimates within the same study.[7] This gives us a mean error of -0.047 as shown in Table 2. In other words, on average the surrogate index approach underestimates the benefits of treatment by 0.047 standard deviations.
Table 2: Average error from meta-analysis
| Mean | Standard error | Standard deviation | |
|---|---|---|---|
| Error | -0.047 | 0.027 | 0.133 |
We therefore correct the surrogate index forecasts by adding 0.047 to all of them and this ensures that the bias of the full set of bias-corrected forecasts is now 0.[8] We then recalculate the error for each of the corrected forecasts and square these corrected errors to get our squared errors. With these squared errors in hand, we can now compute the mean squared error which is now equivalent to forecast noise.
Errors over time
Next, we plot the relationship between mean squared error and forecast horizon in figure 1. We do this separately for each study in the top half of the figure and for all studies combined in the bottom half of the figure. The lines of best fit for each plot capture the mean squared error, as flexibly estimated using LOESS smoothing.
Figure 1: Squared errors over time horizon with non-parametric lines of best fit
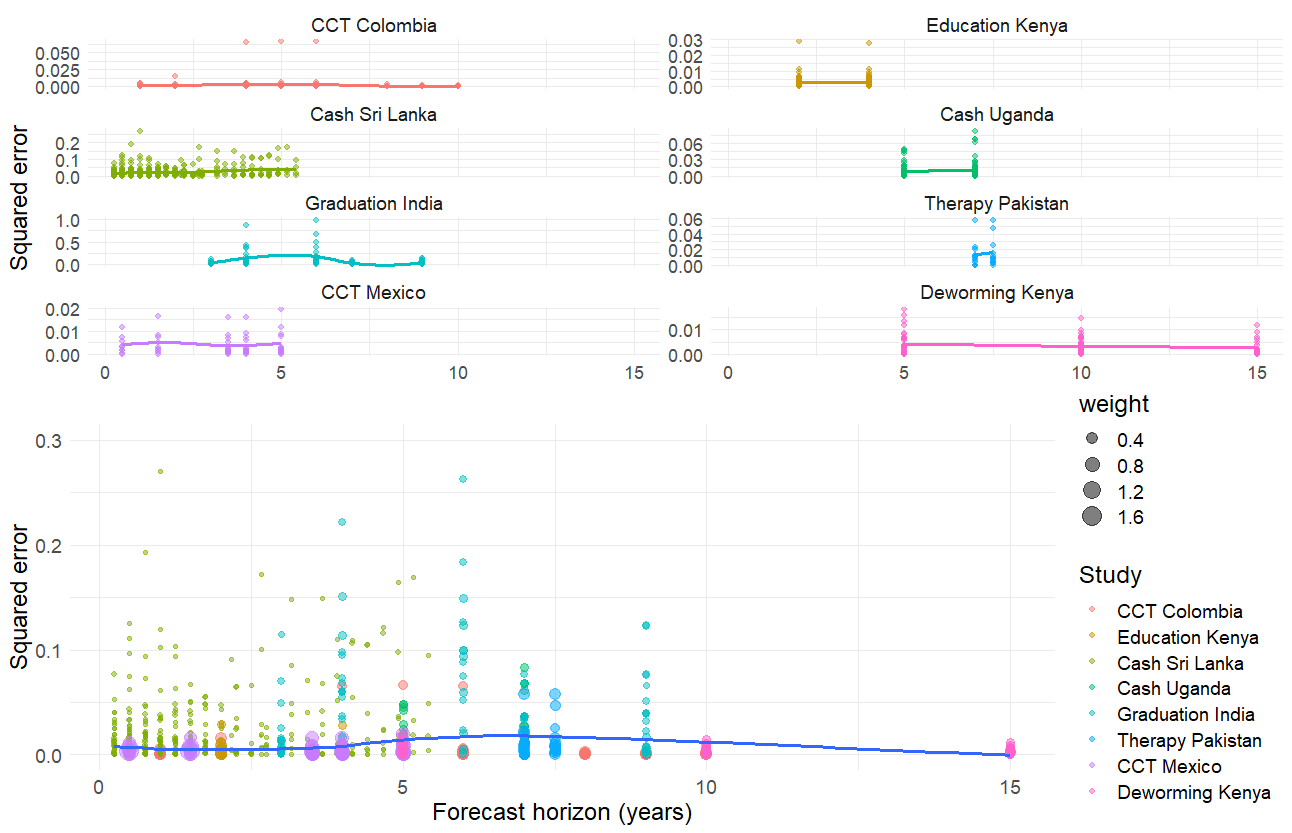
Figure 1 shows us that across all studies there is not a strong relationship between forecast horizon and forecast noise, although there is some variation within each study. The relationship is roughly linear in all studies, although the power to detect nonlinearities in this data is limited. However, in this analysis, the relationship between forecast horizon and forecast noise is possibly confounded by differences in forecast question difficulty, e.g., forecasting the impact of deworming on income may be more difficult than forecasting the impact of deworming on height. As such, we need to run a meta-regression where we include fixed effects to control for question difficulty.
Table 3: Horizon meta-regression results
| Coefficient | Estimate | Standard error | 95% confidence interval |
|---|---|---|---|
| Horizon (years), question fixed effects | 0.0009 | 0.0011 | [-0.0013, 0.0031] |
| Horizon (years), no fixed effects | 0.0026 | 0.0016 | [-0.0006, 0.0058] |
Notes: Forecast question fixed effects are included in the meta-regression in the first row but not shown in this table. The meta-regression is estimated without an intercept in both cases under the assumption that error should be 0 for forecasts with horizon zero.
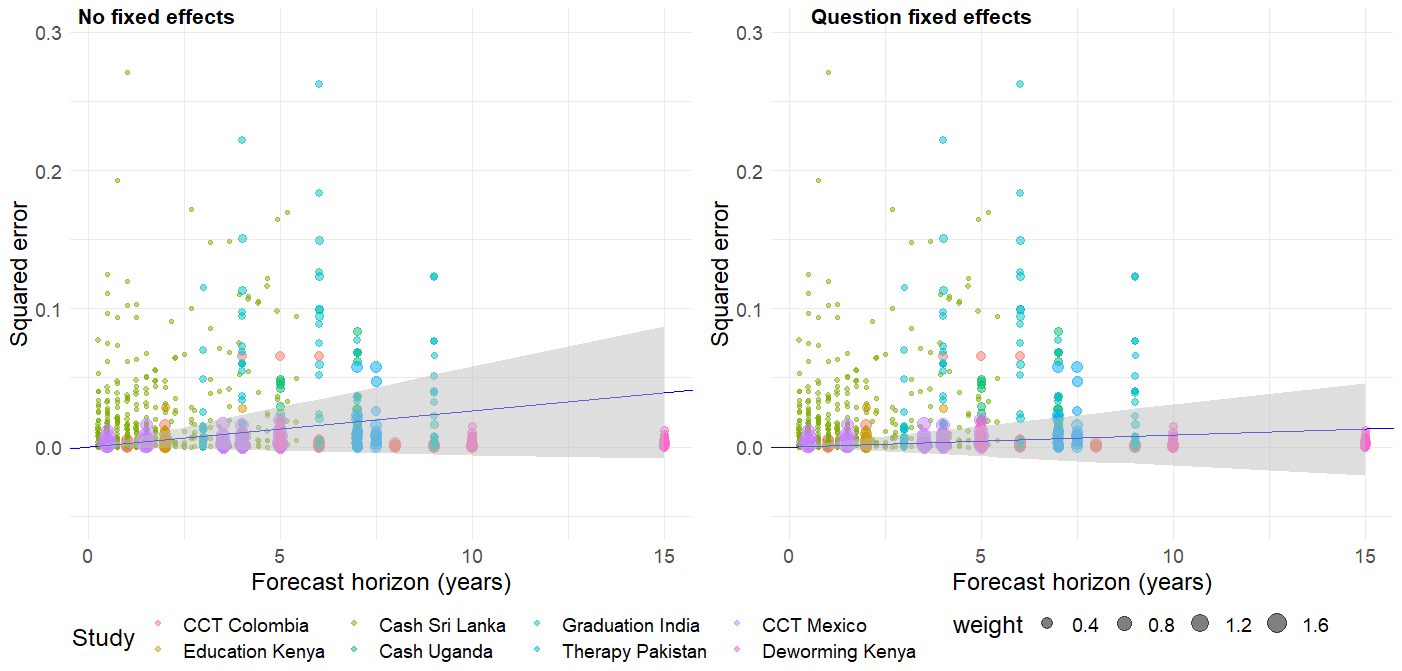
Table 3 shows us the results of the meta-regression with and without these question-fixed effects. With fixed effects, which is my preferred specification, the coefficient on horizon is slightly positive at 0.0009 but statistically insignificant with a standard error of 0.0011. Taken literally, the coefficient means that the squared error increases by 0.0009 every year, or 0.09 every 100 years. This is a very small annual increase. A common, although often critiqued, rule of thumb in psychology is that a 0.2 effect size is small. With the estimated rate of increase, it would take 231 years for the MSE to reach 0.2.[9] However, the 95% confidence interval on this estimate includes 0 and a coefficient of 0 taken literally would imply that forecast noise does not change with time horizon.
If we do not include fixed effects, the coefficient is three times larger, 0.0026, but this is still a small annual increase. Due to a slightly larger standard error, the 95% confidence interval on this estimate also includes zero. We plot the results of the meta-regressions with the 95% confidence intervals in Figure 2 below.
Figure 2: Squared errors over time horizon with fixed effect meta-regression line of best fit
Bayesian updating
Linear increase
With these measures of the relationship between forecast/signal noise and time horizon, we can now estimate , which determines how much weight an agent in our model would put on the long-run signals. In this section, I make the heroic assumption that the linear rate of increase of signal noise estimated in the previous section continues indefinitely. In the following section, I relax this assumption and allow for non-linear increases, but still extrapolate forward into the far future. I estimate the Bayesian updating model described above, seeing what the increasing signal noise implies for the posterior expected value after seeing long-run signals.
I use the variance of the average treatment effect from the true long-term RCTs (0.054) as the variance of the prior in the model[10] and keep the mean of the prior as 0. I assume the mean of the signal is 1 each period to ease interpretation, and I use the coefficient from the meta-regressions in Table 3 as the rate at which the signal noise increases each year (0.0009 and 0.0026). As robustness checks, I also use the upper ends of the 95% confidence intervals as worst-case estimates (, and ).[11]
Figure 3: Posterior expected value from forecast signal with expected value 1 and linearly increasing noise over time, 1,000 years, level-level scale
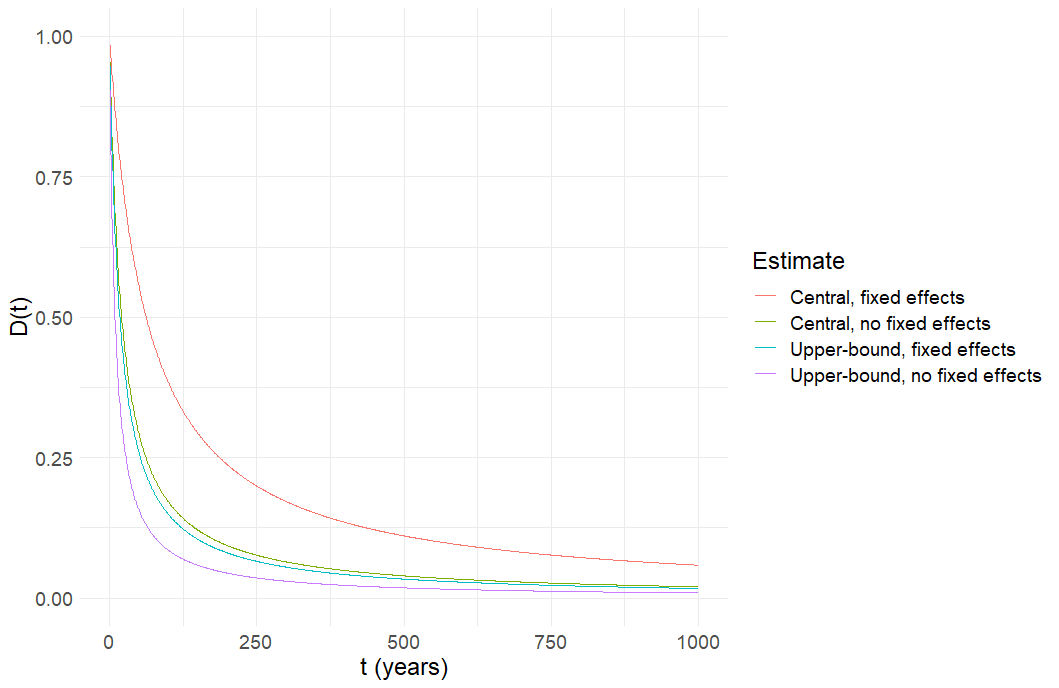
Figure 3 shows how the expected value of the posterior drops off over 1,000 years assuming a constant mean 0 and variance prior, and a constant mean 1 but increasingly noisy signal. The 4 different lines correspond to the different (linear) rates of signal noise increase described above. The downward slope of the curves shows how the agent puts less weight on the signals as time progresses, due to the increasing noise of the signals. The curves are convex which implies that there is a decreasing rate of decrease of the expected value of the posterior over time. This is because the function is defined with the signal noise in the denominator, which generates a non-linear relationship between and , even when signal noise increases linearly with t.
As the graph quickly asymptotes towards 0 and the lines become indistinguishable in a level-level graph past 1,000 years, in Figure 4 we plot a log-log graph to better see the differences when the posterior expected values and time horizons span several orders of magnitude.
Figure 4: Posterior expected value from forecast signal with expected value 1 and linearly increasing noise over time, 1,000,000 years, log-log scale
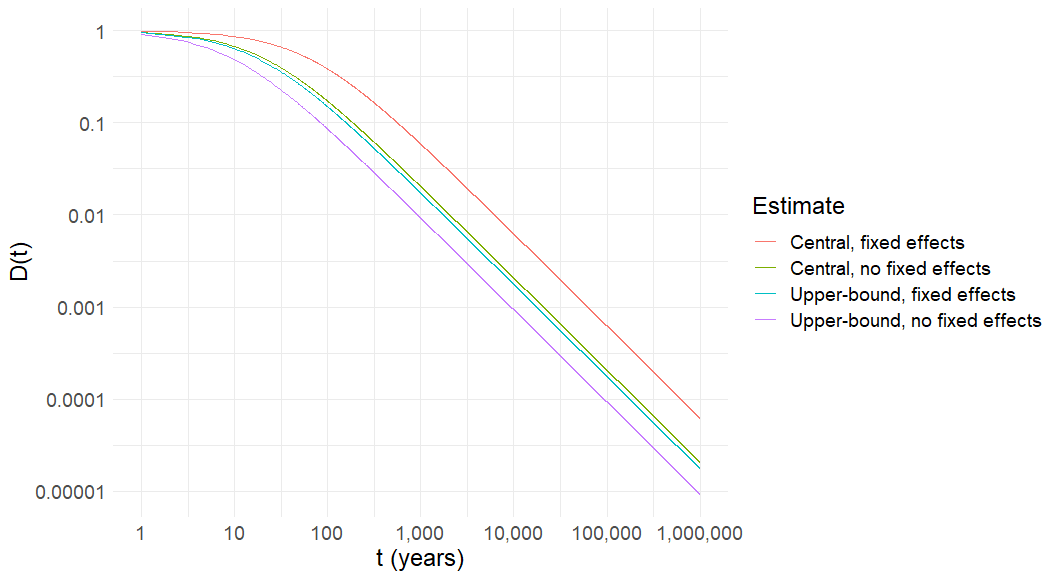
In Figure 4, we can see that the central estimate with question fixed effects (the preferred estimate) is the one that places the most weight on the signal at any point in time. This is because it is the estimate with the smallest rate of increase of forecast noise. The central fixed effects estimate has a posterior expected value approximately an order of magnitude greater than the estimate with the greatest rate of signal noise increase, the upper bound of the no-fixed-effects estimate.
When both axes are on a logarithmic scale, the rate of change appears linear if the underlying relationship between and is exponential. In the left side part of the graph, when and therefore signal noise is small, the constant prior variance is somewhat influential in determining the posterior expected value. On the right side part of the graph, the prior variance becomes negligible as the signal noise continually increases and it is the signal noise that mostly determines the relationship between and .
Non-linear increase
The previous section made the strong assumption that the rate of signal noise increase is constant over time. This is compatible with the data observed in Figure 1, but it is clearly a reach to assume that the pattern observed over 20 years of forecast data will continue indefinitely into the future. What happens if we allow for non-linearities in the rate of increase? To do this, we can model forecasting error over time as follows:
where
In the previous section, (or one of our other estimated values of forecast noise increase), and we implicitly assumed that . Now, we model the relationship with , i.e., 2/3 and 3/2. If , this implies that the rate of increase of signal noise increases over time. Conversely, if , then the rate of increase decreases over time. The relationship between forecast/signal noise and time under these assumptions is shown in Figure 5.
Figure 5: Forecast noise over time under different non-linear assumptions
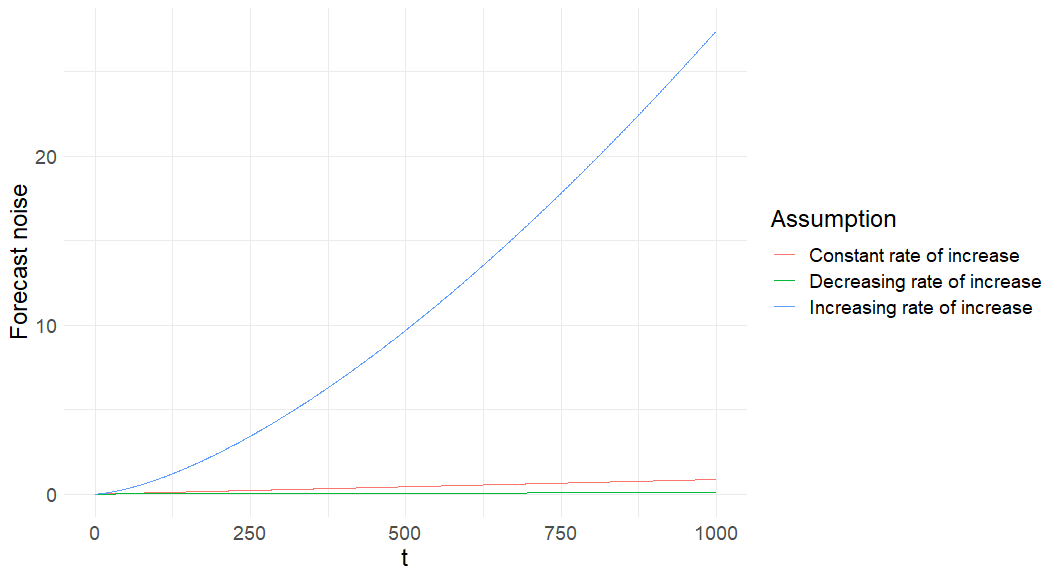
Ideally, we would estimate the parameter empirically, but estimating non-linear relationships requires a lot more data. As such, this analysis should be seen as a robustness check more than a main result, and it is again subject to the caveat that we are making extreme extrapolations into the future from limited data.
Figure 6: Posterior expected value from forecast signal with expected value 1 and non-linearly increasing noise over time, 1,000,000 years, log-log scale
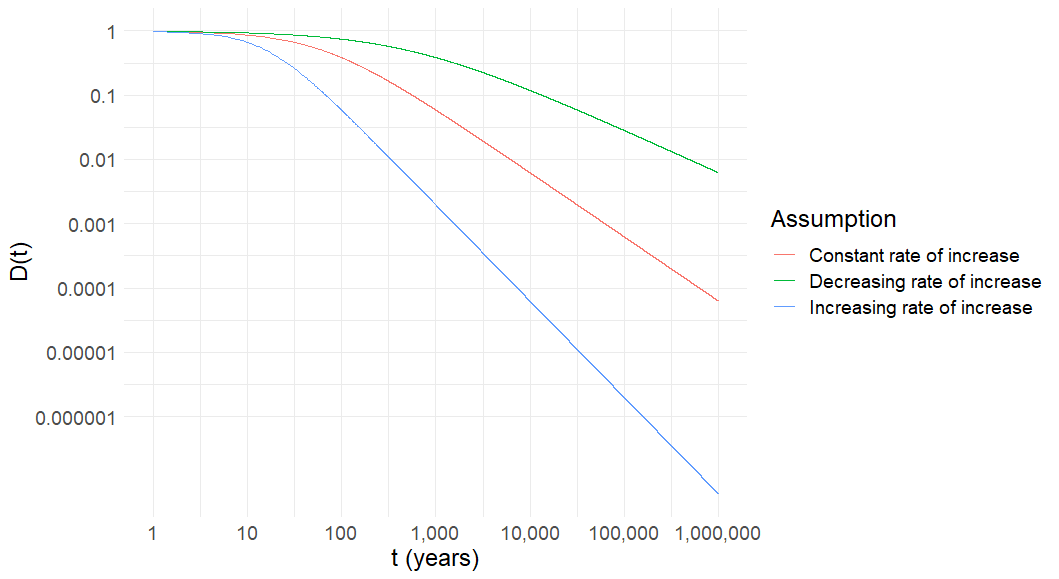
Figure 6 shows how much weight will be put on signals when the noise of the signals evolves in a non-linear fashion (with the linear case in red shown for reference). The weights diverge over time. We can see that around 10,000 years the weight put on the signal with a decreasing rate of signal noise increase is about one order of magnitude greater than the weight put on the constant rate of increase signal. The difference between the constant and increasing rates is even greater, with the increasing rate placing two orders of magnitude less weight on the signal than the constant rate. The 3 order of magnitude difference between the two non-linear cases at 10,000 years is already substantial, and the difference grows with time.
Comparison
Table 4 compares the results of all the previous cases. It shows us, for each case, how long it takes for the posterior expected value to be some fraction of the signal expected value. Again, this is assuming a zero mean, constant variance prior, and a mean 1, but increasing variance signal.
Table 4: How long it takes until posterior expected value is some fraction of signal expected value
Years until posterior expected value is x% of signal | ||||||
|---|---|---|---|---|---|---|
| x% | Central fixed effects | Upper bound, fixed effects | Central, no fixed effects | Upper bound, no fixed effects | Increasing rate of increase | Decreasing rate of increase |
| 10% | 561 | 158 | 187 | 84 | 68 | 13,276 |
| 1% | 6,168 | 1,735 | 2,047 | 923 | 337 | 484,318 |
| 0.1% | 62,233 | 17,507 | 20,651 | 9,307 | 1,571 | 15.5 million |
| 0.01% | 622,886 | 175,218 | 206,690 | 93,144 | 7,294 | 491 million |
We can see that under the preferred central fixed effects estimate, signals of the value produced with a horizon of 561 years produce a posterior expected value that is 10% of the expected value of the signal. Every order of magnitude increase in forecast horizon after that results in a posterior expected value roughly an order of magnitude smaller.
Other than the decreasing rate of increase case, which relied on an arbitrary assumption, the central fixed effects estimate is the one that takes the longest for the posterior expected value to reach a given level. Even given the slow increase in signal noise in this case, the weight put on the signal declines at a moderate speed. You may personally be inclined to put even less weight on long-run signals than these estimates suggest, i.e., you may give signals of the impact of some intervention 561 years into the future much less than 10% of the weight in determining your posterior expected value of that intervention. Nonetheless, even this limited rate of signal noise increase does seem to reduce the posterior long-run value of interventions fairly significantly.
More importantly, though, is the variance across the different cases. There is roughly a 2.5 order of magnitude difference in the number of years it takes for the two non-linear cases to reach a posterior expected value which is 10% of the signal (13,276 to 68). Even restricting our attention to the different linear cases, there is almost an order of magnitude difference between the fastest and the slowest cases (561 to 84).
Please see the appendix for additional robustness checks and the Github repository for the data and code.
There are a number of assumptions made in this work and further work should improve on this by addressing some of the limitations mentioned below.
Limitations
Data
First, we use RCTs that have completed long-run follow-ups. This is clearly a selected subset of RCTs and this selection could bias results. In theory, this could go in either direction, but one plausible story is that the types of RCTs that have long-run follow ups are ones that had larger short-run effects and were expected to have larger long-run effects. This might lead us to do relatively well in predicting the long-run outcomes in this subset and as such underestimate how much predictability declines over time.
Second, we take forecasts on the medium-run impacts of global health and development interventions and generalize them to other domains. You may prefer to use forecasts on questions from a mix of domains or forecasts which are more focused on questions relevant to existential risk and longtermism. These different datasets may produce different results on the relationship between time horizon and forecast noise and the ability of each of them to control for confounding in that relationship varies as well. Other datasets that could be used for this sort of analysis have their own strengths and weaknesses and include:
- Expert forecasts of medium-run RCT impacts (Bernard, 2023)
- Judgemental forecasts of impacts from development economics RCTs
- Iqisa forecasting datasets
- Metaculus
- PredictionBook
- Good Judgement Project
- Open Philanthropy grant predictions
- Forecasts from a mix of cause areas, but typically only one forecast per question
Model assumptions
We make assumptions on both the prior and the signals in the model. In particular, we assume both of them are normally distributed. We assume that the prior is normally distributed around mean 0 with constant variance. We assume that the signals are each normally distributed around the true benefit in that time period with variance that increases with each time period. We discuss each of these characteristics in turn.
Mean zero prior: In the context of this model, the prior is meant to be the agent’s belief about the impact of an intervention before they have seen any information or done any analysis of this intervention. If we select a random intervention the agent could do (whether in the global health and development, animals, or x-risk space) it seems reasonable to assume that its net impact is zero absent any further information. This is in line with the philosophical principle of indifference whereby positive and negative effects are equally likely and the stylised empirical fact that “most social programs don’t work”. We are not saying that your personal prior given your current knowledge of interventions should be mean zero for interventions in any of these spaces; you have likely seen many signals and other evidence in the past that will have already moved your prior away from zero. We use zero for illustrative purposes but it is simple to change it and see how that affects the results (we give an example in the appendix). To be clear, if we’re assuming normally distributed priors and signals, is still the weight you put on the signal and is the weight you put on the prior, regardless of what you assume the expected value of the prior (or the signal) to be. Assuming an expected value of 0 for the mean and 1 for the signal, allows us to additionally interpret as the expected value of the posterior.
If the mean of your prior is closer to the mean of the signal then the posterior expected value won’t be shifted down as much for a given signal. For example, if your signal is mean 1 and your prior and signal have the same variance, then a mean zero prior gives a mean posterior of 0.5, whereas a mean 0.5 prior would give a mean posterior of 0.75. Your prior could also be below zero or above the mean value of the signal.
What your prior actually is depends on your epistemic context. Suppose you’re considering a set of interventions that have already been filtered by someone else for having high expected benefit. Your prior for this set of interventions should likely be greater than zero. However, the person who did the filtering should probably have a prior much closer to 0.
Constant variance prior: We assume that the variance of the prior was the same for each time horizon whereas the variance of the signal increases with time horizon for simplicity. However we might think that the variance of the prior changes with time horizon as well, likely increasing. You might think that in our initial uninformed state, even though we’re uncertain about the short-run benefits of some intervention, we’re even more uncertain about the long-run benefits.
The amount of weight we put on the prior and the signal to form our posterior depends on the relative variance of the two. As we hold the prior variance constant and increase the signal variance, this leads to less weight being put on the signal and more on the prior as time goes on. However, if the variance of the prior grows as well, this doesn’t necessarily have to be the case. If the variance of the prior grows at the same speed as the variance of the signal then the expected value of the posterior will not change with time horizon. If the variance of the prior grows but more slowly than the signal variance, then we will still shrink our posteriors toward the prior, but not as much as in the model above.
Unbiased signal: You might think that signals in some domains consistently over or underestimate the benefits of interventions such that they are biased. Indeed, the original forecasts in the data used did consistently underestimate the benefit of treatment (i.e. they were negatively biased) so we had to correct the forecasts to account for this. However, we were only able to do this because we had the ground truth from the RCTs. If you think signals are biased in some domain, you will have to make a more ad hoc adjustment to them in cases where you don’t have access to the ground truth. However, this adjustment can be done simply by subtracting the bias you expect from the signal (and potentially accounting for the additional uncertainty introduced by your uncertainty over the bias).
Increasing variance signal: This assumption matches the empirical data although the increase in the variance was itself noisily estimated and not statistically significantly different from 0. Furthermore, we take the increase in variance of the signal from a maximum of 20 years of forecast data and extrapolate it indefinitely into the future. We modeled non-linearities in the rate of signal noise increase but had to make assumptions about the shape of the non-linearities. Ultimately, it’s not particularly clear what we should think about the evolution of uncertainty of signals over long time periods, whether it’s increasing or decreasing over time, and a lot more forecast data would be required to properly estimate non-linear relationships here.
Normal distributions: We use normal distributions for mathematical convenience but non-normal distributions with fat tails are everywhere in the real world. The effect on your posterior distribution of using non-normal distributions for your prior or your signal would depend heavily on the exact distributions used and in particular whether they have a heavy positive tail as well as a heavy negative tail. For many x-risk cases, you may also have bimodal priors, for example, if you think AI will either go really well or really badly. The economic modeling would be significantly more challenging when allowing for arbitrary prior and signal distributions and it’s hard to say in advance how this flexibility might affect the conclusions of this report.
Model relevance
You might also think that a model of this style is best targeted for modeling interventions that aim to have persistent long-run effects, whereas the most popular interventions considered by people concerned by long-run effects are existential risk (x-risk) interventions of a different style. Typical x-risk interventions instead aim to in the short-run move us from our current state where we have a moderately high chance of an x-risk, to a stable state where the rates of x-risk are much lower. If you have this concern you might prefer a model more in the style of Tarsney (2022) where he models an exogenous event knocking us out of that stable state. The issue is that empirically estimating the parameters of such a model is a much more challenging task than estimating parameters for the Bayesian updating model used above, and it already required a number of strong assumptions to do the latter.
However, I still think this style of model used above is appropriate for thinking about the long-run value of interventions. Although it doesn’t directly model how we expect x-risk interventions to affect the world, the generality of a stream of value being produced in each period can still capture these sorts of interventions. The x-risk intervention produces value by making it slightly more likely we live in a world that doesn’t face an existential catastrophe relative to the counterfactual where we didn’t do the intervention. The difference between these two worlds is the expected value of the intervention and this can be modeled as a continuous stream of value across time, as in the above model.
Furthermore, we might think another important application of this style of model is about inputs to risks from AI, e.g., increases in compute, dollars spent, performance on capability benchmarks etc. The sort of modeling in this case does not require assumptions about stable states of the world persisting into the future, but instead takes existing data and extrapolates it forward, similarly to the surrogate index data used in this exercise.
Finally, we need to consider how the model reflects standard generation of signals (i.e. evidence or forecasts) in effective altruism. When the signal comes from a purely statistical model like the impact of an RCT that doesn’t rely on priors, as above, then the model applies perfectly. If the signal instead comes from a model that does rely at least to some extent on your priors (for example structural models such as the forthcoming Cross-Cause Cost-Effectiveness Model) then you might be concerned about double counting your prior. If this is the case, you likely should put less weight on the signal (since it is partially determined by and correlated with your priors) than the analysis suggests.
Acknowledgements
This report was written by David Bernard. Thanks to members of the Worldview Investigations Team – Hayley Clatterbuck, Laura Duffy, Bob Fischer, Arvo Muñoz Morán and Derek Shiller – Loren Fryxell, Benjamin Tereick and Duncan Webb for helpful discussions and feedback. The post is a project of Rethink Priorities, a global priority think-and-do tank, aiming to do good at scale. We research and implement pressing opportunities to make the world better. We act upon these opportunities by developing and implementing strategies, projects, and solutions to key issues. We do this work in close partnership with foundations and impact-focused non-profits or other entities. If you're interested in Rethink Priorities' work, please consider subscribing to our newsletter. You can explore our completed public work here.
- ^
Assuming a normal distribution is a simplifying assumption made for the sake of tractability. In the context of the signal being provided by a statistical model which aggregates independent random variables, it is a reasonable assumption due to the central limit theorem.
- ^
See the Development Impact blog for another intuitive explanation.
- ^
By time horizon we mean the gap between when the latest short-run outcome used to make the prediction was observed, and when the long-run outcome being predicted was observed. For example, if we use short-run outcomes from one year after the treatment to predict the ten-year effect, then the time horizon is nine years, whereas if we used data from one and three years after the treatment, the time horizon is seven years.
- ^
The distinction between the Brier Score (BS) and MSE is that the BS is a special case of MSE. In the Brier score, the outcome is an event that either occurs or does not occur so takes either the value 0 or 1, and the forecast is probabilistic; it is about the probability of the event occurring and therefore bounded between 0 and 1 (or 0% and 100%). An example is a forecast of a 35% chance that Donald Trump wins the 2024 presidential election. MSE generally has no constraints on the range of allowable forecasts or outcomes.
- ^
In the context of a Brier Score, unbiased probabilistic forecasts mean that you don’t over or underestimate the overall fraction of events that occur. Note that the assumption of unbiased probabilistic forecasts is weaker than the assumption of perfect calibration. Perfect calibration requires that within each bin the probability of events occurring matches the fraction e.g. for all the 70% forecasts, the events occur 70% of the time on average, and the same is true for every other probability bin. You would still be unbiased overall if you overestimated the likelihood of events in one bin by 10 percentage points and underestimated the likelihood of events in another equally-sized bin by 10 percentage points as these would cancel out. As such, perfect calibration is sufficient for unbiased probabilistic forecasts but not necessary.
- ^
By easiness here I mean to refer to a concept of easiness that is question-specific, separating out from the easiness that comes from the changing forecast horizons.
- ^
See Bernard et al. (2023) for more technical details on the implementation of the meta-analysis.
- ^
I checked whether the error of the uncorrected forecast depends on the forecast horizon by including horizon as a moderator in the meta-regression, but the coefficient on horizon was always small and insignificant.
- ^
Note that the units are different here as the MSE is squared whereas the rule of thumb 0.2 effect size is not. The root mean squared error is more comparable. A mean squared error of 0.2 implies a root mean squared error of 0.44, and it would take 516 years for the root mean squared error to reach this number.
- ^
I estimate this using a meta-analysis as in table 2, but on the true treatment effects themselves, not the error between the true treatment effects and the forecasts.
- ^
I don’t use the lower bounds as these are below 0. Firstly, these would imply negative values of squared errors which are impossible. Secondly, they would imply that long-range forecasts are more accurate than short-range forecasts, which seems implausible. Although the estimated rate of forecast noise increase is small, it seems likely that with more forecast data we would be able to reject the null hypothesis that the rate is 0 or negative.



Great post, David! Probably my favourite of the series so far.
One can think about this along the lines of the inverse-variance weighting. The formula above is equivalent to "expected posterior" = "signal precision"/("prior precision" + "signal precision")*"signal", where "precision" = 1/"variance". This is a particular case (null prior) of Dario Amodei's conclusion that "expected posterior" = ("prior precision"*"prior" + "signal precision"*"signal")/("prior precision" + "signal precision"). As the precision of the signal:
-0.054 is supposed to be -0.047.
I think the rate of increase of the variance of the prior is a crucial consideration. Without any information, I think my actions can have a much greater effect in 10 years that in 10 M years. So I would assume the variance of the prior decreases over time, in which case the signal would be more heavily discounted than in your analysis.
I suspect the posterior expected value may easily be less than 100 years using a prior of decreasing variance, as I think one should do.
If the signal and prior follow a lognormal distribution, their logarithms will follow normal distributions, so I think one can interpret the results of your analysis as applying to the logarithm of the posterior.
Thanks Vasco, I'm glad you enjoyed it! I corrected the typo and your points about inverse-variance weighting and lognormal distributions are well-taken.
I agree that doing more work to specify what our priors should be in this sort of situation is valuable although I'm unsure if it rises to the level of a crucial consideration. Our ability to predict long-run effects has been an important crux for me hence the work I've been doing on it, but in general, it seems to be more of an important consideration for people who lean neartermist than those who lean longtermist.