Summary
- I believe many in the effective altruism community, including me in the past, have at some point concluded that reducing the nearterm risk of human extinction is astronomically cost-effective. For this to hold, it has to increase the chance that the future has an astronomical value, which is what drives its expected value.
- Nevertheless, reducing the nearterm risk of human extinction only obviously makes worlds with close to 0 value less likely. It does not have to make ones with astronomical value significantly more likely. A priori, I would say the probability mass is moved to nearby worlds which are just slightly better than the ones where humans go extinct soon. Consequently, interventions reducing nearterm extinction risk need not be astronomically cost-effective.
- I wonder whether the conclusion that reducing the nearterm risk of human extinction is astronomically cost-effective may be explained by:
- Authority bias, binary bias and scope neglect.
- Little use of empirical evidence and detailed quantitative models to catch the above biases.
Why reducing the nearterm risk of human extinction might be astronomically cost-effective
I believe many in the effective altruism community, including me in the past, have at some point concluded that reducing the nearterm risk of human extinction is astronomically cost-effective. This follows from multiplying:
- A non-negligible reduction in the nearterm risk of human extinction per cost. By nearterm, I mean the next few decades.
- An astronomical expected value of the (longterm) future.
To illustrate, one would get a cost-effectiveness in terms of saving human lives of 3.04*10^39 life/$ (= 2.17*10^-13*1.40*10^52), considering:
- A reduction in the nearterm risk of human extinction of 2.17*10^-13 per dollar, which is the median cost-effectiveness bar for mitigating existential risk I collected.
- The bar does not respect extinction risk, but I assume the people who provided the estimates would have guessed similar values for extinction risk.
- I personally guess human extinction is very unlikely to be an existential catastrophe:
- I estimated a 0.0513 % chance of not fully recovering from a repetition of the last mass extinction 66 M years ago, the Cretaceous–Paleogene extinction event.
- If biological humans go extinct because of advanced AI, I guess it is very likely they will have suitable successors then, either in the form of advanced AI or some combinations between it and humans.
- An expected value of the future of 1.40*10^52 human lives (= (10^54 - 10^23)/ln(10^54/10^23)), which is the mean of a loguniform distribution with minimum and maximum of:
- 10^23 human lives, which is the estimate for “an extremely conservative reader” obtained in Table 3 of Newberry 2021.
- 10^54 lives, which is the largest estimate in Table 1 of Newberry 2021, determined for the case where all the resources of the affectable universe support digital persons. The upper bound can be 10^30 times as high if civilization “aestivate[s] until the far future in order to exploit the low temperature environment”, in which computations are more efficient. Using a higher bound does not qualitatively change my point.
Why it is not?
Firstly, I do not think reducing the nearterm risk of human extinction being astronomically cost-effective implies it is astronomically more cost-effective than interventions not explicitly focussing on tail risk, like ones in global health and development and animal welfare.
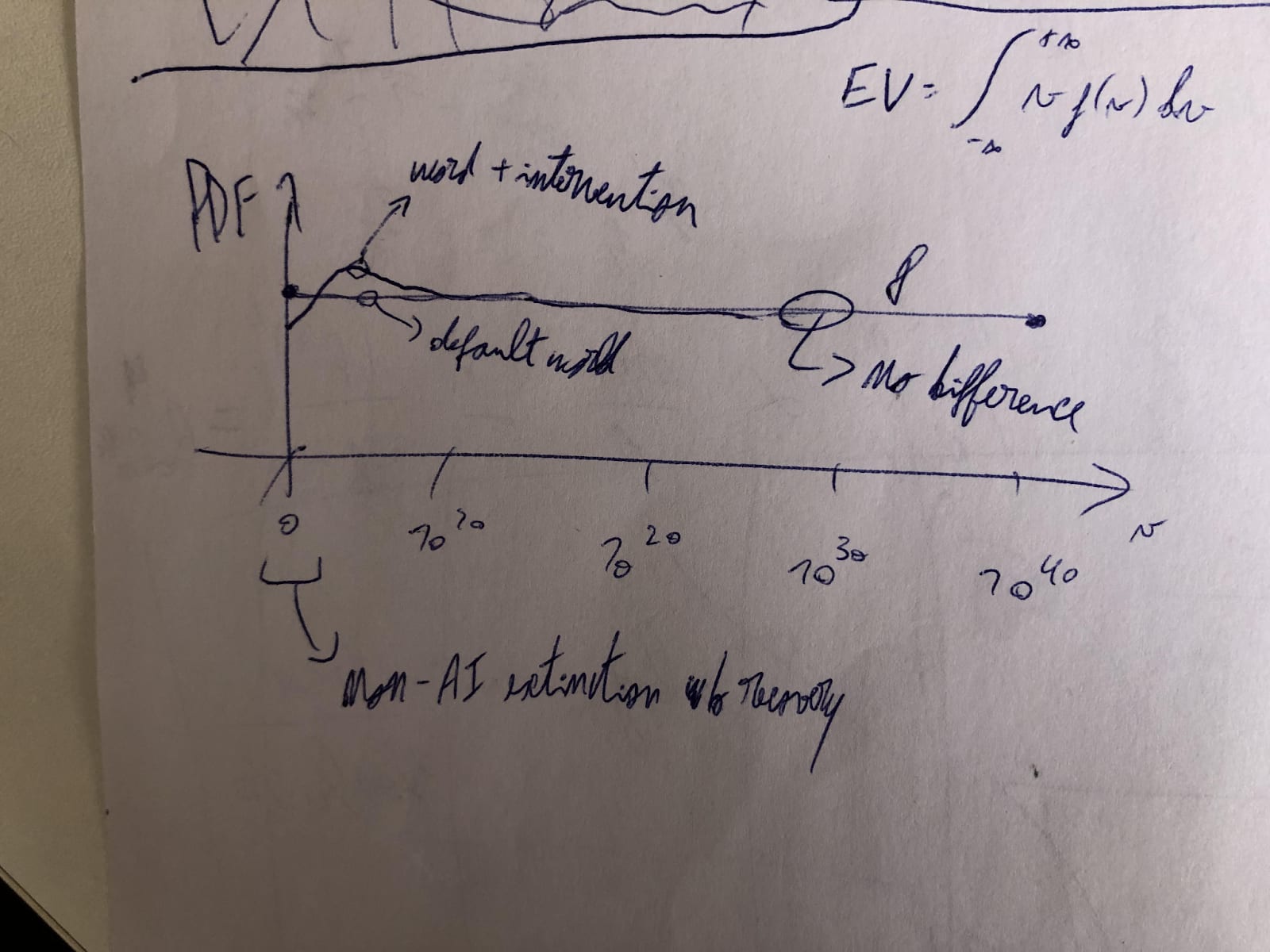
Secondly, and this is what I wanted to discuss here, calculations like the above crucially suppose the reduction in nearterm risk of human extinction is the same as the relative increase in the expected value of the future. For this to hold, reducing such risk has to increase the chance that the future has an astronomical value, which is what drives its expected value. Nevertheless, it only obviously makes worlds with close to 0 value less likely. It does not have to make ones with astronomical value significantly more likely. A priori, I would say the probability mass is moved to nearby worlds which are just slightly better than the ones where humans go extinct soon. Below is my rough sketch of the probability density functions (PDFs) of the value of the future in terms of human lives, before and after an intervention reducing the nearterm risk of human extinction[1].
The expected value (EV) of the future is the integral of the product between the value of the future and its PDF. I assumed the value of the future follows a loguniform distribution from 1 to 10^40 human lives. In the worlds with the least value, humans go extinct soon without the involvement of AI, which has some welfare in expectation, and there is no recovery via the emergence of a similarly intelligent and sentient species[2]. I am also not accounting for wild animals due to the high uncertainty about whether they have positive or negative lives.
In any case, the distribution I sketched does not correspond to my best guess, and I do not think the particular shape matters for the present discussion[3]. What is relevant is that, for all cases, it makes sense to me that an intervention aiming to decrease (increase) the probability of a given set of worlds makes nearby similarly valuable worlds significantly more (less) likely, but super faraway worlds only infinitesimally more (less) so. As far as I can tell, the (posterior) counterfactual impact of interventions whose effects can be accurately measured, like ones in global health and development, decays to 0 as time goes by, and can be modelled as increasing the value of the world for a few years or decades, far from astronomically. Accordingly, I like that Rethink Priorities’ cross-cause cost-effectiveness model (CCM) assumes no counterfactual impact of existential risk interventions after the year of 3023, although I would rather assess interventions based on standard cost-effectiveness analyses.
In light of the above, I expect what David Thorstad calls rapid diminution. I see the difference between the PDF after and before an intervention reducing the nearterm risk of human extinction as quickly decaying to 0, thus making the increase in the expected value of the astronomically valuable worlds negligible. For instance:
- If the difference between the PDF after and before the intervention decays exponentially with the value of the future v, the increase in the value density caused by the intervention will be proportional to v*e^-v[4].
- The above rapidly goes to 0 as v increases. For a value of the future equal to my expected value of 1.40*10^52 human lives, the increase in value density will multiply a factor of 1.40*10^52*e^(-1.40*10^52) = 10^(log10(1.40)*52 - log10(e)*1.40*10^52) = 10^(-6.08*10^51), i.e. it will be basically 0.
The increase in the expected value of the future equals the integral of the increase in value density. As illustrated just above, this increase can easily be negligible for astronomically valuable worlds. Consequently, interventions reducing the nearterm risk of human extinction need not be astronomically cost-effective, and I currently do not think they are.
Intuition pumps
Here are some intuition pumps for why reducing the nearterm risk of human extinction says practically nothing about changes to the expected value of the future. In terms of:
- Human life expectancy:
- I have around 1 life of value left, whereas I calculated an expected value of the future of 1.40*10^52 lives.
- Ensuring the future survives over 1 year, i.e. over 8*10^7 lives (= 8*10^(9 - 2)) for a lifespan of 100 years, is analogous to ensuring I survive over 5.71*10^-45 lives (= 8*10^7/(1.40*10^52)), i.e. over 1.80*10^-35 seconds (= 5.71*10^-45*10^2*365.25*86400).
- Decreasing my risk of death over such an infinitesimal period of time says basically nothing about whether I have significantly extended my life expectancy. In addition, I should be a priori very sceptical about claims that the expected value of my life will be significantly determined over that period (e.g. because my risk of death is concentrated there).
- Similarly, I am guessing decreasing the nearterm risk of human extinction says practically nothing about changes to the expected value of the future. Additionally, I should be a priori very sceptical about claims that the expected value of the future will be significantly determined over the next few decades (e.g. because we are in a time of perils).
- A missing pen:
- If I leave my desk for 10 min, and a pen is missing when I come back, I should not assume the pen is equally likely to be in any 2 points inside a sphere of radius 180 M km (= 10*60*3*10^8) centred on my desk. Assuming the pen is around 180 M km away would be even less valid.
- The probability of the pen being in my home will be much higher than outside it. The probability of being outside Portugal will be negligible, but the probability of being outside Europe even lower, and in Mars even lower still[5].
- Similarly, if an intervention makes the least valuable future worlds less likely, I should not assume the missing probability mass is as likely to be in slightly more valuable worlds as in astronomically valuable worlds. Assuming the probability mass is all moved to the astronomically valuable worlds would be even less valid.
- Moving mass:
- For a given cost/effort, the amount of physical mass one can transfer from one point to another decreases with the distance between them. If the distance is sufficiently large, basically no mass can be transferred.
- Similarly, the probability mass which is transferred from the least valuable worlds to more valuable ones decreases with the distance (in value) between them. If the world is sufficiently faraway (valuable), basically no mass can be transferred.
What do slightly more valuable worlds look like? If the nearterm risk of human extinction refers to the probability of having at least 1 human alive by e.g. 2050, a world slightly more valuable than one where humans go extinct before then would have the last human dying in 2050 instead of 2049, and having a net positive experience during the extra time alive. This is obviously not what people mean by reducing the nearterm risk of human extinction, but it also does not have to imply e.g. leveraging all the energy of the accessible universe to run digital simulations of super happy lives. There are many intermediate outcomes in between, and I expect the probability of the astronomically valuable ones to be increased only infinitesimally.
Similarities with arguments for the existence of God?
One might concede that reducing the nearterm risk of human extinction does not necessarily lead to a meaningful increase in the expected value of the future, but claim that reducing nearterm existential risk does so, because the whole point of existential risk reduction is that it permanently increases the expected value of the future. However, this would be begging the question. To avoid this, one has to present evidence supporting the existence of interventions with permanent effects instead of assuming (the conclusion that) they exist[6], and correspond to the ones designated (e.g. by 80,000 Hours) as decreasing existential risk.
I cannot help notice arguments for reducing the nearterm risk of human extinction being astronomically cost-effective might share some similarities with (supposedly) logical arguments for the existence of God (e.g. Thomas Aquinas’ Five Ways), although they are different in many aspects too. Their conclusions seem to mostly follow from:
- Cognitive biases. In the case of the former, the following come to mind:
- Authority bias. For example, in Existential Risk Prevention as Global Priority, Nick Bostrom interprets a reduction in (total/cumulative) existential risk as a relative increase in the expected value of the future, which is fine, but then deals with the former as being independent from the latter, which I would argue is misguided given the dependence between the value of the future and increase in its PDF. “The more technologically comprehensive estimate of 10^54 human brain-emulation subjective life-years (or 10^52 lives of ordinary length) makes the same point even more starkly. Even if we give this allegedly lower bound on the cumulative output potential of a technologically mature civilisation a mere 1 per cent chance of being correct, we find that the expected value of reducing existential risk by a mere one billionth of one billionth of one percentage point is worth a hundred billion times as much as a billion human lives”.
- Nitpick. The maths just above is not right. Nick meant 10^21 (= 10^(52 - 2 - 2*9 - 2 - 9)) times as much just above, i.e. a thousand billion billion times, not a hundred billion times (10^11).
- Binary bias. This can manifest in assuming the value of the future is not only binary, but also that interventions reducing the nearterm risk of human extinction mostly move probability mass from worlds with value close to 0 to ones which are astronomically valuable, as opposed to just slightly more valuable.
- Scope neglect. I agree the expected value of the future is astronomical, but it is easy to overlook that the increase in the probability of the astronomically valuable worlds driving that expected value can be astronomically low too, thus making the increase in the expected value of the astronomically valuable worlds negligible (see my illustration above).
- Authority bias. For example, in Existential Risk Prevention as Global Priority, Nick Bostrom interprets a reduction in (total/cumulative) existential risk as a relative increase in the expected value of the future, which is fine, but then deals with the former as being independent from the latter, which I would argue is misguided given the dependence between the value of the future and increase in its PDF. “The more technologically comprehensive estimate of 10^54 human brain-emulation subjective life-years (or 10^52 lives of ordinary length) makes the same point even more starkly. Even if we give this allegedly lower bound on the cumulative output potential of a technologically mature civilisation a mere 1 per cent chance of being correct, we find that the expected value of reducing existential risk by a mere one billionth of one billionth of one percentage point is worth a hundred billion times as much as a billion human lives”.
- Little use of empirical evidence and detailed quantitative models to catch the above biases. In the case of the former:
- As far as I know, reductions in the nearterm risk of human extinction as well as its relationship with the relative increase in the expected value of the future are always directly guessed.
Acknowledgements
Thanks to Anonymous Person for a discussion which led me to write this post, and feedback on the draft.
- ^
The area under each curve should be the same (although it is not in my drawing), and equal to 1. In addition, “word + intervention” was supposed to be “world + intervention”.
- ^
I estimated there would only be a 0.0513 % chance of a repetition of the last mass extinction 66 M years ago, the Cretaceous–Paleogene extinction event, being existential.
- ^
As a side note, I have wondered about how binary is the value of the future.
- ^
By value density, I mean the product between the value of the future and its PDF.
- ^
Mars’ aphelion 1.67 AU, and Earth’s is 1.02 AU, so Mars can be as much as 2.69 AU (= 1.67 + 1.02) away from Earth. This is more than the 1.20 AU (= 1.80*10^11/(1.50*10^11)) which the pen could have travelled at the speed of light. Consequently, the probability of it being in Mars could be as low as exactly 0 conditional on it not having travelled faster than light.
- ^
As Toby Ord does in his framework for assessing changes to humanity’s longterm trajectory.
- ^
Speculative side note. In theory, scope neglect might be a little explained by more extreme events being less likely. People may value a gain in welfare of 100 less than 100 times a gain of 1 because deep down they know the former is much less likely, and then fail to adequately account for the conditions of thought experiments where both deals are supposed to be equally likely. For a loguniform distribution, the value density does not depend on the value. For a Pareto distribution, it decreases with value, which could explain higher gains sometimes being valued less.
Here's a framing which I think captures some (certainly not all) of what you're saying. Imagine graphing out percentiles for your credence distribution over values the entire future can take. We can consider the effect that extinction mitigation has on the overall distribution, and the change in expected value which the mitigation has. In the diagrams below, the shaded area represents the difference made by extinction migitation.
The closest thing to a ‘classic’ story in my head looks like below: on which (i) the long-run future is basically biomodal, between ruin and near-best futures, and (ii) the main effect of extinction mitigation is to make near-best futures more likely.
A rough analogy: you are a healthy and othrewise cautious 22-year old, but you find yourself trapped on a desert island. You know the only means of survival is a perilous week-long journey on your life raft to the nearest port, but you think there is a good chance you don't survive the journey. Supposing you make the journey alive, then your distribution over your expected lifespan from this point (ignoring the possibility of natural lifespan enhancement) basically just shifts to the left as above (though with negligible weight on living <1 year from now).
A possibility you raise is that the main effect of preventing extinction is only to make worlds more likely which are already close to zero value, as below.
A variant on this possibility is that, if you knew some option to prevent human extinction were to be taken, your new distribution would place less weight on near-zero futures, but less weight on the best futures also. So your intervention affects many percentiles of your distribution, in a way which could make the net effect unclear.
One reason might be causal: the means required to prevent extinction might themselves seal off the best futures. In a variant of the shipwreck example, you could imagine facing the choice between making the perilous week-long journey, or waiting it out for a ship to find you in 2 months. Suppose you were confident that, if you wait it out, you will be found alive, but at the cost of reducing your overall life expectancy (maybe because of long-run health effects).
The above possibilities (i) assume that your distribution over the value of the future is roughly bimodal, and (ii) ignore worse-than-zero outcomes. If we instead assume a smooth distribution, and include some possibility of worse-than-zero worlds, we can ask what effect mitigating extinction has.
Here's one possibility: the fraction of your distribution that effectively zero value worlds gets is ‘pinched’, giving more weight both to better-than-zero worlds, and worse-than-zero worlds. Here you'd need to explain why this is a good thing to do.
So an obvious question here is how likely it is that extinction mitigation is more like the ‘knife-edge’ scenario of a healthy person trapped in a survive-or-die predicament. I agree that the ‘classic’ picture of the value of extinction mitigation can mislead about how obvious this is for a bunch of reasons. Though (as other commenters seem to have pointed out) it's unclear how much to rely on relatively uninformed priors, versus the predicament we seem to find ourselves in when we look at the world.
I'll also add that, in the case of AI risk, I think that framing literal human extinction as the main test of whether the future will be good seems like a mistake, in particular because I think literal human extinction is much less likely than worlds where things go badly for other reasons.
Curious for thoughts, and caveat that I read this post quickly and mostly haven't read the comments.
Thanks for the comment, Fin! Strongly upvoted.
I personally find it more intuitive to plot the PDF of the value of the future, instead of its cumulative distribution function as you did, but I like your graphs too!
I do not know whether the value of the future is bimodal. However, even if so, I would guess reducing the nearterm risk of human extinction only infinitesimaly increases the probability of astronomically valuable worlds. Below is an illustration. The normal and dashed lines are the PDFs of the value of the future before and after the intervention. I suppose the neutral worlds would be made slightly less likely (dashed line below the normal line), and the slightly negative and positive worlds would me made slightly more likely (dashed line above the normal line), but the astronomically negative and positive worlds would only be made infinitesimaly more likely (basically no difference between the normal and dashed line).
Are there any interventions whose estimates of (posterior) counterfactual impact, in terms of expected total hedonistic utility (not e.g. preventing the extinction of a random species), do not decay to 0 in at most a few centuries? From my perspective, their absence establishes a strong prior against persistent longterm effects.
I wonder whether the probability of things going badly is proportional to the nearterm risk of human extinction. In any case, I am not sure the size of the risk affects the possibility of some interventions having astronomical cost-effectiveness. I guess this mainly depends on how fast the (posterior) counterfactual impact decreases with the value of the future. If exponentially, based on my Fermi estimate in the post, the counterfactual impact linked to making astronomically valuable worlds more likely will arguably be negligible.
I would be curious to know how low would the risk of human extinction in the next 10 years (or other period) have to be for you to mostly:
(In response to a request for thoughts from Vasco:)
Honestly I don't really like "astronomically cost-effective" framings; I think they're misleading, because they imply too much equivalence with standard cost-effectiveness analysis, whereas if they're taken seriously then it's probably the case that many many actions have astronomical expected impact.
However, I think I largely disagree with what you're saying here. I'll respond to a couple of points in particular:
Thanks for the comment, Owen!
Agreed[1].
You kind of anticipated my reply with your last point. Once I condition on a given human dying in the next e.g. 1.80*10^-35 seconds (calculation in the post), I should expect there is an astronomically high cost of extending the life expectancy to the baseline e.g. 100 years (e.g. because it is super hard to avoid simulation shutdown or vacuum decay). With reasonable costs, I would only be able to increase it infinitesimaly (e.g. by moving a few kilometers away from the location from which the universal collapse wave comes).
Agreed.
I know you italicised "all", but, just to clarify, I do not think all the probability mass would go to such worlds. Some non-negligible mass would go to astronomically valuable worlds, but I think it would be so small that the increase in the expected the value of these would be negligible. Do you have a preferred function describing the difference between the PDF of the value of the future after and before the intervention? It is unclear to me why assuming a decaying exponential, as I did in my calculations for illustration, would be wild.
I sort of take branch 2. I agree eliminating a 1 % instantaneous risk of the universe collapsing would have astronomical benefits, but I would say it would be basically impossible. I think the cost/difficulty of eliminating a risk tends to infinity as the duration of the risk tends to 0[2], in which case the cost-effectiveness of mitigating the risk also goes to 0. In addition, eliminating a risk becomes harder as its potential impact increases, such that eliminating a risk which endargers the whole universe is astronomically harder than eliminating one that only endangers humans.
As the duration and scope of the risk decreases, postulating that the relative increase in the expected value of the future matches the (absolute) reduction in risk becomes increasingly less valid.
Describing a risk as binary as in your example[3], it is more natural to assume that the probability mass which is taken out of the risk is e.g. loguniformly distributed across all the other worlds, thus meaningully increasing the chance of astronomically valuable worlds, and resulting in risk mitigation being astronomically cost-effective. However, describing a risk as continous (in time and scope), it is more natural to suppose that the change in its duration and impact will be continuous, and this does not obviously result in risk mitigation being astronomically cost-effective.
On 1, I guess the probability of humans going extinct over the next 10 years is 10^-7, so nowhere near as small as needed to result in non-astronomically large cost-effectiveness when multiplied by the expected value of the future. However, you are right this is not the main point of the post.
On 3, I guess you find a non-astronomical expected value of the future more plausible due to your guess for the nearterm risk of human extinction being orders of magnitude higher than mine.
I say in the post that:
In general, any task (e.g. risk mitigation) can be made arbitrarily costly/hard by decreasing the time in which it has to be performed. At the limit, the task becomes impossible when there is no time to complete it.
Either it is on or off. Either it affects the whole universe or nothing at all.
Trying to aim at the point of most confusion about why we're seeing things differently:
Why doesn't your argument show that medical intervention during birth can have only a negligible effect on life expectancy?
For the situation to be analogous, one would have to consider an intervention decreasing the risk of a death over 1.80*10^-35 seconds (see calculations in the post), in which case it does feel intuitive to me that changing the life expectancy would be quite hard. Either the risk would occur over a much longer period, and therefore the intervention would only be mitigating a minor fraction of it, or it would be a very binary risk like simulation shutdown that would be super hardly be reduced.
Of course it's not intended to be a strict analogy. Rather, I take the whole shape of your argument to be a strong presumption against interventions during a short period X having an expected effect on total lifespan that is >>X.
But I claim that this happens with birth. Birth is something like 0.0001% of the duration of the whole life, but interventions during birth can easily have impacts on life expectancy which are much greater than 0.0001%. Clearly there's some mechanism in operation here which means these don't need to be tightly coupled. What is it, and why doesn't it apply to the case of extinction risk?
Obviously the numbers involved are much more extreme in the case of human extinction, but I think the birth:life duration ratio is already big enough that we could hope to learn useful lessons from that.
Thanks for clarifying. My argument depends on the specific numbers involved. Reducing the risk of human extinction over the next year only directly affects around 10^10 lives, i.e. 10^-43 (= 10^(9 - 52)) of my estimate for the expected value of the future. I see such reduction as astronomically harder than decreasing a risk which only directly affect 10^-6 (= 0.0001 %) of the value. My main issue is that these arguments are often analysed informally, whereas I think they require looking into maths like how fast the tail of counterfactual effects decays. I have now added the following bullets to the post, which were initially not imported:
Sorry, I don't find this is really speaking to my question?
I totally believe that people make mistakes in thinking about this stuff for reasons along the lines of the biases you discuss. But I also think that you're making some strong assumptions about things essentially cancelling out that I think are unjustified, and talking about mistakes that other people are making doesn't (it seems to me) work as a justification.
I do not think the difficulty of decreasing a risk is independent of the value at stake. It is harder to decrease a risk when a larger value is at stake. So, in my mind, decreasing the nearterm risk of human extinction is astronomically easier than decreasing the risk of not achieving 10^50 lives of value, such that decreasing the former by e.g. 10^-10 leads to a relative increase in the latter much smaller than 10^-10.
Could you elaborate on why you think I am making a strong assumption in terms of questioning the following?
Do you think I am overestimating how fast the difference between the PDF after and before the intervention decays? As far as I can tell, the (posterior) counterfactual impact of interventions whose effects can be accurately measured, like ones in global health and development, decays to 0 as time goes by. I do not have a strong view on the particular shape of the difference, but exponential decay is quite typical in many contexts.
This makes sense as a kind of general prior to come in with. Although note:
Now it looks to me as though you're dogmatically sticking with the prior. Having come across the (kinda striking) observation which says "if there's a realistic chance of spreading to the stars, then premature human extinction would forgo astronomical value", it seems like you're saying "well that would mean that the prior was wrong, so that observation can't be quite right", and then reasoning from your prior to try to draw conclusions about the causal relationships there.
Whereas I feel that the prior reasonably justifies more scepticism in cases where more lives are at stake (and indeed, I do put a bunch of probability on "averting near-term extinction doesn't save astronomical value for some reason or another", though the reasons tend to be ones where we never actually had a shot of an astronomically big future in the first place, and I think that that's sort of the appropriate target for scepticism), but doesn't give you anything strong enough to be confident about things.
(I certainly wouldn't be surprised if I'm somehow misunderstanding what you're doing; I'm just responding to the picture I'm getting from what you've written.)
Are there any interventions whose estimates of (posterior) counterfactual impact do not decay to 0 in at most a few centuries? From my perspective, their absence establishes a strong prior against persistent longterm effects.
This makes a lot of sense to me too.
In general our ability to measure long term effects is kind of lousy. But if I wanted to look for interventions which don't have that decay pattern it would be most natural to think of conservation work saving species from extinction. Once we've lost biodiversity, it's essentially gone (maybe taking millions of years to build up again naturally). Conservation work can stop that. And with rises in conservation work over time it's quite plausible that early saving species won't just lead to them going extinct slightly later, but being preserved indefinitely.
I was not clear above, but I meant (posterior) counterfactual impact under expected total hedonistic utilitarianism. Even if a species is counterfactually preserved indefinitely due to actions now, which I think would be very hard, I do not see how it would permanently increase wellbeing. In addition, I meant to ask for actual empirical evidence as opposed to hypothetical examples (e.g. of one species being saved and making an immortal conservationist happy indefinitely).
I think this is something where our ability to measure is just pretty bad, and in particular our ability to empirically detect whether the type of things that plausibly have long lasting counterfactual impacts actually do is pretty terrible.
I respond to that by saying "ok I guess empirics aren't super helpful for the big picture question let's try to build mechanistic understanding of things grounded wherever possible in empirics, as well as priors about what types of distributions occur when various different generating mechanisms are at play", whereas it sounds like you're responding by saying something like "well as a prior we'll just use the parts of the distribution we can actually measure, and assume that generalizes unless we get contradictory data"?
Yes, that would be my reply. Thanks for clarifying.
Yeah, so I basically think that that response feels "spiritually frequentist", and is more likely to lead you to large errors than the approach I outlined (which feels more "spiritually Bayesian"), especially in cases like this where we're trying to extrapolate significantly beyond the data we've been able to gather.
I disagree. One way of looking at it:
Imagine many, many civilizations that are roughly as technologically advanced as present-day human civilization.
Claim 1: Some of them will wind up having astronomical value (at least according to their own values)
Claim 2: Of those civilizations that do wind up having astronomical value, some will have gone through near misses, or high-risk periods, when they could have gone extinct if things had worked out slightly differently
Claim 3: Of those civilizations that do go extinct, some would have had wound up having astronomical value if they had survived that one extinction event. These are civilizations much like the ones in claim 2, but who got hit instead of getting a near miss.
Claim 4: Given claims 1-3, and that the "some" civilizations described in claims 1-3 are not vanishingly rare (enough to balance out the very high value), the expected value of averting a random extinction event for a technologically advanced civilization is astronomically high.
Then to apply this to humanity, we need something like:
Claim 5: We don't have sufficient information to exclude present-day humanity from being one of the civilizations from claim 1 which winds up having astronomical value (or at least humanity conditional on successfully navigating the transition to superintelligent AI and surviving the next century in control of its own destiny)
Do you have much reason to believe Claim 1 is true? I would've thought that's where most people's intuitions differ, though maybe not Vasco's specific crux.
Hi Linch,
I think what mostly matters is how fast the difference between the PDF of the value of the future after and before an intervention decays with the value of the future, not the expected value of the future.
Thanks for the comment, Dan.
I think such civilisations are indeed vanishingly rare. The argument you are making is the classical type of argument I used to endorse, but no longer do. As the one Nick Bostrom makes in Existential Risk Prevention as Global Priority (see my post), it is scope sensitive to the astronomical expected value of the future, but scope insensitive to the infinitesimal increase in probability of astronomically valuable worlds, which results in an astronomical cost of moving probability mass from the least valuable worlds to astronomically valuable ones. Consequently, interventions reducing the nearterm risk of human extinction need not be astronomically cost-effective, and I currently do not think they are.
10^-35 is such a short period of time that basically nothing can happen during it - even a laser couldn't cut through your body that quickly. But it seems intuitive to me that ensuring someone survives the next one second, if they would otherwise be hit by a bullet during that one second, could dramatically increase their life expectancy.
To explicitly do the calculation, lets assume a handgun bullet hits someone at around ~250m/s, and decelerates somewhat, taking around 10^-3 seconds to pass through them. Assuming they were otherwise a normal person who didn't often get shot at, intervening to protect them for ~10^-3 seconds would give them about 50 years ~= 10^9 seconds of extra life, or 12 orders of magnitude of leverage.
This example seems analogous to me because I believe that transformative AI basically is a one-time bullet and if we can catch it in our teeth we only need to do so once.
Thanks for engaging, Larks!
Right, even in a vacuum, light takes 10^-9 s (= 0.3/(3*10^8)) to travel 30 cm.
I do not think your example is structurally analogous to mine:
The mean person who is 10^-3 away from being killed, who has e.g. a bullet 25 cm (= 250*10^-3) away from the head if it is travelling at 250 m/s, presumably has a very short life expectancy. If one thinks humanity is in a similar situation with respecto to AI, then the expected value of the future is also arguably not astronomical, and therefore decreasing the nearterm risk of human extinction need not be astronomically cost-effective. Pushing the analogy to an extreme, decreasing deaths from shootings is not the most effective way to extend human life expectancy.
I think I agree with the title, but not with the argument you've made here.
If you believe that the future currently has astronomical expected value, then a non-tiny reduction in nearterm extinction risk must have astronomical expected value too.
Call the expected value conditional on us making it through the next year, U.
If you believe future has astronomical expected value, then U must be astronomically large.
Call the chance of extinction in the next year, p.
The expected value contained >1 year in the future is:
p * 0 + (1-p) * U
So if you reduce p by an amount dp, the change in expected value >1 year in the future is:
U * dp
So if U is astronomically big, and dp is not astronomically small, then the expected value of reducing nearterm extinction risk must be astronomically big as well.
The impact of nearterm extinction risk on future expected value doesn't need to be 'directly guessed', as I think you are suggesting? The relationship can be worked out precisely. It is given by the above formula (as long as you have an estimate of U to begin with).
This is similar to the conversation we had on the Toby Ord post, but have only just properly read your post here (been on my to-read list for a while!)
I actually agree that reducing near-term extinction risk is probably not astronomically cost-effective. But I would say this is because U is not astronomically big in the first place, which seems different to the argument you are making here.
Thanks for looking into the post, Toby!
I used to think along the lines you described, but I believe I was wrong.
One can simply consider these 2 outcomes, but I find it more informative to consider many potential futures, and how an intervention changes the probability of each of them. I posted a comment about how I think this would work out for a binary future. To illustrate, assume there are 101 possible futures with value U_i = 10^i - 1 (for i between 0 and 100), and that future 0 corresponds to human extinction in 2025 (U_0 = 0). The increase in expected values equals to Delta = sum_i dp_i*U_i, where dp_i is the variation in the probability of future i (sum_i dp_i = 0).
Decreasing the probability of human extinction over 2025 by 100 % does not imply Delta is astronomically large. For example, all the probability mass of future 0 could be moved to future 1 (dp_1 = -dp_0, and dp_i = 0 for i between 2 to 100). In this case, Delta = 9*|dp_0| would be at most 9 (dp_i <= 1), i.e. far from astronomically large.
For Delta to be astronomically large, non-negligible probability mass has to be moved from future 0 to astronomically valuable futures. dp = sum_(i >= 1) dp_i not being astronomically small is not enough for that. I think the easiest way to avoid human extinction in 2025 is postponing it to 2026, which would not make the future astronomically valuable.
I agree the impact of decreasing the nearterm risk of human extinction does not have to be directly guessed. I just meant it has traditionally been guessed. In any case, I think one had better use standard cost-effectiveness analyses.
Thanks for the explanation, I have a clearer understanding of what you are arguing for now! Sorry I didn't appreciate this properly when reading the post.
So you're claiming that if we intervene to reduce the probability of extinction in 2025, then that increases the probability of extinction in 2026, 2027, etc, even after conditioning on not going extinct earlier? The increase is such that the chance of reaching the far future is unchanged?
My next question is: why should we expect something like that to be true???
It seems very unlikely to me that reducing near term extinction risk in 2025 then increases P(extinction in 2026 | not going extinct in 2025). If anything, my prior expectation is that the opposite would be true. If we get better at mitigating existential risks in 2025, why would we expect that to make us worse at mitigating them in 2026?
If I understand right, you're basing this on a claim that we should expect the impact of any intervention to decay exponentially as we go further and further into the future, and you're then looking at what has to happen in order to make this true. I can sympathise with the intuition here. But I don't agree with how it's being applied.
I think the correct way of applying this intuition is to say that it's these quantities which will only be changed negligibly in the far future by interventions we take today:
P(going extinct in far future year X | we reach far future year X) (1)
E(utility in far future year X | we reach year X) (2)
In a world where the future has astronomical value, we obviously can astronomically change the expected value of the future by adjusting near-term extinction risk. To take an extreme example: if we make near-term extinction risk 100%, then expected future value becomes zero, however far into the future X is.
I think asserting that (1) and (2) are unchanged is the correct way of capturing the idea that the effect of interventions tends to wash out over time. That then leads to the conclusion from my original comment.
I think your life-expectancy example is helpful. But I think the conclusion is the opposite of what you're claiming. If I play Russian Roulette and take an instantaneous risk of death, p, and my current life expectancy is L, then my life expectancy will decrease by pL. This is certainly non-negligible for non-negligible p, even though the time I take the risk over is minuscule in comparison to the duration of my life.
Of course I have changed your example here. You were talking about reducing the risk of death in a minuscule time period, rather than increasing it. It's true that that doesn't meaningfully change your life expectancy, but that's not because the duration of time is small in relation to your life, it's because the risk of death in such a minuscule time period is already minuscule!
If we translate this back to existential risk, it does become a good argument against the astronomical cost-effectiveness claim, but it's now a different argument. It's not that near-term extinction isn't important for someone who thinks the future has astronomical value. It's that: if you believe the future has astronomical value, then you are committed to believing that the extinction risk in most centuries is astronomically low, in which case interventions to reduce it stop looking so attractive. The only way to rescue the 'astronomical cost-effectiveness claim' is to argue for something like the 'time of perils' hypothesis. Essentially that we are doing the equivalent of playing Russian Roulette right now, but that we will stop doing so soon, if we survive.
No worries; you are welcome!
Yes, I think so.
It is not that I expect us to get worse at mitigation. I just expect it is way easier to move probability mass from the words with human extinction in 2025 to the ones with human extinction in 2026 than to ones with astronomically large value. The cost of moving physical mass increases with distance, and I guess the cost of moving probability mass increases (maybe exponentially) with value-distance (difference between the value of the worlds).
Yes.
Correct me if I am wrong, but I think you are suggesting something like the following. If there is a 99 % chance we are in future 100 (U_100 = 10^100), and a 1 % (= 1 - 0.99) chance we are in future 0 (U_0 = 0), i.e. if it is very likely we are in an astronomically valuable world[1], we can astronomically increase the expected value of the future by decreasing the chance of future 0. I do not agree. Even if the chance of future 0 is decreased by 100 %, I would say all its probability mass (1 pp) would be moved to nearby worlds whose value is not astronomical. For example, the expected value of the future would only increase by 0.09 (= 0.01*9) if all the probability mass was moved to future 1 (U_1 = 9).
The time of perils hypothesis implies the probability mass is mostly distributed across worlds with tiny and astronomical value. However, the conclusion I reached above does not depend on the initial probabilities of futures 0 and 100. It works just as well for a probability of future 0 of 50 %, and a probability of future 100 of 50 %. My conclusion only depends on my assumption that decreasing the probability of future 0 overwhelmingly increases the chance of nearby non-astronomically valuable worlds, having a negligible effect on the probability of astronomically valuable worlds.
If there was a 100 % of us being in an astronomically valuable world, there would be no nearterm extinction risk to be decreased.
The claim you quoted here was a lot simpler than this.
I was just pointing out that if we take an action to increase near-term extinction risk to 100% (i.e. we deliberately go extinct), then we reduce the expected value of the future to zero. That's an undeniable way that a change to near-term extinction risk can have an astronomical effect on the expected value of the future, provided only that the future has astronomical expected value before we make the intervention.
But this is more or less a consequence of your claims isn't it?
I don't see any basis for this assumption. For example, it is contradicted by my example above, where we deliberately go extinct, and therefore move all of the probability weight from U_100 to U_0, despite their huge value difference.
Or I suppose maybe I do agree with your assumption (as can't think of any counter-examples I would actually endorse in practice) I just disagree with how you're explaining its consequences. I would say it means the future does not have astronomical expected value, not that it does have astronomical value but that we can't influence it (since it seems clear we can if it does).
(If I remember our exchange on the Toby Ord post correctly, I think you made some claim along the lines of: there are no conceivable interventions which would allow us to increase extinction risk to ~100%. This seems like an unlikely claim to me, but it's also I think a different argument to the one you're making in this post anyway.)
Here's another way of explaining it. In this case the probability p_100 of U_100 is given by the huge product:
P(making it through next year) X P(making it through the year after given we make it through year 1) X ........ etc
Changing near-term extinction risk is influencing the first factor in this product, so it would be weird if it didn't change p_100 as well. The same logic doesn't apply to the global health interventions that you're citing as an analogy, and makes existential risk special.
In fact I would say it is your claim (that the later factors get modified too in just such a special way as to cancel out the drop in the first factor) which involves near-term interventions having implausible effects on the future that we shouldn't a priori expect them to have.
Agreed. However, I would argue that increasing the nearterm risk of human extinction to 100 % would be astronomically difficult/costly. In the framework of my previous comment, that would eventually require moving probability mass from world 100 to 0, which I believe is as super hard as moving mass world 0 to 100.
One can make a similar argument for the effect size of global health and development interventions. Assuming the effect size is strictly decreasing, denoting by Xi the effect size at year i, P(XN>x)=P(X1>x)P(X2>x|X1>x)...P(XN>x|XN−1>x). Ok, P(XN>x) increases with P(X1>x) on priors. However, it could still be the case that the effect size will decay to practically 0 within a few decades or centuries.
I don't see why the same argument holds for global health interventions....?
Why should X_N > x require X_1 > x....?
It is not a strict requirement, but it is an arguably reasonable assumption. Are there any interventions whose estimates of (posterior) counterfactual impact, in terms of expected total hedonistic utility (not e.g. preventing the extinction of a random species), do not decay to 0 in at most a few centuries? From my perspective, their absence establishes a strong prior against persistent/increasing effects.
Sure, but once you've assumed that already, you don't need to rely any more on an argument about shifts to P(X_1 > x) being cancelled out by shifts to P(X_n > x) for larger n (which if I understand correctly is the argument you're making about existential risk).
If P(X_N > x) is very small to begin with for some large N, then it will stay small, even if we adjust P(X_1 > x) by a lot (we can't make it bigger than 1!) So we can safely say under your assumption that adjusting the P(X_1 > x) factor by a large amount does influence P(X_N > x) as well, it's just that it can't make it not small.
The existential risk set-up is fundamentally different. We are assuming the future has astronomical value to begin with, before we intervene. That now means non-tiny changes to P(Making it through the next year) must have astronomical value too (unless there is some weird conspiracy among the probability of making it through later years which precisely cancels this out, but that seems very weird, and not something you can justify by pointing to global health as an analogy).
Thanks for the discussion, Toby. I do not plan to follow up further, but, for reference/transparency, I maintain my guess that the future is astronomically valuable, but that no interventions are astronomically cost-effective.
Thanks for the post, Vasco!
From reading your post, your main claim seems to be: The expected value of the long-term future is similar whether it's controlled by humans, unaligned AGI, or another Earth-originating intelligent species.
If that's a correct understanding, I'd be interested in a more vigorous justification of that claim. Some counterarguments:
You also dispute that we're living in a time of perils, though that doesn't seem so cruxy, since your main claim above should be enough for your argument to go through either way. Still, your justification is that "I should be a priori very sceptical about claims that the expected value of the future will be significantly determined over the next few decades". There's a lot of literature (The Precipice, The Most Important Century, etc) which argues that we have enough evidence of this century's uniqueness to overcome this prior. I'd be curious about your take on that.
(Separately, I think you had more to write after the sentence "Their conclusions seem to mostly follow from:" in your post's final section?)
Thanks for the comment, Ariel!
I did not intend to make that claim, and I do not have strong views about it. My main claim is the 2nd bullet of the summary. Sorry for the lack of clarity. I appreciate I am not making a very clear/formal argument, although I think the effects I am pointing to are quite important. Namely, that the probability of increasing the value of the future by a given amount is not independent of that amount.
I do not think we are in a time of perils, in the sense I would say the annual risk of human extinction has generally been going down until now, although with some noise[1]. A typical mammal species has a lifespan of 1 M years, which suggests an annual risk of going extinct of 10^-6. I have estimated values much lower than that. 5.93*10^-12 for nuclear wars, 2.20*10^-14 for asteroids and comets, 3.38*10^-14 for supervolcanoes, a prior of 6.36*10^-14 for wars, and a prior of 4.35*10^-15 for terrorist attacks. My actual best guess for the risk of human extinction over the next 10 years is 10^-7, i.e. around 10^-8 per year. However, besides this still being lower than 10^-6, it is driven by the risk from advanced AI which I assume has some moral value (even now), so the situation would not be analogous.
Thanks for noting that! I have now added the bullets following that sentence, which were initially not imported (maybe they add a little bit of clarity to the post):
Even from the start of World War 2 in 1939 to when nuclear warheads peaked in 1986, the fraction of people living in democracies increased 21.6 pp (= 0.156 + 0.183 - (0.0400 + 0.0833)).
only skimmed your post so not sure if helpful but I wrote this a while ago. https://forum.effectivealtruism.org/posts/zLi3MbMCTtCv9ttyz/formalizing-extinction-risk-reduction-vs-longtermism
Also you might find this helpful
https://forum.effectivealtruism.org/posts/zuQeTaqrjveSiSMYo/a-proposed-hierarchy-of-longtermist-concepts
I discussed this post with @Ryan Greenblatt.