Introduction

When a system is made safer, its users may be willing to offset at least some of the safety improvement by using it more dangerously. A seminal example is that, according to Peltzman (1975), drivers largely compensated for improvements in car safety at the time by driving more dangerously. The phenomenon in general is therefore sometimes known as the “Peltzman Effect”, though it is more often known as “risk compensation”.^[1] One domain in which risk compensation has been studied relatively carefully is NASCAR (Sobel and Nesbit, 2007; Pope and Tollison, 2010), where, apparently, the evidence for a large compensation effect is especially strong.^[2]

In principle, more dangerous usage can partially, fully, or more than fully offset the extent to which the system has been made safer holding usage fixed. Making a system safer thus has an ambiguous effect on the probability of an accident, after its users change their behavior.

There’s no reason why risk compensation shouldn’t apply in the existential risk domain, and we arguably have examples in which it has. For example, reinforcement learning from human feedback (RLHF) makes AI more reliable, all else equal; so it may be making some AI labs comfortable releasing more capable, and so maybe more dangerous, models than they would release otherwise.^[3]

Yet risk compensation per se appears to have gotten relatively little formal, public attention in the existential risk community so far. There has been informal discussion of the issue: e.g. risk compensation in the AI risk domain is discussed by Guest et al. (2023), who call it “the dangerous valley problem”. There is also a cluster of papers and works in progress by Robert Trager, Allan Dafoe, Nick Emery-Xu, Mckay Jensen, and others, including these two and some not yet public but largely summarized here, exploring the issue formally in models with multiple competing firms. In a sense what they do goes well beyond this post, but as far as I’m aware none of their work dwells on what drives the logic of risk compensation even when there is only one firm, and it isn’t designed to build intuition as simply as possible about when it should be expected to be a large or a small effect in general.

So the goal of this post is to do that, using x-risk from AI as the running example. The post is about risk compensation in general, not about AI risk, and I don’t know whether risk compensation should be expected to be a large or small effect in the AI domain (or any other), but hopefully having an example in mind makes it easier to follow the reasoning and decide how large you expect risk compensation effects to be in a given domain you’re familiar with. The post also introduces some distinctly “economic” intuitions around risk compensation which I found helpful and have not quite seen spelled out before (though they don’t differ much in spirit from Appendix B of Peltzman’s original paper).

Model

An AI lab’s preferences

In this model, a deployed AI system either immediately causes an existential catastrophe or is safe. If it’s safe, it increases the utility of the lab that deployed it. Referring to the event that it turns out to be safe as “survival”, the expected utility of the lab is the product of two terms:

      ${\text{EU}}_{\text{lab}}$ = (the probability of survival) ⨉ (the lab’s utility given survival).

That is, without loss of generality, the lab’s utility level in the event of the catastrophe is denoted 0. Both terms are functions of two variables:

• some index of the resources invested in safety work, denoted $S\ge 0$ (“safety work”), and
• some index of how capable the AI is and/or how widely it’s deployed, denoted $C\ge 0$ (“capabilities”).

Utility given survival

Starting with the second term: we will say that the lab’s utility given survival $U\left(C\right)$
a1. increases continuously and unboundedly in $C$ and
a2. is independent of $S$. That is, given that survival was achieved, the lab does not care intrinsically about how much effort was put into safety.

Under these assumptions, we can posit, without loss of generality, that

      $U\left(C\right)=C+k$

for some (not necessarily positive) constant $k$. If $k$ is positive, the people at the lab consider life without AI better than being wiped out in an AI-induced existential catastrophe. If $k$ is negative, they consider it worse.

Positing that the lab’s expected utility given survival is linear in capabilities, at least up to some threshold, is not a restriction on the model because we can stipulate that what “+1 unit of capabilities” means is simply “an increase in capabilities large enough to generate +1 util for the lab”. The assumption that $U$ increases unboundedly in $C$ is a more serious restriction, and relaxing it is discussed below.

Probability of survival

We will say that the probability of survival $P(C,S)$
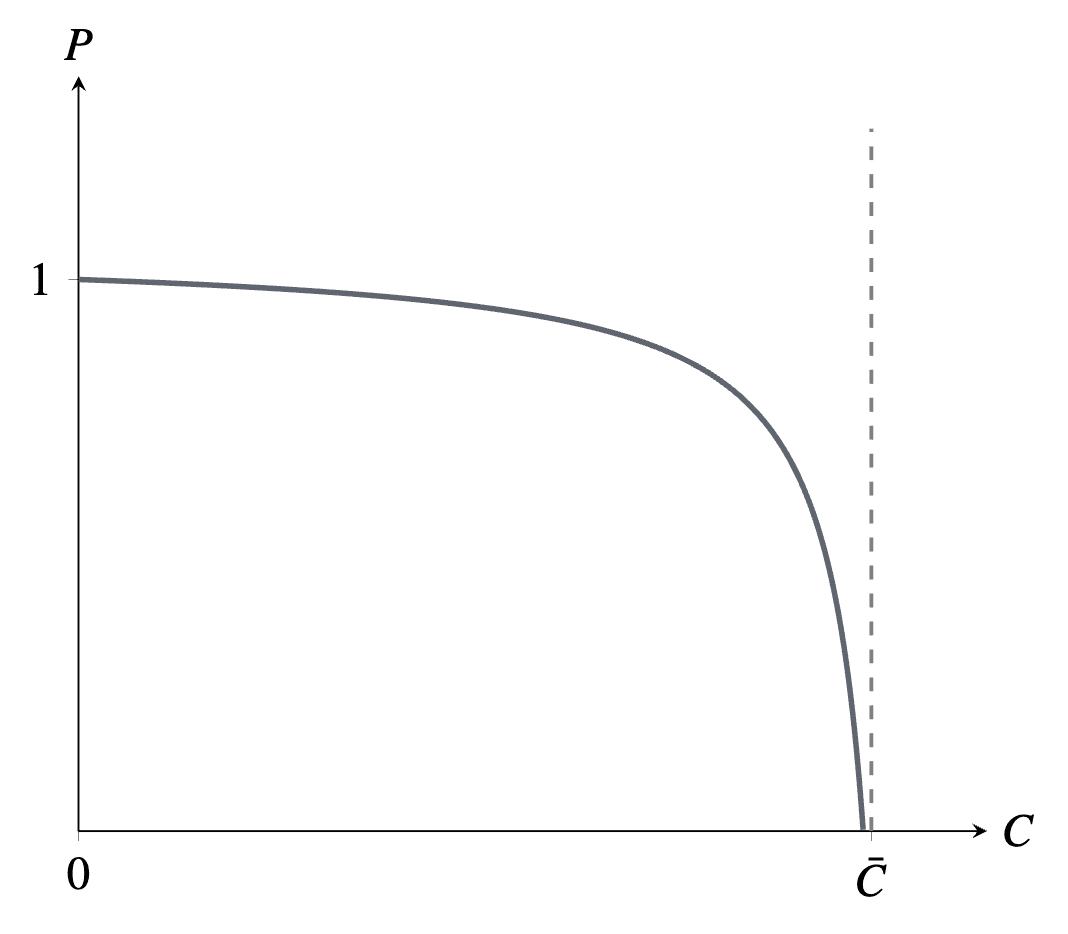
b1. equals 1 when $C=0$,
b2. decreases continuously in $C$,^[4] and
b3. increases in $S$ given $C>0$.

In this section and most of the next two, I’ll assume that $P(\cdot )$ is a particular function satisfying these conditions:

      $P(C,S)=e^{-\frac{C}{S}}$.

Unlike $U(\cdot )$, this choice of $P(\cdot )$ is a considerable loss of generality beyond the listed assumptions. A section below considers the extent to which the survival function can be changed before the results significantly change.

Summary

In sum, at least until the “changing the assumptions” section,

      ${\text{EU}}_{\text{lab}}=e^{-\frac{C}{S}}(C+k)$.

Of course nothing about a function of this shape has anything to do with existential catastrophe in particular. A utility function of this form could just as well capture the preferences of anyone deploying anything with some probability $P$ of one outcome whose utility is fixed, with $P$ increasing in “$C$”, and probability $1–P$ of a different outcome whose utility increases in “$C$”. $k$ then represents the size of the utility-gap between “good outcome but $C=0$” and “bad outcome”. We’ll keep referring to survival and so on mainly just to have a concrete case in mind.

Defining the game

If doing safety work (increasing $S$) does not change $C$, the probability of survival increases when more safety work is done. This is what happens in a two-stage game in which

1. The lab chooses a baseline level of safety work $\underset{–}{S}$ ($\ge 0$) and a degree of capabilities $C$ ($\ge 0$).
2. People outside the lab do $s$ ($\ge 0$) units of safety work. These top up the baseline, so $S=\underset{–}{S}+s$.

In this game, whatever the lab’s policy, higher $s$ straightforwardly results in higher $S$, and so higher probability of survival $e^{-\frac{C}{S}}$. There is no room for risk compensation.

But in reality the world is a messy dynamic game. People choose what to do with their time in light of what work others have already done, after some lag; others respond likewise; and so on. The “others choose, then you choose” model illustrated above, on which people often seem to intuitively operate,^[5] must have some truth to it: if you go into some career, others typically won’t adjust their behavior instantaneously. But so does the “you choose, then others choose” model at the other end of the spectrum, as might be illustrated here by a two-stage game in which

1. People outside the lab do $\underset{–}{S}$ units of safety work.
2. The lab chooses $C$. It also puts $s$ units of effort into safety, so $S=\underset{–}{S}+s$.

This is the sort of model that most fully allows for risk compensation. Here, higher $\underset{–}{S}$ may induce the lab to choose lower $s$ and/or higher $C$, so the effect of increasing $s$ on $e^{-\frac{C}{S}}$ is unclear.

Indeed, it would be more standard to refer to the phenomenon of higher $s$ inducing lower $S$ as crowding out of safety work, which is not the subject of this post, and to reserve the term risk compensation for the phenomenon of higher $s$ inducing higher $C$. To focus on risk compensation in this sense, therefore, we will spend the rest of the post considering the even simpler game in which

1. People outside the lab choose $S>0$.
2. The lab chooses $C\ge 0.$

Relative to the second game, this third game removes one of the two channels through which safety work done outside the lab can fail to increase $P$: since the lab is not bothering (or is not able) to do any safety work at all, there is no way for safety work done outside the lab to decrease the amount done by the lab. Nevertheless, as illustrated below, even the risk compensation effect in isolation (higher $S$ inducing higher $C$) can be extreme.

Result & explanations  

Result: the effect of safety work on probability of survival

To find the lab’s optimal choice of $C$ given $S$, i.e. how far it wants to push capabilities without over-doing the risk of an accident, take the derivative of its expected utility $e^{-\frac{C}{S}}(C+k)$ with respect to $C$ and set it to zero:

      $-\frac{1}{S}{e}^{-\frac{C}{S}}(C+k)+e^{-\frac{C}{S}}=0$

               $⟹-\frac{C+k}{S}+1=0$

                                $⟹C=S-k$.

(If $k>0$ and $S<k$, the lab’s optimal choice under the $C\ge 0$ constraint is to set $C=0$.)

If $k=0$—if the people at the lab consider life without AI to be as bad an outcome as an AI-induced existential catastrophe—then the probability of survival here equals $e^{-1}$, which is independent of S. The safety benefits of doing more safety work S are fully offset by inducing the lab to choose higher $C$. $S$ has no effect on the probability of survival.

If $k>0$—the (presumably more typical) case that people at the lab consider life without AI to be a better outcome than an AI-induced existential catastrophe—then probability of survival here equals 1 if $S\le k$ (because then $C=0$), and $e^{-(1-\frac{k}{S})}$ if $S>k$, which decreases in S. Safety work backfires.

Only if $k<0$, with AI-less life considered worse than death, does the probability of survival $e^{-(1-\frac{k}{S})}$ increase in S.

Alternative explanation

The lab sets $C$ so that

a) the proportional increase to $U$ from marginally increasing $C$, i.e. $1/(C+k)$, equals

b) the proportional decrease to $P$ from marginally increasing $C$.

(b) is constant, across values of $C$, for any given $S$. But $S$ is inversely proportional to (b).
So: suppose $S$ is doubled, so (b) halves. Then the lab wants to halve (a). So:

• When $k=0$, it has to more than double $C$ to halve $1/(C+k)$. With $S$ doubled but $C$ more than doubled, $C/S$ rises, and $P$ falls.
• When $k>$ ($<$) $0$, it has to more (less) than double $C$ to halve $1/(C+k)$. With $S$ doubled but $C$ more (less) than doubled, $C/S$ rises (falls), and $P$ falls (rises).

Let’s dwell a bit more on the intuition for the $k>0$ case, since it’s arguably both the most plausible and the most counterintuitive.

Suppose $k>0$, so that life is worth living even at $C=0$. If S is too low, the lab doesn't want to set $C>0$ at all. E.g. if $S=0.01$, even setting just $C=0.1=10S$ brings near-certain death ($P=e^{-10}$) for little benefit. But if $S$ is high enough—more than $k$—then setting $C>0$ becomes worthwhile, and $P$ falls from 1.

Once we recognize that increasing $S$ can induce a shift from $C=0$ to $C>0$, it is clear that safety increases have historically increased the incidence of accidents in all sorts of domains. I think it’s safe to say that if airplanes still crashed as frequently as the Wright brothers’ first prototypes, no one would use them (life without flight is still better than death), and the number of airplane crashes would therefore be even lower than it is.

The importance of the unbounded C assumption

Incidentally, in the case of airplanes, after they became safe enough to be widely used, further safety work greatly lowered the probability of a crash per flight. So in this context, the relationship between safety work and probability of survival is evidently U-shaped.

It makes sense that safety work would eventually not be offset much in the airplane context because here, recalling that $C$ is denominated in units of utility given survival, $C$ cannot be set arbitrarily high. Even if a plane were flown as fast and recklessly as would be optimal if safety were not a concern at all, this would not offer passengers infinite utility: other than a slightly cheaper ticket, and saving a few minutes on the safety video at the beginning, I’m not sure it would offer much utility at all.

As noted in the previous section, the assumption that $C$ can be set arbitrarily high is a strong one, producing simpler but more extreme risk compensation effects than follow when $C$ is bounded. Given bounded $C$ (and $k>0$), I expect that the U-shaped relationship between safety work and probability of survival is typical, and that the results we came to under the assumption that $C$ is unbounded roughly hold only when $C$ is far from its bound. This is discussed in the section below on bounded utility.

Economic intuition

There is also a more thoroughly “economic” intuition about the main result so far that I find helpful. I think it’s especially helpful for thinking about what changes when the survival function is different or $C$ is bounded, so this is put off to the next section.

Carrots and potatoes

Consider a consumer with preferences over two goods: carrots $C$ and potatoes $P$. She has a budget constraint, and a favorite basket subject to the budget constraint:

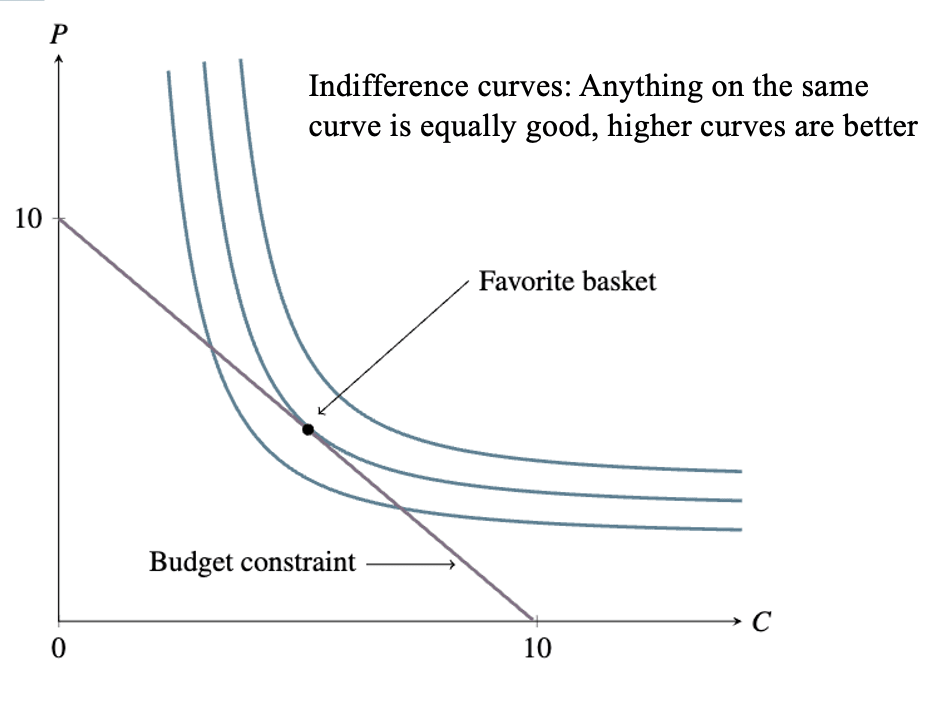
At first, say, the prices of the vegetables are equal. It takes as much land, water, farmer effort, etc. to grow one as to grow the other.

Now suppose the government wants people to eat more carrots, so it funds an improvement to carrot-farming technology. Once this improvement is developed, 1.2 carrots can be developed using the land (etc.) which it used to take to grow 1 carrot, and which it still takes to grow 1 potato. Assuming that the markets are competitive, carrots will now accordingly be cheaper than potatoes, and the consumer’s budget constraint will change. She will probably not want to buy fewer carrots than before, but the number of potatoes she wants to buy might well be more than, less than, or the same as before:

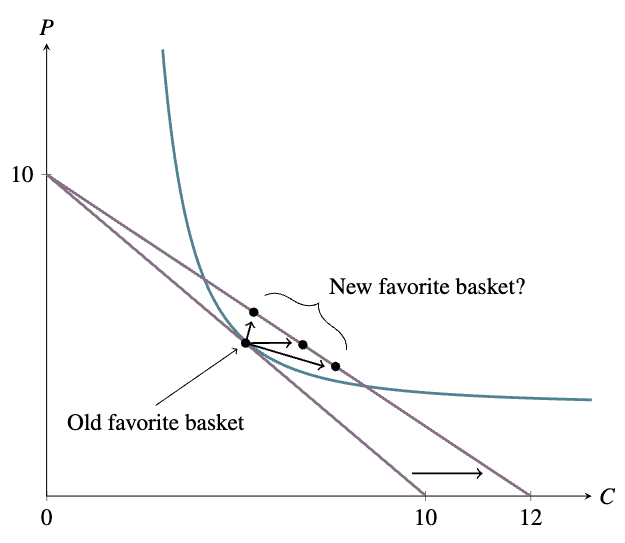
If she sees carrots and potatoes as very substitutable, such that a thought along the lines of “carrots and potatoes are basically the same, and carrots are cheaper now” predominates, the number of potatoes she buys will fall. If she sees the two vegetables as very complementary, such that a thought along the lines of “I like my stew to have a certain ratio of carrot to potato, so to some extent I’ll use the money I’m saving now that carrots are cheaper to buy more potatoes as well” predominates, the number of potatoes she buys will rise.

For an example of perfect substitutability, suppose the consumer’s utility function is

      $U(C,P)=C+kP$

for some $k>0$. This describes, for example, the case in which the consumer just cares about how many calories she gets and a potato has $k$ times as many calories as a carrot. In this case, letting ${\pi }_C$ and ${\pi }_P$ denote the prices of carrots and potatoes respectively, if ${\pi }_P<k{\pi }_C$ she only buys potatoes; if ${\pi }_P>k{\pi }_C$ she only buys carrots; and if ${\pi }_P=k{\pi }_C$ she doesn’t care how she splits her budget. Starting from the case in which ${\pi }_P=k{\pi }_C$ and she buys some of each, if ${\pi }_C$ falls at all, her potato demand plummets (she switches to only buying carrots), and if ${\pi }_C$ rises at all, her potato demand jumps (she switches to only buying potatoes).

There is a central case, in which the consumer’s demand for one good (potatoes) doesn’t depend on the price of the other (carrots). This is the case in which the consumer’s utility function is “Cobb-Douglas”. Without getting into Cobb-Douglas utility in general, the special case of Cobb-Douglas utility that will be relevant here is

      $u(C,P)=PC$.

Why doesn’t our consumer’s demand for one good depend on the price of the other here?

1. Whatever the prices are, she will always want to buy a positive amount of each good. If she buys zero of either, her utility is zero; if she buys a positive amount of both, her utility is positive.
2. Given that she is buying a positive amount of each good, her basket is optimal only if the extra utility she gets by spending a bit more on carrots equals the extra utility she gets by spending a bit more on potatoes:
                                                                          $\frac{P}{{\pi }_C}=\frac{C}{{\pi }_P}$.
   Otherwise she can increase her utility by spending a bit less on one and a bit more on the other. (The extra utility you get by spending a bit more on carrots equals the extra utility you get by getting a bit more carrot, $dU/dC=P$, times the number of carrots you get by spending a bit more on carrot, which is $1/{\pi }_C$. Likewise for potatoes.)
3. To maintain the equality above, whenever the price of carrots is multiplied by $m$, the number of carrots bought has to be multiplied by $1/m$.^[6]

Safety work as carrot-farming technology

In the model of the previous section, instead of defining the lab’s utility as a function of capabilities $C$ and safety effort $S$, we can define it as a function of capabilities $C$ and probability of survival $P$:

      ${\text{EU}}_{\text{lab}}=P(C+k)$.

The lab, like the consumer, faces a tradeoff between $C$ and $P$. This tradeoff depends on $S$:

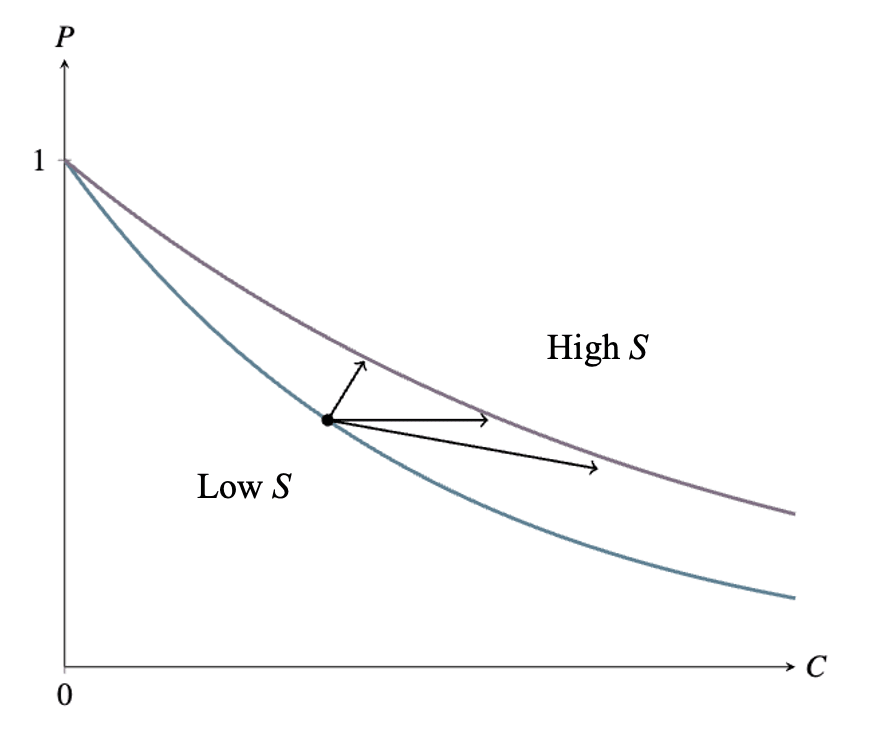
On the original framing, the variable the lab directly chooses is $C$, and this in turn yields some level of $P$ as a side effect. On the new framing, the lab, like a consumer, directly chooses $C$ and $P$ subject to a constraint. It is hopefully clear that the two framings are equivalent. One could just as well describe a consumer as directly choosing a number of carrots to buy, and winding up with some number of potatoes (the number affordable with all the money not spent on carrots) as a side effect.

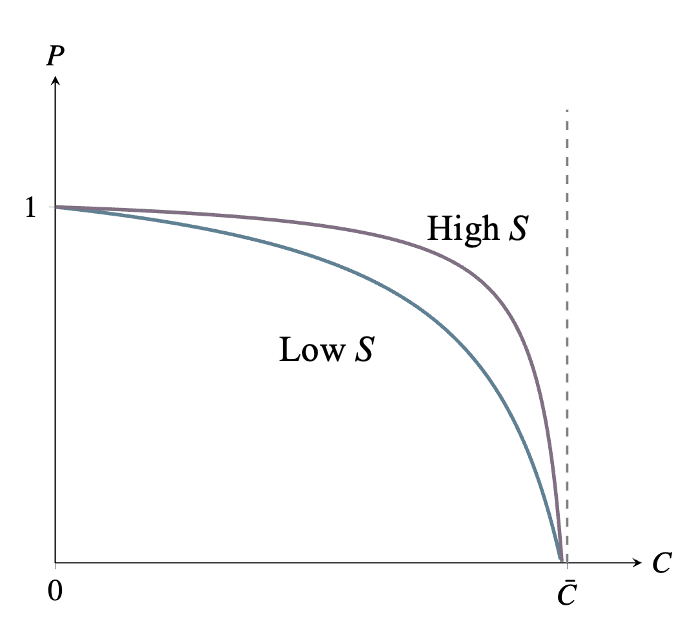
But the new framing makes it clearer that increases in safety work are effectively decreases to the “price” of $C$, at least under the survival function $P=e^{-\frac{C}{S}}$. Here, when $S$ is multiplied by $m$, the lab can multiply $C$ by $m$ while keeping $P$ fixed (“buying the same number of potatoes”). On the graph above, whatever the starting levels of $C$ and $P$, a given increase to $S$ shifts the level of $C$ affordable at each level of $P$ to the right by the same proportion. Though S stands for Safety, we shouldn’t be misled by the label: it’s precisely what we identified above as carrot-farming technology. It’s the thing a government should fund if it wants people to have more $C$, not more $P$.

When $k=0$, the lab’s preferences over $C$ and $P$ are Cobb-Douglas: $U(C,P)=PC$. It therefore responds to a cut in the price of $C$ (i.e. an increase to $S$) by increasing $C$ and keeping $P$ fixed, as we have seen.

When $k\ne 0$, the lab’s preferences are $u(C,P)=P(C+k)=PC+kP$. When $k>0$, this case is, as it looks, somewhere between the Cobb-Douglas and perfect-substitutability cases. The lab therefore responds to a cut in the price of $C$ by increasing $C$ to the point of lowering $P$, as we have also seen.

Generalizing the model

Probability of survival

Other survival functions

We have seen that, under the survival function $P=e^{-\frac{C}{S}}$, increases to S amount to “decreases in the price of $C$.” Increases to $S$ do not amount to decreases in the price of $C$ under all survival functions $P(C,S)$ satisfying b1-b3.

This relationship does hold well beyond the $P=e^{-\frac{C}{S}}$ case, however. That particular survival function was chosen for simplicity when differentiating with respect to $C$, but given b2 and b3, the “↑$S$ ≡ ↓${\pi }_C$” relationship holds whenever $P(C,S)$ satisfies
(*) there is a function $m(S,S^{\prime })$ such that, for all $S$, $S^{\prime }$, and $C$, $P(C,S)=P\left(m\right(S,S^{\prime })C,S^{\prime })$.

The interpretation is hopefully clear: (*) is precisely the condition under which moving from $S$ to $S^{\prime }$ is the same as dividing the price of $C$ by $m$, because whatever the original levels of $C$ and $P$, if the lab goes for $m$ times more $C$ after the $S$-change, it gets the original $P$. For example, survival function

      $P(C,S)=\frac{S}{C+S}$

also satisfies (*) (and indeed also with $m(S,S^{\prime })=S^{\prime }/S$), so all our results also hold with this survival function.

Furthermore, there is a sense in which, for any survival function $P(C,S)$ satisfying b1 and b3, $S$-increases have to look more like decreases to the price of $C$ than like decreases to the price of $P$, “on average”. When $S$ rises, the new curve lies above the old curve at all $C>0$ (by b3)—but not at $C=0$, because $P(0,S)=1$ for any $S$ (by b1). The amount by which the new curve lies above the old curve must therefore rise on average as $C$ rises from 0 to any positive number (though it does not necessarily rise monotonically).

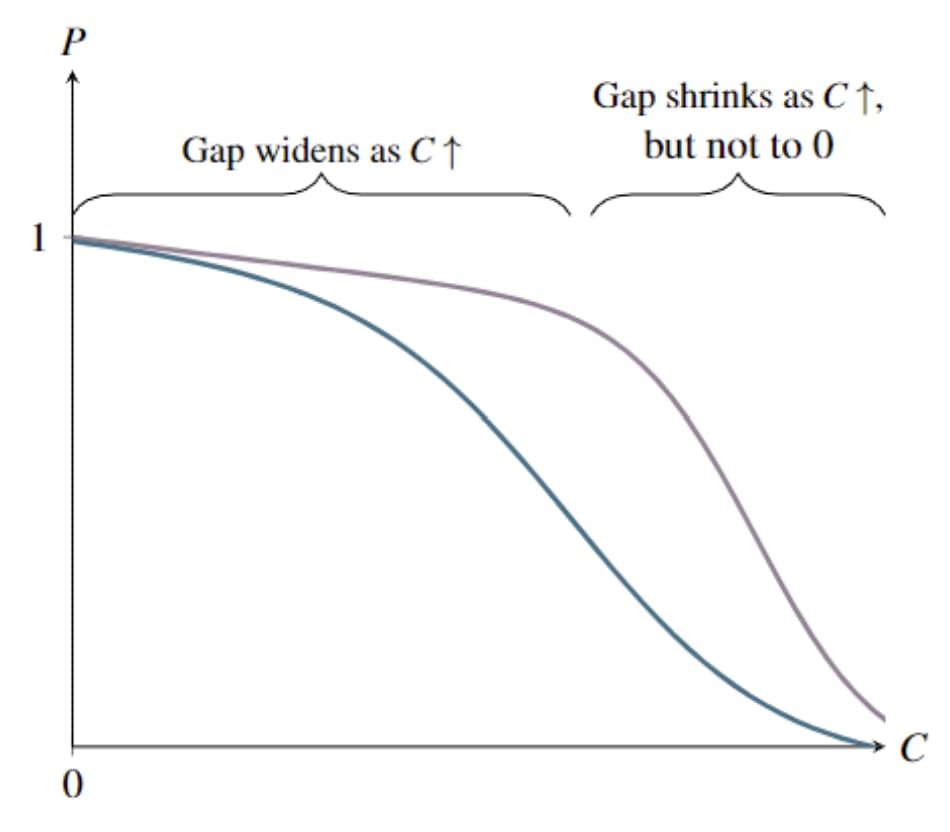
Given a “decrease to the price of potatoes”, the number of extra potatoes you can buy is higher the fewer carrots you buy. Here, that cannot happen. However few carrots you buy, you get at most one potato.

Misperceptions

So far, we have assumed that the lab knows what the survival function is. But a lab might be misperceiving it. Of course, many who work on AI safety believe that the big labs are currently generating greater risks than they are aware of.

This is not a reason to dismiss the logic of risk compensation, since while misperception can shrink the size of the effect, it can also exacerbate it or have no effect on it. Indeed, when Googling for existing materials on risk compensation, many of the top results introduce it with something like “people’s perception of risk decreases, and so people may feel that they can now afford to make riskier decisions” (from here). At least to my reading, wording like this suggests that one of the main concerns people have around risk compensation is that safety work can raise risk because people think the work is more effective than it is.

Given survival function $P(C,S)=e^{-\frac{C}{S}}$, a misperception never affects the sign of the effect of safety work on the probability of survival iff the perceived survival function $\tilde{P}(\cdot )$ also satisfies (*) with $m(S,S^{\prime })=S^{\prime }/S$.^[7] For example, suppose that $\tilde{P}(C,S)=e^{-\frac{C}{2S}}$: i.e. that the lab always thinks things are as safe as if twice as much safety work has been done than actually has been done. Then it sets $C=2S–k$. So again, an increase to $S$ induces a decrease to $C/S$ (so, an increase to the actual probability of survival) iff $k<0$, and so on.

Likewise, given survival function $P(C,S)=e^{-\frac{C}{S}}$ and perceived survival function $\tilde{P}(\cdot )$ satisfying (*) with $\tilde{m}(\cdot )$, the misperception magnifies the risk compensation induced by a move from $S$ to $S^{\prime }>S$ iff $\tilde{m}(S,S^{\prime })>m(S,S^{\prime })$, and lessens it iff the inequality is reversed. For example, if $\tilde{P}(C,S)=e^{-\frac{C}{S^z}}(z>0)$, then $\tilde{P}(\cdot )$ satisfies (*) with $\tilde{m}(S,S^{\prime })=(S^{\prime }/S{)}^z$. Given $S^{\prime }>S$, therefore, we have $\tilde{m}(S,S^{\prime })>m(S,S^{\prime })$ and so magnified risk compensation if $z>1$, and $\tilde{m}(S,S^{\prime })<m(S,S^{\prime })$ and so lessened risk compensation if $z<1$.

Utility given survival

Bounded utility

So far, our only significant assumption on utility given survival $U(\cdot )$ has been that $U$ increases unboundedly in $C$. Put another way, since $C$ is denominated in units of utility, we have assumed that there is no upper bound on achievable utility given survival.

But this assumption is unrealistic, especially once we note that increases to $C$ can lower the lab’s utility given survival simply by being expensive. Presumably, at any given time, higher choices of $C$ come with higher profits but also higher costs, so that even in the event that safety is no concern—even if $P(C,S)=1$ for all $C$, $S$—$U$ is maximized at some finite level by some finite amount of capabilities and deployment.^[8]

The simplest way to impose this restriction is to modify the game so that, in “stage 2”, the lab chooses $C\in [0,\overline{C}]$ for some finite $\overline{C}$, rather than any $C\ge 0$. Under this modification, the lab’s optimal choice of $C$ is not {$0$ if $S\le k$; $S-k$ otherwise} but {$0$ if $S\le k$; $\overline{C}$ if $S\ge \overline{C}+k$; $S-k$ otherwise}. Increases to $S$ then have the effects we have seen up to the point that $S=\overline{C}+k$, past which further increases to $S$ have no impact on $C$ and raise $P$ in the intuitive way.

This observation is enough to capture the important point: if capabilities are running up against an upper bound, then safety work cannot be offset. But the framework above has a somewhat suspicious discontinuity. For any value of $k$, an increase to $S$ induces a one-for-one increase to $C$ until $S=\overline{C}+k$, past which increasing $S$ does not affect $C$ at all. A more reasonable-seeming result, at least to my mind, would have been one in which, however high $S$ is, the induced choice of $C$ is still constrained at least a little bit by safety. Making planes 1% safer wouldn’t increase pilot carelessness (or miles flown) by 1%, but come on, at least in expectation it would increase these a little.

The reason for the implausible discontinuity can be seen if we describe utility given survival as a function $u(\cdot )$ of some more conventional measure of capabilities—say, denoted $c$, so that utility given survival is $u\left(c\right)$ with $u\left(0\right)=k$. If $u(\cdot )$ is differentiable, then if it is maximized at some $c^{\ast }>0$—i.e. if $u\left(c^{\ast }\right)=\overline{C}+k$—we must have $u^{\prime }\left(c^{\ast }\right)=0$. In other words, increases to capabilities-as-conventionally-understood c have almost no impact on $U$ around $c^{\ast }$. It then follows that a unit of increase to $C$ must, around its maximum value of $\overline{C}$, consist of a huge increase to capabilities-as-conventionally-understood, and thus, presumably, a huge decrease to $P$. The chosen level of $C$ thus remains at least slightly below its maximum, and there is always at least a little bit of room for safety work to induce an increase to it.

After this modification, the survival function $P(C,S)$ cannot globally satisfy (*). It might approximately satisfy (*) for ranges of $S$, $S^{\prime }$, and $C$ with $P(C,S)=P(C^{\prime },S^{\prime })$ for $C,C^{\prime }\ll \overline{C}$—that is, safety work might act like a decrease to the relative price of capabilities when the chosen level of capabilities would be far from its upper bound both before and after the safety improvement. Indeed, by the argument of the section above on other survival functions, it is still the case that, over some range, increases to $S$ must produce greater increases to the probability of survival the higher the choice of $C$ and so act roughly like subsidies on $C$. But $P(C,S)$ probably doesn’t come close to satisfying (*) for levels of $C$ given $S$, $S^{\prime }$, $C$ with $P(C,S)=P(C^{\prime },S^{\prime })$ for $C\approx \overline{C}$ or $C^{\prime }\approx \overline{C}$. Instead, the gap between the graphs of $P(C,S)$ and $P(C,S^{\prime })$ probably widens as $C$ moves to the left. Around $\overline{C}$, safety work subsidizes potatoes after all.

Implications of bounded utility

To try a thought experiment: heroin is much less widely used than alcohol, despite apparently being more enjoyable, presumably because it is so much more dangerous.^[9] This implies that the utility currently being derived from heroin is a very small fraction of what it would be if heroin were only as harmful as alcohol, let alone what it would be if heroin were harmless: $C\ll \overline{C}$. Given the logic outlined above, this in turn predicts that it would not be surprising if risk compensation were more than complete in the heroin case, on the current margin. And indeed, when we compare heroin deaths to alcohol deaths, this conclusion seems reasonable. Heroin currently causes fewer deaths than alcohol, but if it were made precisely as safe as alcohol, it seems likely that it would (eventually) be more widely used than alcohol currently is, and would thus (eventually) cause more deaths than alcohol currently does.

Likewise, if indeed risk compensation is more extensive in NASCAR racing than in ordinary driving, and more extensive in driving than it currently is in flying, I expect “distance from the utility bound” is a large part of the explanation why. The feasible utility gains to driving or (especially) flying as recklessly as if safety were no concern are small: in these domains, $C$ is already near $\overline{C}$. In NASCAR, by contrast, it is often the case that driving just a little bit faster significantly increases a driver’s probability of victory. To the extent that safety concerns are constraining drivers’ choices of $C$ at all, therefore, they are often constraining them to levels significantly below $\overline{C}$, and something closer to the “unbounded $C$” logic applies.

Incidentally, the NASCAR observation brings us closer to an intuition for why risk compensation appears to generally be a more significant worry in “arms race” scenarios, as studied by Trager and the others cited in the introduction, than in the single-actor scenarios considered here. Beyond noting this, since those scenarios are more complicated, and since (as cited) there are already materials designed to build intuition around them, I won’t get into them here.

Even if one lab pulls far enough ahead in AI development that the relevant model is closer to a single-actor model than to an arms race model, however, the reasoning above suggests that risk compensation will eventually be a more significant factor than it currently is. Today, while even the most advanced AI systems are neither very capable nor very dangerous, safety concerns are not constraining $C$ much below $\overline{C}$. If technological advances unlock the ability to develop systems which offer utopia if their deployment is successful, but which pose large risks, then the developer’s choice of $C$ at any given $S$ is more likely to be far below $\overline{C}$, and the risk compensation induced by increasing $S$ is therefore more likely to be strong.

Takeaways

On how significant risk compensation is

It should sometimes be expected to be more than full

Anecdotally, there seems to be a widespread impression that, when people are being rational, risk compensation should, at worst, only partially nullify the effects of safety work. But as we’ve seen, it can go either way, depending on the details. If (a) life without deployment is better than suffering the catastrophe ($k>0$) and (b) the utility being achieved from current deployment is far from the level that would be achieved if safety were no concern ($C\ll \overline{C}$), then safety work should typically be expected to induce risk compensation that is more than complete. This suggests to me that risk compensation is a possibility worth taking very seriously.

But, probably, it is usually only partial

When measured, efforts to make systems safer usually seem to have some effect in the intuitive direction. This makes sense, for at least two reasons. First, conditions (a) and (b)—especially (b), I think—can fail to hold. Second, others typically respond to an increase in safety work only with a lag. Between when safety work has been done and when the capabilities and/or deployment have ramped up accordingly, accident probability is unambiguously lower.

Measurement

On the other hand, the lag makes it harder to know what effect a given bit of safety work has in the long run. The sense “I haven’t seen capabilities or deployment speed up because of my safety paper from last month” might be misleading. If there is work I don’t know about that attempts to estimate the degree of risk compensation in various existential-risk-relevant domains, then it will be great if someone comments about it! If not, it might be worth thinking about whether it could be estimated in some of these domains; and in the meantime, hopefully theory-informed guesses are better than nothing.

On what to do in light of it

I expect that people actually working on reducing risk (existential or otherwise) in some domain will have more precise ideas than I do about the practical implications of risk compensation. But here are at least a few broad conclusions that come to my own mind, if only to illustrate the idea. I assume throughout that your goal is just to maximize the “probability of survival”.

When doing safety work, seek weak-risk-compensation domains

All else equal, prefer to do safety work in domains…

1. In which there is a long lag between when the safety measure will be implemented and when it will be possible to compensate for it by implementing more capabilities in the relevant area.
2. That “lowers the price of $P$ rather than $C$”. That is, look for work that increases the probability of survival at lower levels of capabilities (as measured by utility given survival) by more, not less, than it increases the probability of survival at higher levels of capabilities. The ideal scenario is to make it much safer to deploy the medium-capability system that was going to be deployed anyway, without also making it much safer to deploy the high-capability system that wasn’t going to be deployed due to risk fears. (To reiterate, the claim is just that risk compensation pushes in this direction, all else equal. There are many other reasons to focus on making highest-capability systems safer in particular. For instance, if more work is already going into the medium-capability systems already on the verge of deployment than on the high-capability systems that will not be deployed for years, then work of the latter kind runs less risk of being nullified by crowding out of safety work.)
3. In which “$k$” is...
   1. lower, if the work is primarily “lowering the price of capabilities”. For instance, maybe the value of life without AI ($k$) is higher in the US than in China, since the US is the richer country. If so, then in the event that the US and China are working on very different kinds of AI systems, work that makes the American-style systems safer in a way where the benefits of the safety work increase the more advanced or widely deployed the systems are should be expected to induce more risk compensation than work on making the Chinese-style systems safer in such a way (again, all else equal). (If life without AI is better for the relevant decision-makers in China than in the US, this goes the other way.)
   2. higher, if the work is primarily “lowering the price of survival”. Again, recall that the higher $k$ is, the more substitutable $P$ and $C$ are, so slightly lowering the price of one of the two goods motivates a more significant shift toward that good.
4. In which “$\tilde{m}<m$”. That is, prefer work that is perceived to lower risk by less than it does. (An extreme case would be to raise $S$ secretly, if this is possible. But in practice, presumably, an insight about how to make an AI system safer doesn’t have any impact—and so doesn’t really constitute an increase to $S$—unless the lab is aware of it and implements it.)

Seek ways of increasing safety other than “safety work”

Naturally, if safety work seems likely to induce significant risk compensation, it may make sense to look for work that won’t. Not all work to lower the chance of a catastrophe consists of safety work in the sense defined here, i.e. work “actually making the thing safer”. For example, you might push for policy that raises $S$ and imposes a cap on $C$. Or, if you think that the risk associated with implementing a given $C$ is higher than the relevant decision-maker thinks it is, you might try to communicate this, e.g. via model evaluations (or “evals”). These approaches might backfire to some extent too, of course, but if so it will be for different reasons.

Thanks to Guive Assadi, Tom Davidson, Isabel Juniewicz, Fin Moorhouse, GovAI lunch-and-learn attendees (especially Jamie Bernardi), and many others who have given helpful comments on various iterations of this content. Thanks to Tom Houlden for making the graphs.

1. ^{^}

   The term “risk homeostasis” is also sometimes used, but typically reserved for the case in which risk compensation is enough to return risk precisely to its original level.

2. ^{^}

   Many studies in other domains (including some follow-ups to Peltzman) have found little or no risk compensation, and this leads some to conclude that the whole idea is just a theoretical possibility that turns out not to be real. I don’t think this is the right conclusion, for two reasons. First, there’s no way this conclusion holds in the extreme. To repeat one famous thought experiment, drivers would obviously drive more carefully if seat belts were banned and steering wheels had giant metal spikes pointing at the driver’s chest. Second, risk compensation can be difficult to observe for a few reasons. For example, it might be found that the number of car accidents doesn’t jump up (or, not much) once a safety measure is implemented. But it seems likely that even if a measure does eventually affect driver behavior, it does so only with a long lag, since it takes time for drivers to appreciate the fact that their cars have become safer (via, say, seeing fewer injured friends and relatives or repeatedly viewing commercials emphasizing the new features); for drivers to adjust their driving habits; and for substitutionary measures such as speed limits to adjust. This lag issue in particular is discussed a bit more in the “defining the game” section and the conclusion.

3. ^{^}

   Note that this is distinct from the possibility that RLHF itself allowed for the development of more advanced capabilities, discussed e.g. by Christiano (2023).

4. ^{^}

   That is, we will say that what we mean by setting $C=0$ is setting capabilities at the maximum level for which the probability of survival is 1. Note that, when this is the case, we can harmlessly impose the constraint that $C\ge 0$, since it will never be optimal for the lab to choose $C<0$.

5. ^{^}

   And which is an implicit premise of e.g. the “ITN” formula, at least as presented on the 80,000 Hours page about it.

6. ^{^}

   That is, as long as her budget stays fixed. If $C$ is multiplied by more [less] than $1/m$, $P$ must rise [fall] for the equality to be maintained. Since the price of potatoes has not changed, this would mean spending more [less] on both goods.

7. ^{^}

   Given that $S$ is high enough to motivate $C>0$ on both $P(\cdot )$ and $\tilde{P}$(·).

8. ^{^}

   Note that this is not a philosophical discussion about the plausibility of unbounded utility in principle, but a discussion about whether, given the technological possibilities available at a given time, it is possible to achieve any level of utility given survival by putting out AI that is sufficiently capable or widely deployed.

9. ^{^}

   And because it is illegal and socially discouraged, but of course this is also largely because it is so dangerous.