A huge thanks to @Agustín Covarrubias 🔸 for his feedback and support on the following article:
Shapley values are an extremely popular tool in both economics and explainable AI.
In this article, we use the concept of “synergy” to build intuition for why Shapley values are fair. There are four unique properties to Shapley values, and all of them can be justified visually. Let’s dive in!
The Game
On a sunny summer day, you and your two best friends decide to run a lemonade stand. Everyone contributes something special: Emma shares her family’s secret recipe, Liam finds premium-quality sugar, and you draw colorful posters.
The stand is a big hit! The group ends up making $280. But how best to split the profits? Each person contributed in a different way, and the success was clearly due to teamwork…
Luckily, Emma has a time machine. She goes back in time — redoing the day with different combinations of team members and recording the profits. This is how each simulation went:
| Who was involved? | Total profits |
|---|---|
| Only Emma | $20 |
| Only you | $30 |
| Only Liam | $10 |
| Emma and you | $90 |
| You and Liam | $100 |
| Liam and Emma | $30 |
| Emma, Liam, and you | $280 |
Individually, Emma makes 20 dollars running the lemonade stand, and you make 30 dollars. But working together, the team makes 90 dollars.
The sum of individual profits is 20 + 30 = 50 dollars, which is clearly less than 90 dollars. That extra 90 - 50 = 40 dollars can be attributed to team dynamics. In game theory, this bonus is called the “synergy” of you and Emma. Let’s visualize our scenario as a Venn diagram.
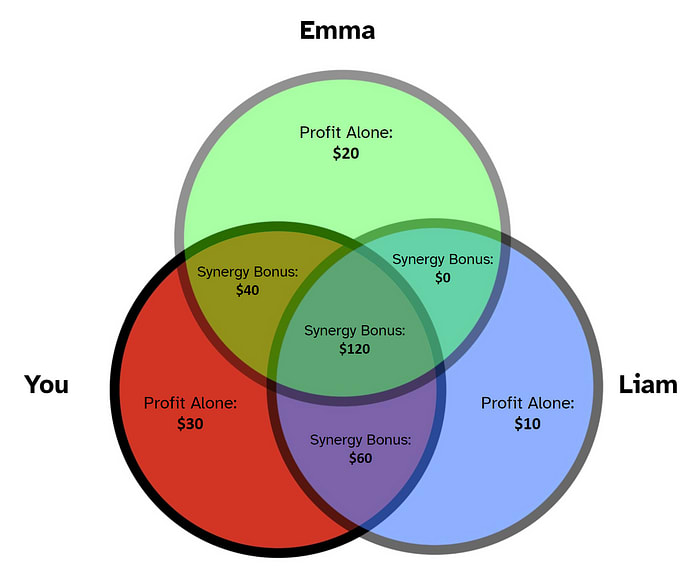
The synergy bonuses in the Venn diagram are “unlocked” when the intersecting people are part of the team. To calculate total profit, we add up all areas relevant to that team.
For example, when the team consists of just you and Liam, three portions of the Venn diagram are unlocked: the area exclusive to you (30 dollars), the area exclusive to Liam (10 dollars), and the area exclusively shared by you and Liam (60 dollars). Adding these areas together, the total profit for team “You and Liam” comes out to 30 + 10 + 60 = 100 dollars.
Referring to our Venn diagram, the same formula holds true for every other team:
| Team members | Sum of synergies | Total profits |
|---|---|---|
| Emma | $20 | $20 |
| You | $30 | $30 |
| Liam | $10 | $10 |
| Emma, You | $20 + $30 + $40 | $90 |
| You, Liam | $30 + $10 + $60 | $100 |
| Liam, Emma | $10 + $20 + $0 | $30 |
| Emma, You, Liam | $20 + $30 + $10 + $40 + $60 + $0 + $120 | $280 |
Emma and Liam are impatient and want their fair share of money. They turn to you, the quick-witted leader for help. While staring at the Venn diagram, an idea strikes!
Take a moment to look over the visual. How would you slice up the Venn diagram fairly? Pause here, and continue when ready.
You decide to take each “synergy bonus” and cut it evenly among those involved.
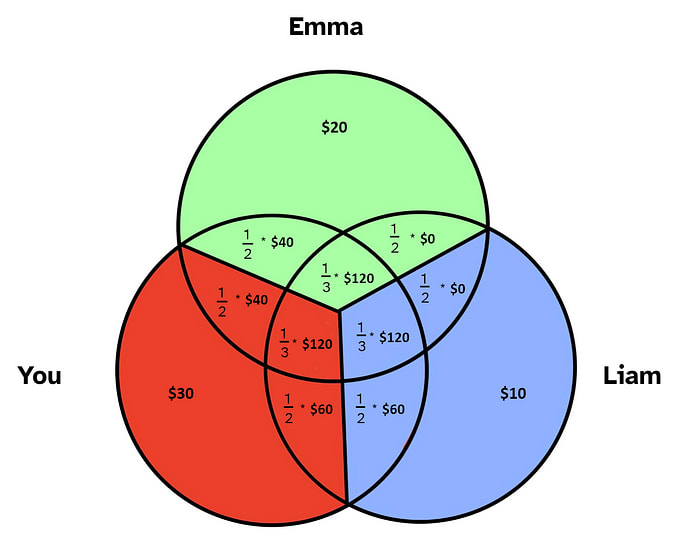
Doing the math, each person’s share comes out to:
Emma and Liam agree the splits are fair. The money is handed out, and everyone skips happily home to dinner.
In this story, the final payouts are the Shapley values of each team member. This intuition is all you need to understand Shapley values. For the adventurous reader, we now tie things back to formal game theory.
The Formalities
Shapley values are a concept from cooperative game theory. You, Liam, and Emma are all considered “players” in a “coalition game”. Every possible “coalition” (or team) has a certain “payoff” (or profit). The mapping between coalition and payoff (a.k.a. which just corresponds to our first table of profits) is called the “characteristic function” (as it defines the nature, or *character*, of the game).
We define a set of players (which, in this case, is You, Emma, and Liam), and a characteristic function , where :
We can see how this is the same mapping we had in our table of profits by players:
| Who was involved? | Total profits |
|---|---|
| Only Emma | $20 |
| Only you | $30 |
| Only Liam | $10 |
| Emma and you | $90 |
| You and Liam | $100 |
| Liam and Emma | $30 |
| Emma, Liam, and you | $280 |
We also define a synergy function labeled where :
Similarly, the synergy function just corresponds to areas of the Venn diagram:
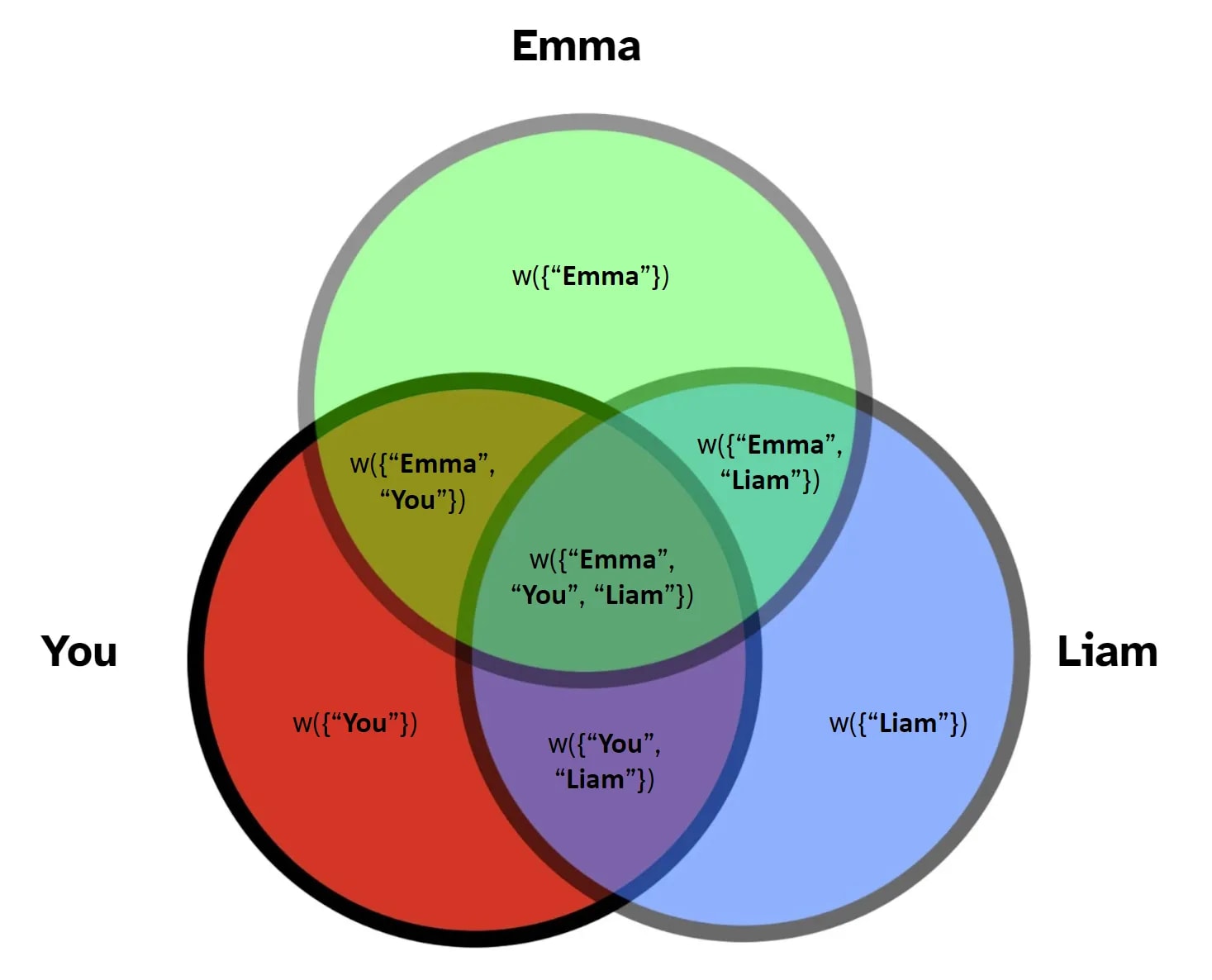
Thus, for a given player , the Shapley value is written as:
Which, in more compact notation, becomes:
The last is exactly the formula described on Wikipedia.
Concluding Notes
Shapley values are the ONLY way to guarantee:
- Efficiency — The sum of Shapley values adds up to the total payoff for the full group (in our case, $280).
- Symmetry — If two players interact identically with the rest of the group, their Shapley values are equal.
- Linearity — If the group runs a lemonade stand on two different days (with different team dynamics on each day), a player’s Shapley value is the sum of their payouts from each day.
- Null player — If a player contributes nothing on their own and never affects group dynamics, their Shapley value is 0.
Take a moment to justify these properties visually.
No matter what game you play and who you play with, Shapley values always preserve these natural properties of “fairness”.
Hopefully, you have gained some intuition for why Shapley values are “fair” and why they account for interactions among players. Proofs and more rigorous definitions can be found on Wikipedia.
Thanks for reading! :)

Thanks for posting this.
Do we have an intuition for how to apply shapely values in typical EA scenarios, for example: • How much credit goes to donors, vs charity evaluators, vs object level charities? • How much credit goes to charity founders/executives, vs other employees/contractors? • How much credit goes to meta vs object organizations?
Seconding this question, and wanted to ask more broadly:
A big component/assumption of the example given is that we can "re-run" simulations of the world in which different combinations of actors were present to contribute, but this seems hard in practice. Do you know of any examples where Shapley values have been used in the "real world" and how they've tackled this question of how to evaluate counterfactual worlds?
(Also, great post! I've been meaning to learn about Shapley values for a while, and this intuitive example has proven very helpful!)
Thanks for cross posting, this got Shapley values to "click" for me!
Executive summary: Shapley values, which determine fair allocation of rewards in cooperative games, can be intuitively understood using Venn diagrams to visualize how individual contributions and synergies between players combine to create total value.
Key points:
This comment was auto-generated by the EA Forum Team. Feel free to point out issues with this summary by replying to the comment, and contact us if you have feedback.