Thanks for sharing, Nicholas. For reference:

• Veganuary started in the United Kingdom (UK) in 2014, and I estimate the production of broilers per person in the UK in January increased 4.27 times as fast from 2014 to 2024 as from 1994 to 2013. Note data about consumption (production plus net imports) would be more informative.
• According to YouGov's polls, the fraction of vegans (2 %), pescetarians (3 %), vegetarians (5 %), flexitarians (13 %), and meat eaters (73 %) in the UK was the same in mid 2019 and the start of 2024.

Tell me if I'm understanding this correctly:

1. My (rough) numbers suggest a 6% chance that 100% of people die
2. According to a fitted power law, that implies a 239% chance that 10% of people die

On 1, yes, and over the next 10 years or so (20 % chance of superintelligent AI over the next 10 years, times 30 % chance of extinction quickly after superintelligent AI)? On 2, yes, for a power law with a tail index of 1.60, which is the mean tail index of the power laws fitted to battle deaths per war here.

I think it's very unlikely that an AI catastrophe kills 10% of the population in the next 10 years (not 10^-6 unlikely, more like 10^-3 unlikely).

I meant to ask about the probability of human population becoming less than (not around) 90 % as large as now over the next 10 years, which has to be higher than the probability of human extinction. Since 10^-3 << 6 %, I guess your probability of a population loss of 10 % or more is just slighly higher than your probability of human extinction.

Even if you put 99% credence in this model, surely P(extinction) will be dominated by other models? Even within the model, P(extinction) should be higher than that based on uncertainty about the value of the alpha parameter.

I think using a power law will tend to overestimate the probability of human extinction, as my sense is that tail distributions usually starts to decay faster as severity increases. This is the case for the annual conflict deaths as a fraction of the global population, and arguably annual epidemic/pandemic deaths as a fraction of the global population. The reason is that the tail distribution has to reach 0 for a 100 % population loss, whereas a power law will predict that going from 8 billion to 16 billion deaths is as likely as going from 4 billion to 8 billion deaths.

Thanks, Michael. I think your numbers suggest your unconditional probability of human extinction over the next 10 years is 6 % (= 0.3*0.2). Power laws fit to battle deaths per war have a mean tail index of 1.60, such that battle deaths have a probability of 2.51 % (= 0.1^1.60) of becoming 10 times as large. Applying this to your estimate would suggest a probability of a 10 % population drop over the next 10 years of 2.39 (= 0.06/0.0251), i.e. impossibly high. What is your guess for an AI catastrophe killing 10 % of the population in the next 10 years? I suspect it is not that different from your guess for the probability of extinction, whereas this should be much lower according to typical power laws describing catastrophe deaths?

For reference, I think the probability of human extinction over the next 10 years is lower than 10^-6. Somewhat relatedly, fitting a power law to Metaculus' community predictions about small AI catastrophes, I estimated a probability of human extinction before 2100 due to an AI malfunction of 0.004 %. 

Just for context:

• Compensation: The baseline compensation for this role is $453,068.02, which would be distributed as a base salary of $430,068.02 and an unconditional 401(k) grant of $23,000 for U.S. hires.
  • This assumes a location in the San Francisco Bay Area; compensation would be lower for candidates based in other locations. 

Thanks for sharing, Steve.

We’d like to celebrate and showcase our organizations and connect people like you to impactful opportunities in our community, so we are hosting an online event on Thursday, 5 December, from 5 to 9:00 PM GMT.

Will all the opportunities also be shared publicly on AIM's job board? By the way, you are listing roles there whose deadline was like 2 weeks ago (November 3).

Thanks for sharing.

If you would like access to the full report, please complete this Google form.

I would be curious to know why you have decided to keep the full report private.

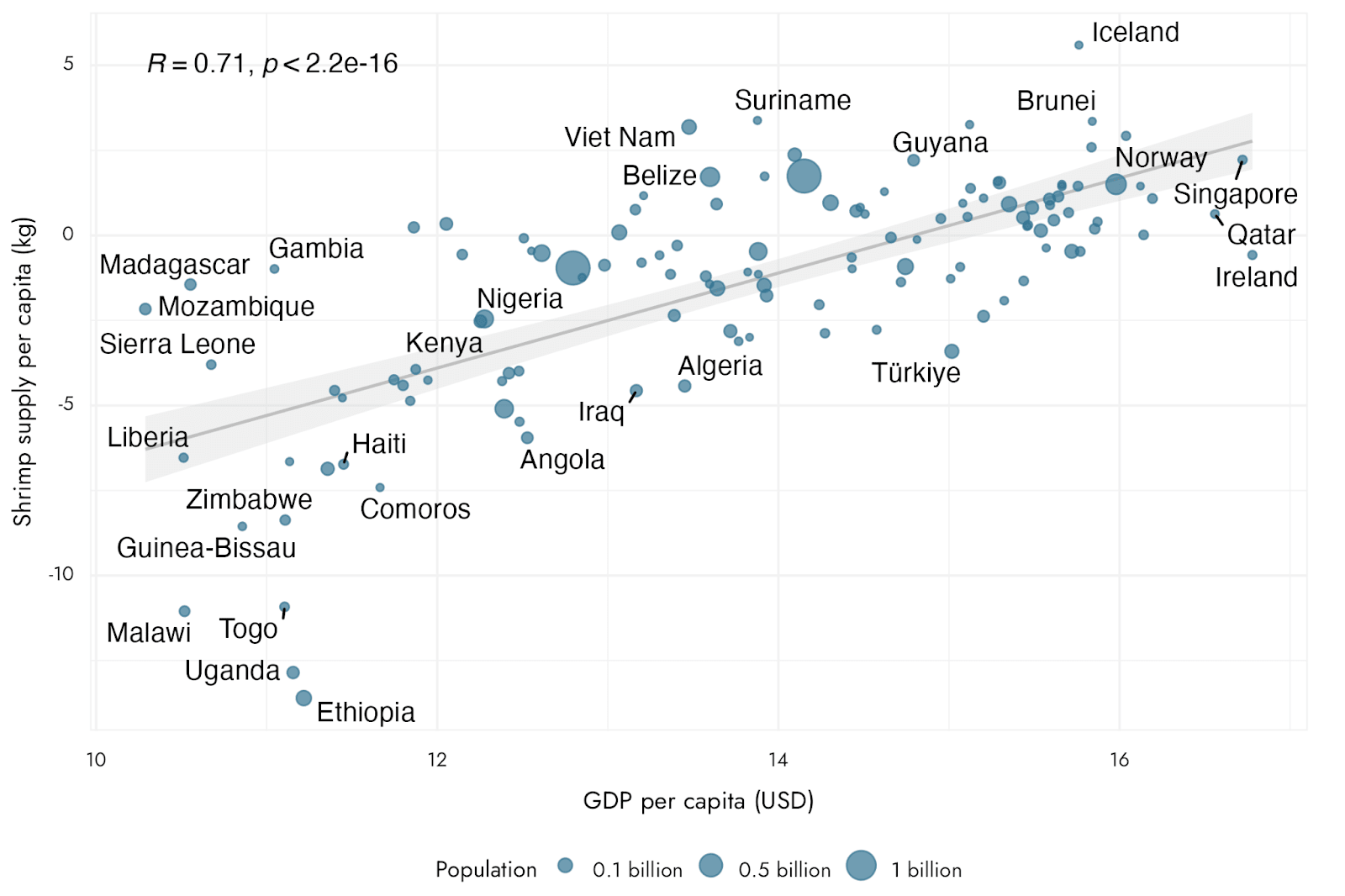
Nice graph! How can shrimp supply per capita be negative? Are you showing values relative to the mean across countries?

Hi Jeff.

But I'm not aware of any projects that aim to advise what we might call "Small Major Donors": people giving away perhaps $20k-$100k annually.

How about Ambitious Impact's funding circles, which have a minimum contribution "typically ranging from $10,000 to $100,000" (per year?)?

Hi Toby and Will. Not sure if it is intended, but the running total of votes does not seem to be available.

Thanks for sharing, Daniela. Have you considered researching ways of increasing funding to effective animal welfare interventions?

Thanks for sharing, Elisa. This is listed on Animal Advocacy Careers' job board, but not on 80 k's job board, so I have just let them know about it.