(Note: I privately submitted this essay to the red-teaming contest before the deadline passed, now cross-posting here. Also, this is my first ever post, so please be nice.)
Summary
- Longtermists believe that future people matter, there could be a lot of them, and they are disenfranchised. They argue a life in the distant future has the same moral worth as somebody alive today. This implies that analyses which discount the future unjustifiably overlook the welfare of potentially hundreds of billions of future people, if not many more.
- Given the relationship between longtermism and views about existential risk, it is often noted that future lives should in fact be discounted somewhat – not for time preference, but for the likelihood of existing (i.e., the discount rate equals the catastrophe rate).
- I argue that the long-term discount rate is both positive and inelastic, due to 1) the lingering nature of present threats, 2) our ongoing ability to generate threats, and 3) continuously lowering barriers to entry. This has 2 major implications.
- First, we can only address near-term existential risks. Applying a long-term discount rate in line with the long-term catastrophe rate, by my calculations, suggests the expected length of human existence is another 8,200 years (and another trillion people). This is significantly less than commonly cited estimates of our vast potential.
- Second, I argue that equally applying longtermist principles would consider the descendants of each individual, when lives are saved in the present. A non-zero discount rate allows us to calculate the expected number of a person’s descendants. I estimate 1 life saved today affects an additional 93 people over the course of humanity’s expected existence.
- Both claims imply that x-risk reduction is overweighted relative to interventions such as global health and poverty reduction (but I am NOT arguing x-risks are unimportant).
Discounting & longtermism
Will MacAskill summarised the longtermist ideology in 3 key points: future people matter (morally), there are (in expectation) vast numbers of future people, and future people are utterly disenfranchised[1].Future people are disenfranchised in the sense that they cannot voice opinion on matters which affect them greatly, but another way in which they are directly discriminated against is in the application of discount rates.
Discounting makes sense in economics, because inflation (or the opportunity to earn interest) can make money received earlier more valuable than money obtained later. This is called “time preference”, and it is a function of whatever discount rate is applied. While this makes sense for cashflows, human welfare is worth the same regardless of when it is expressed. Tyler Cowen and Derick Parfit[2] first argued this point, however, application of a “social” discount rate is widely accepted and applied (where the social discount rate is derived from the “social rate of time preference”)[3].
Discounting is particularly important for longtermism, because the discount factor applied each year accumulates over time (growing exponentially), which can lead to radical conclusions over very long horizons. For example, consider the welfare of 1 million people, alive 1500 years in the future. Applying a mere 1% discount rate implies the welfare of this entire population worth less than 1/3 of the value of a person alive today[4]. Lower discount rates only delay this distortion – Tarsney (2020) notes that in the long run, any positive discount rate “eventually wins”[5]. It is fair to say that people in the distant future are “utterly disenfranchised”.
Existential risk
Longtermism implies that we should optimize our present actions to maximize the chance that future generations flourish. In practice, this means reducing existential risk now, to maximize future generation’s probability of existing. (It also implies that doing so is a highly effective use of resources, due to the extremely vast nature the future.) Acknowledging existential risk also acknowledges the real possibility that future generations will never get the chance exist.
It's not surprising then, that it seems widely acknowledged in EA that future lives should be discounted somewhat – not for time preference, but accounting future people’s probability of actually existing[6]. What I do consider surprising, is that this is rarely put into practice. Projections of humanity’s potential vast future are abundant, thought similar visualizations of humanity’s “expected value” are far harder to find. If the discount rate is zero, the future of humanity is infinite. If the discount rate is anything else, our future may be vast, but it’s expected value is much less.
The Precipice
I believe the reason for this is the Precipice, by Toby Ord. I draw heavily on this book[7], and everything I’ve written above is addressed in it in some way or another. Ord suggests that we discount only with respect to the “catastrophe rate”, which is the aggregate of all natural and anthropogenic risks, and notes that the catastrophe rate must vary over time. (1 – the annual catastrophe rate is equal to humanity’s probability of surviving a given year.)
Living at “the precipice” means that we live in a unique time in history, where existential risk is unusually high, but if we can navigate the next century, or few centuries, then the rate will be reduced to zero. If true, this would justify a non-zero discount rate[8], but this is not realistic.
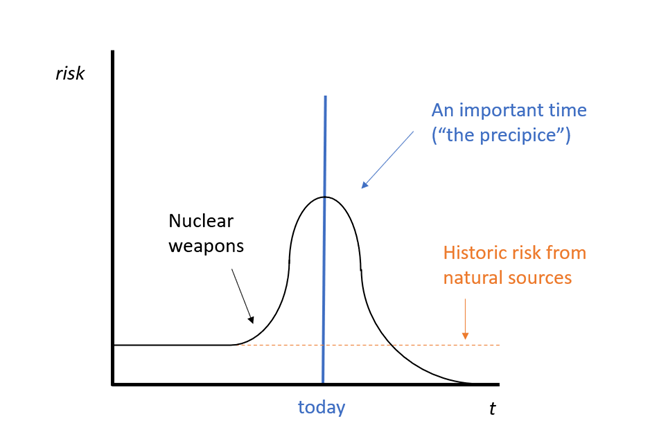
Whether the catastrophe rate trends towards zero over time depends on underlying dynamics. For natural risks, it’s plausible that we can build resilience that eliminates such risk. For example, the risk from an asteroid hitting earth causing an extinction-level event may be 1 in 1,000,000 this century[9]. Combining asteroid detection, the ability to potentially deflect asteroids, and the possibility of becoming a multi-planetary species, the risk of extinction from an asteroid could be ignored in the near future. For anthropogenic risks, on the other hand, many forces are likely to increase the level of risk, rather than decrease it.
Pressure on the catastrophe rate
For the sake of this argument, let’s consider four anthropogenic threats: nuclear war, pandemics (including bioterrorism), misaligned AI, and other risks.
The risk level from nuclear war has been much higher in the past that is now (e.g., during the cold war), and humanity has successfully built institutions and norms that to reduce the threat level. The risk could obviously be reduced much more, but this illustrates that we can act now to reduce risks. (Increased intentional cooperation may also reduce the risk of great power war occurring, which would exacerbate risks from nuclear war, and possibly other threats.)
This story represents something of a best-case scenario for an existential risk, but it’s possible risk profiles from other threats follow similar paths. Risks from pandemics, for example, could be greatly reduced by a combination of international coordination (e.g., norms against gain-of-function research), and technological advancement (e.g., better hazmat suits, and bacteria-killing lights[10]).
Both examples show how we can act to reduce the catastrophe rate over time, but there are also 3 key risk factors applying upward pressure on the catastrophe rate:
- The lingering nature of present threats
- Our ongoing ability to generate new threats
- Continuously lowering barriers to entry/access
In the case of AI, its usually viewed that AI will be aligned or misaligned, meaning this risk is either be solved or not. It’s also possible that AI may be aligned initially, and become misaligned later[11]. The need for ongoing protection from bad AI would therefore be ongoing. In this scenario we’d need systems in place to stop AI being misappropriated or manipulated, similar to how we guard nuclear weapons from dangerous actors. This is what I term “lingering risk”.
Nuclear war, pandemic risk, and AI risk are all threats that have emerged recently. Because we know them, it’s easier to imagine how we might navigate them. Other risks, however, are impossible to define because they don’t exist yet. Given the number of existential threats to have emerged in merely the last 100 years, it seems reasonable to think many more will come. It is difficult to imagine many future centuries of sustained technological development (i.e., the longtermist vision) occurring without humanity generating many new threats (on purpose or accidentally).
Advances in biotechnology have greatly increased the risk of engineered pandemics (by CRISPR). By reducing the barriers to entry, it is now cheaper and easier to develop dangerous technologies. I expect this trend to continue, and across many domains. The risks from continuously lowering barriers to entry also interacts with the previous 2 risk factors, meaning that lingering threats may become more unstable over time, and new threats inevitably become more widely accessible. Again, I would argue that the ongoing progress of science and technology, combined with trends making information more accessible, make opposition to this view incompatible with future centuries of science and technological development.
Given these 3 risk factors, one could easily argue the catastrophe rate is likely to increase over time, though I believe this may be too pessimistic. We only need to accept the discount rate is above zero for this to have profound implications. (As stated above, any positive rate “eventually wins.”)
While in reality the long-term catastrophe rate will fluctuate, I think it fair to assume it is constant (an average of unknowable fluctuations), and it is lower than the current catastrophe rate (partially accepting the premise we are at a precipice of sorts).
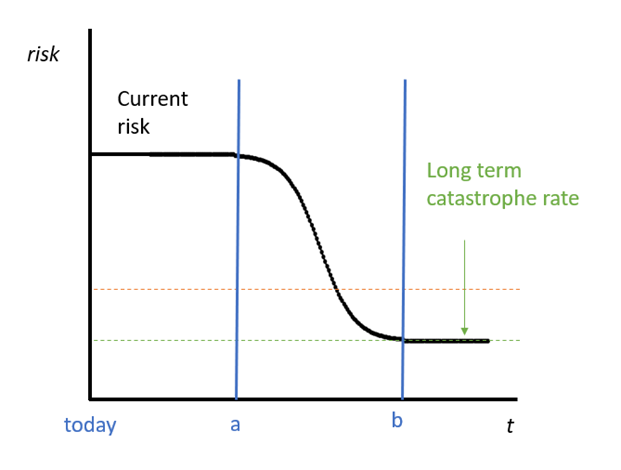
Finally, given the unknown trajectory of the long-term catastrophe rate (including the mere possibility that it may increase), we should assume it is inelastic, meaning our actions are unlikely to significantly affect it. (I do not believe this is true for the near-term rate).
Implication 1: We can only affect the near-term rate.
Efforts to reduce existential risk should be evaluated based on their impact on the expected value of humanity. The expected value of humanity (), defined by the number of people born each year (), and the probability of humanity existing in each year () can be calculated as follows:
where , otherwise:
,
where is the catastrophe rate each year. (The expected length of human existence can be calculated by substituting the number of people born each year for 1.)
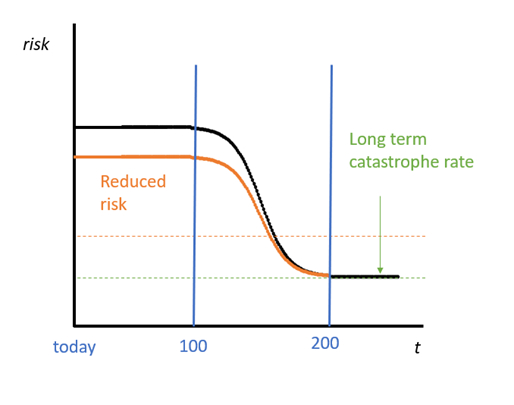
If the long-term catastrophe rate is fixed, we still can increase the expected value of humanity by reducing the near-term catastrophe rate. For simplicity, I suggest that the near-term rate applies for the next 100 years, decreases over the subsequent 100 years[12], then settles on long-term catastrophe rate is achieved in year 200, where it remains thereafter.
What is the long-term rate?
Toby Ord estimates the current risk per century is around 1 in 6[13]. If we do live in a time with an unusually high level of risk, we can treat this century as a baseline, and instead ask “how much more dangerous is our present century than the long-run average?” If current risks are twice as high as the long-run average, we would apply a long-term catastrophe rate of 1 in 12 (per century). Given the risk factors I described above (and the possibility the present is not unusually risky, but normal) it would be unrealistic to argue that present-day risks are any greater than 10 times higher than usual[14]. This suggest a long-term catastrophe rate per year of 1 in 10,000[15].
If the current risk settles at the long-run rate in 200 years, the expected length of human existence is another 8,200 years. This future contains an expected 1,025 billion people[16]. This is dramatically less than other widely cited estimates of humanity’s potential[17].
Humanity’s potential is vast, but introducing a discount rate reduces that potential to a much smaller expected value. If existential risk is an ever-present threat, we should consider the possibility that our existence is far less than the average mammalian species[18]. This might not be surprising, as we are clearly an exceptional species in so many other ways. And a short horizon would make sense, given the fermi paradox.
Other reasons for a zero rate
Another possible reason to argue for a zero-discount rate is that the intrinsic value of humanity increases at a rate greater than the long-run catastrophe rate[19]. This is wrong for (at least) 2 reasons.
First, this would actually imply a negative discount rate, and applying this rate over long periods of time could lead to the same radical conclusions I described above, however this time it would rule in favour of people in the future. Second, while it is true that lives lived today are much better than lives lived in the past (longer, healthier, richer), and the same may apply to the future, this logic leads to some deeply immoral places. The life of a person a who will live a long, healthy, and rich life, is worth no more than the life of the poorest, sickest, person alive. While some lives may be lived better, all lives are worth the same. Longtermism should accept this applies across time too.
Implication 2: Saving a single life in the present day[20]
Future people matter, there could be a lot of them, and they are overlooked. The actions we take now could ensure these people live, or don’t. This applies to humanity, but also to humans. If we think about an individual living in sub-Saharan Africa, every mosquito is in fact an existential risk to their future descendants.
Visualizations of humanities vast potential jump straight to a constant population, ignoring the fact that the population is an accumulation of billions of people’s individual circumstances. Critically, one person living does not cause another person to die[21], so saving one person saves many more people over the long course of time. Introducing a non-zero discount rate allows us to calculate a persons’ expected number of descendants ():
Under a stable future population, where people produce (on average) only enough offspring to replace themselves, a person’s expected number of descendants is equal to the expected length of human existence, divided by the average lifespan (). I estimate this figure is 93[22].
To be consistent, when comparing lives saved in present day interventions with (expected) lives saved from reduced existential risk, present day lives saved should be multiplied by this constant, to account for the longtermist implications of saving each person. This suggests priorities such as global health and development may be undervalued at present.
(Note that could be adjusted to reflect fertility, or gender, though I deliberately to ignore these because it they could dramatically, and immorally, overvalue certain lives relative to others[23].)
Does this matter?
At this point it’s worth asking exactly how much the discount rate matters. Clearly, its implications are very important for longtermism, but how important is longtermism to effective altruism? While longtermism has been getting a lot of media attention lately, and appears to occupy a very large amount of the “intellectual space” around the EA community, longtermist causes represent only about a quarter of the overall EA portfolio[24].
That said, longtermism does matter, a lot, because of the views of some of EAs biggest funders. People allocating large quantities of future funding between competing global priorities endorse longtermism, so the future EA portfolio might look very different to the current one. Sam Bankman-Fried recently said that near-term causes (such as global health and poverty) are “more emotionally driven[25]”. It’s a common refrain from longtermists, claiming to occupy the unintuitive moral high ground, because they have “done the math”. If my points above are above are correct, it's possible they have done the math wrong, underweighting many “emotionally driven” causes.
Conclusion
Any non-zero discount rate has profound implications for the expected value of humanity, reducing it from potentially infinity to a much lower value. If we cannot affect the long-term catastrophe rate, the benefits from reducing existential risk are only realised in the near future. This does not mean reducing existential risks are unimportant, my goal is to promote a more nuanced framework for evaluating the benefits of reducing existential risk. This framework directly implies we are undervaluing the present, and unequally applying longtermist principles only to existential risks, ignoring the longtermist consequences of saving individuals in the preset day.
EDITS
There are 3 points I should have made more clearly in the post above. Because they were not made in my original submission, I'm keeping them separate:
- My discount rate could be far too high (or low), but my goal is to promote existed value approaches for longtermism, not my own (weak) risk estimates.
- If my discount rate is too high, this would increase each individuals expected number of descendants, which makes this point robust to the actual value of the discount rate applied over time.
- I dismissed the "abstract value of humanity" as nonsense, which harsh, and it was cowardly doing it in a footnote. There is clearly some truth in the idea, but, what is the value of the last 10,000 people in existence, relative to the value of the last 1 million people in existence? Is it 1%, or is it 99.9%? The value must lie somewhere in between. What about the single last person, relative to the last 10? Unless we can define values like these, we should not use the abstract value of humanity to prioritize certain causes when equally assessing the longtermist consequences of extinction and individual death.
- ^
- ^
- ^
- ^
1,000,000 / 1.01^1,500 = 0.330
- ^
- ^
The Precipice, Toby Ord
- ^
Particularly appendix A (discounting the future)
- ^
Under the precipice view, we should technically discount the next few centuries according to the catastrophe rate, but because the catastrophe rate is forecast to decreases to zero eventually, the future afterwards is infinite, making the initial period redundant.
- ^
Table 6.1: The Precipice, Toby Ord
- ^
Will MacAskill, every recent podcast episode (2022)
- ^
Speculative, outside my domain.
- ^
In my calculations I model the change from year 100 to 200 with a sigmoid curve (k=0.2).
- ^
Table 6.1: The Precipice, Toby Ord
- ^
Of course, I accept this is highly subjective.
- ^
Using a lower estimate of the current risk, the risk of catastrophe per year is 1 in 1087 (this accumulates to 1 in ~10 over 100 years). My calculations can be found here: https://paneldata.shinyapps.io/xrisk/
- ^
A stable population of 11 billion people living to 88 years implies 125m people are born (and die) each year.
- ^
- ^
Estimates range from 0.6m to 1.7m years: https://ourworldindata.org/longtermism
- ^
Appendix E, The Precipice.
- ^
This clearly ignores the value of “humanity” in the abstract sense, but frankly, this is hippy nonsense. For our purposes, the value of humanity today should be roughly equal to 8 billion times the value of 1 person.
- ^
In other words, Malthus was wrong about population growth.
- ^
8,200 years (see above) divided by average lifespan (88 years).
- ^
This magnitude of these factors could be greater than age differences inferred using DALYs.
- ^
- ^

It's quite likely the extinction/existential catastrophe rate approaches zero within a few centuries if civilization survives, because:
If we're more than 50% likely to get to that kind of robust state, which I think is true, and I believe Toby does as well, then the life expectancy of civilization is very long, almost as long on a log scale as with 100%.
Your argument depends on 99%+++ credence that such safe stable states won't be attained, which is doubtful for 50% credence, and quite implausible at that level. A classic paper by the climate economist Martin Weitzman shows that the average discount rate over long periods is set by the lowest plausible rate (as the possibilities of high rates drop out after a short period and you get a constant factor penalty for the probability of low discount rates, not exponential decay).
Not really disagreeing with anything you've said, but I just wanted to point out that this sentence doesn't quite acknowledge the whole story. To quote from Hilary Greaves' "Discounting for public policy: A survey" paper:
The link you just posted seems broken? Hilary Greaves' Discounting for public policy: A survey is available in full at the following URL.
This seems like an important claim, but I could also quite plausibly see misaligned AIs destabilising a world where an aligned AI exists. What reasons do we have to think that an aligned AI would be able to very consistently (e.g. 99.9%+ of the time) ward off attacks from misaligned AI from bad actors? Given all the uncertainty around these scenarios, I think the extinction risk per century from this alone could in the 1-5% range and create a nontrivial discount rate.
Today there is room for an intelligence explosion and explosive reproduction of AGI/robots (the Solar System can support trillions of AGIs for every human alive today). If aligned AGI undergoes such intelligence explosion and reproduction there is no longer free energy for rogue AGI to grow explosively. A single rogue AGI introduced to such a society would be vastly outnumbered and would lack special advantages, while superabundant AGI law enforcement would be well positioned to detect or prevent such an introduction in any case.
Already today states have reasonably strong monopolies on the use of force. If all military equipment (and an AI/robotic infrastructure that supports it and most of the economy) is trustworthy (e.g. can be relied on not to engage in military coup, to comply with and enforce international treaties via AIs verified by all states, etc) then there could be trillions of aligned AGIs per human, plenty to block violent crime or WMD terrorism.
For war between states, that's point #7. States can make binding treaties to renounce WMD war or protect human rights or the like, enforced by AGI systems jointly constructed/inspected by the parties.
One possibility would be that these misaligned AIs are quickly defeated or contained, and future ones are also severely resource-constrained by the aligned AI, which has a large resource advantage. So there are possible worlds where there aren't really any powerful misaligned AIs (nearby), and those worlds have vast futures.
What would be the per-century risk in such a state?
Also, does the >50% of such a state account for the possibility of alien civilizations destroying us or otherwise limiting our expansion?
Barring simulation shutdown sorts of things or divine intervention I think more like 1 in 1 million per century, on the order of magnitude of encounters with alien civilizations. Simulation shutdown is a hole in the argument that we could attain such a state, and I think a good reason not to say things like 'the future is in expectation 50 orders of magnitude more important than the present.'
Whether simulation shutdown is a good reason not to say such things would seem to depend on how you model the possibility of simulation shutdown.
One naive model would say that there is a 1/n chance that the argument that such a risk exists is correct, and if so, there is 1/m annual risk, otherwise, there is 0 annual risk from simulation shutdown. In such a model, the value of the future endowment would only be decreased n-fold. Whereas if you thought that there was definitely a 1/(mn) annual risk (i.e. the annual risk is IID) then that risk would diminish the value of the cosmic endowment by many OoM.
I'd use reasoning like this, so simulation concerns don't have to be ~certain to drastically reduce EV gaps between local and future oriented actions.
What is the source of the estimate of the frequency of encounters with alien civilizations?
Here's a good piece.
Could you say more about what you mean by this?
[Epistemic status: I have just read the summary of the post by the author and by Zoe Williams]
Doesn't it make more sense to just set the discount rate dynamically accounting for the current (at the present) estimations?
If/when we reach a point where the long-term existential catastrophe rate approaches zero, then it will be the moment to set the discount rate to zero. Now it is not, so the discount rate should be higher as the author proposes.
Is there a reason for not using in a dynamic discount rate?
If you think the annual rate of catastrophic risk is X this century but only 0.5X next century, 0.25X the century afterwards etc, then you'd vastly underestimate expected value of the future if you use current x-risk levels to set the long-term discount rate.
Whether this is practically relevant or not is of course significantly more debatable.
But the underestimation would be temporal.
I'm also not clear on whether this is practically relevant or not.
Related and see also the discussion: https://forum.effectivealtruism.org/posts/N6hcw8CxK7D3FCD5v/existential-risk-pessimism-and-the-time-of-perils-4
I don't think this is an innocuous assumption! Long term anthropogenic risk is surely a function of technological progress, population, social values, etc - all of which are trending, not just fluctuating. So it feels like catastrophe rate should also be trending long term.
This seems like an important response: you should have uncertainty about the per-century discount rate, and worlds where it's much lower have much vaster futures. You should fix each per-century discount rate (or per-century discount rate trajectory), get an estimate over the size of the future, and then take the expected value of the size of the future over your distribution of per-century discount rates (or discount rate trajectories).
See https://forum.effectivealtruism.org/posts/XZGmc5QFuaenC33hm/cross-post-a-nuclear-war-forecast-is-not-a-coin-flip
It could still be case that we should be very confident that it's not extremely low, and so those worlds don't contribute much, or giving them too much weight is Pascalian. But I think that takes a stronger argument.
Thanks for posting this! Do you have a take on Tarsney's point about uncertainty in model parameters in the paper you cite in your introduction? Quoting from his conclusions (though there's much more discussion earlier):
Space colonization could continually decrease the future risk of extinction by reducing correlations in extinction events across distant groups. This is assuming we don't encounter grabby aliens.
I just want to flag one aspect of this I haven't seen mentioned, which is that much of this lingering risk naturally grows with population, since you have more potential actors. If you have acceptable risk per century with 10 BSL-4 labs, the risk with 100 labs might be too much. If you have acceptable risk with one pair of nuclear rivals in cold war, a 20-way cold war could require much heavier policing to meet the same level of risk. I expanded on this in a note here.
Thank you for your thoughts, and welcome to the forum! I recently posted my first post as well, which was on the same issue (although approached somewhat differently) It is at https://forum.effectivealtruism.org/posts/xvsmRLS998PpHffHE/concerns-with-longtermism. I have other concerns as well with longtermism, even though, like you, I certainly recognize that we need to take future outcomes into account. I hope to post one of those soon. I would welcome your thoughts.
You write:
Your footnote is to The Precipice: To quote from The Precipice Appendix E:
Regarding your first reason: You first cite that this would imply a negative-discount rate that rules in favor of future people; I'm confused why this is bad? You mention "radical conclusions" – I mean sure, there are many radical conclusions in the world, for instance I believe that factory farming is a moral atrocity being committed by almost all of current society – that's a radical view. Being a radical view doesn't make it wrong (although I think we should be healthily skeptical of views that seem weird). Another radical conclusion I hold is that all people around the world are morally valuable, and enslaving them would be terrible; this view would appear radical to most people at various points in history, and is not radical in most the world now.
Regarding your second reason:
I would pose to you the question: Would you rather give birth to somebody who would be tortured their entire life or somebody who would be quite happy throughout their life (though they experience ups and downs)? Perhaps you are indifferent between these, but I doubt it (they both are one life being born, however, so taking the "all lives are worth the same" line literally here implies they are equally good). I think the value of a future where everybody being tortured is quite bad and is probably worse than extinction, whereas a flourishing future where people are very happy and have their needs met would be awesome!
I agree that there are some pretty unintuitive conclusions of this kind of thinking, but there are also unintuitive conclusions if you reject it! I think the value of an average life today, to the person living it, is probably higher than the value of an average life in 1700 CE, to the person living it. In the above Precipice passage, Ord discusses some reasons why this might be so.
Welcome to the forum! I am glad that you posted this! And also I disagree with much of it. Carl Shulman already responded explaining why he things the extinction rate approaches zero fairly soon, reasoning I agree with.
I think the assumption about a stable future population is inconsistent with your calculation of the value of the average life. I think of two different possible worlds:
World 1: People have exactly enough children to replace themselves, regardless of the size of the population. The population is 7 billion in the first generation; a billion extra (not being accounted for in the ~2.1 kids per couple replacement rate) people die before being able to reproduce. The population then goes on to be 6 billion for the rest of the time until humanity perishes. Each person who died cost humanity 93 future people, making their death much worse than without this consideration.
World 2: People have more children than replace themselves, up to the point where the population hits the carrying capacity (say it's 7 billion). The population is 7 billion in the first generation; a billion extra (not being accounted for in the ~2.1 kids per couple replacement rate) people die before being able to reproduce. The population then goes on to be 6 billion for one generation, but the people in that generation realize that they can have more than 2.1 kids. Maybe they have 2.2 kids, and each successive generation does this until the population is back to 7 billion (the amount of time this takes depends on numbers, but shouldn't be more than a couple generations).
World 2 seems much more realistic to me. While in World 1, each death cost the universe 1 life and 93 potential lives, in World 2 each death cost the universe something like 1 life and 0-2 potential lives.
It seems like using an average number of descendants isn't the important factor if we live in a world like World 2 because as long as the population isn't too small, it will be able to jumpstart the future population again. Thus follows the belief that (100% of people dying vs. 99% of people dying) is a greater difference than (0% of people dying vs. 99% of people dying). Assuming 1% of people would be able to eventually grow the population back.