S-risks, X-risks, and Ideal Futures

OscarD🔸

Following Ord (2023) I define the total value of the future as

where $τ$ is the length of time until extinction and $v (t)$ is the instantaneous value of the world at time $t$ . Of course, we are uncertain what value V will take, so we should consider a probability distribution of possible values of V.^[1] On the y-axis in the following graphs is probability density, and on the x-axis is a pseudo-log transformed version of V that allows V to vary by sign and over many OOMs on the same axis.^[2]

There are infinite possible distributions we may believe, but we can tease out some important distinguishing features of distributions of V, and map these onto plausible longtermist prioritisations of how to improve the future.

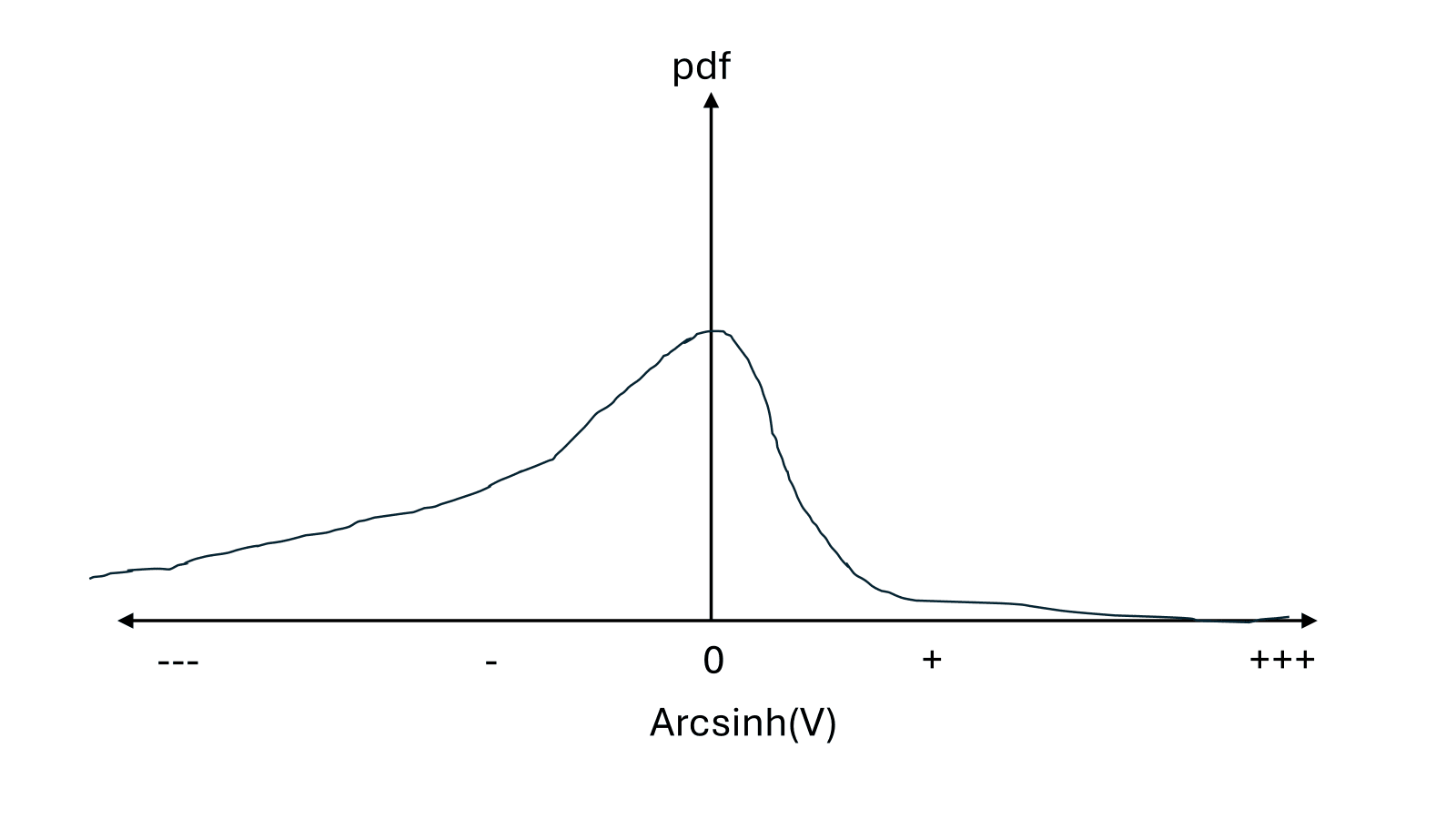
S-risk focused

If there is a significant chance of very bad futures (S-risks), then making those futures either less likely to occur, or less bad if they do occur seems very valuable, regardless of the relative probability of extinction versus nice futures.

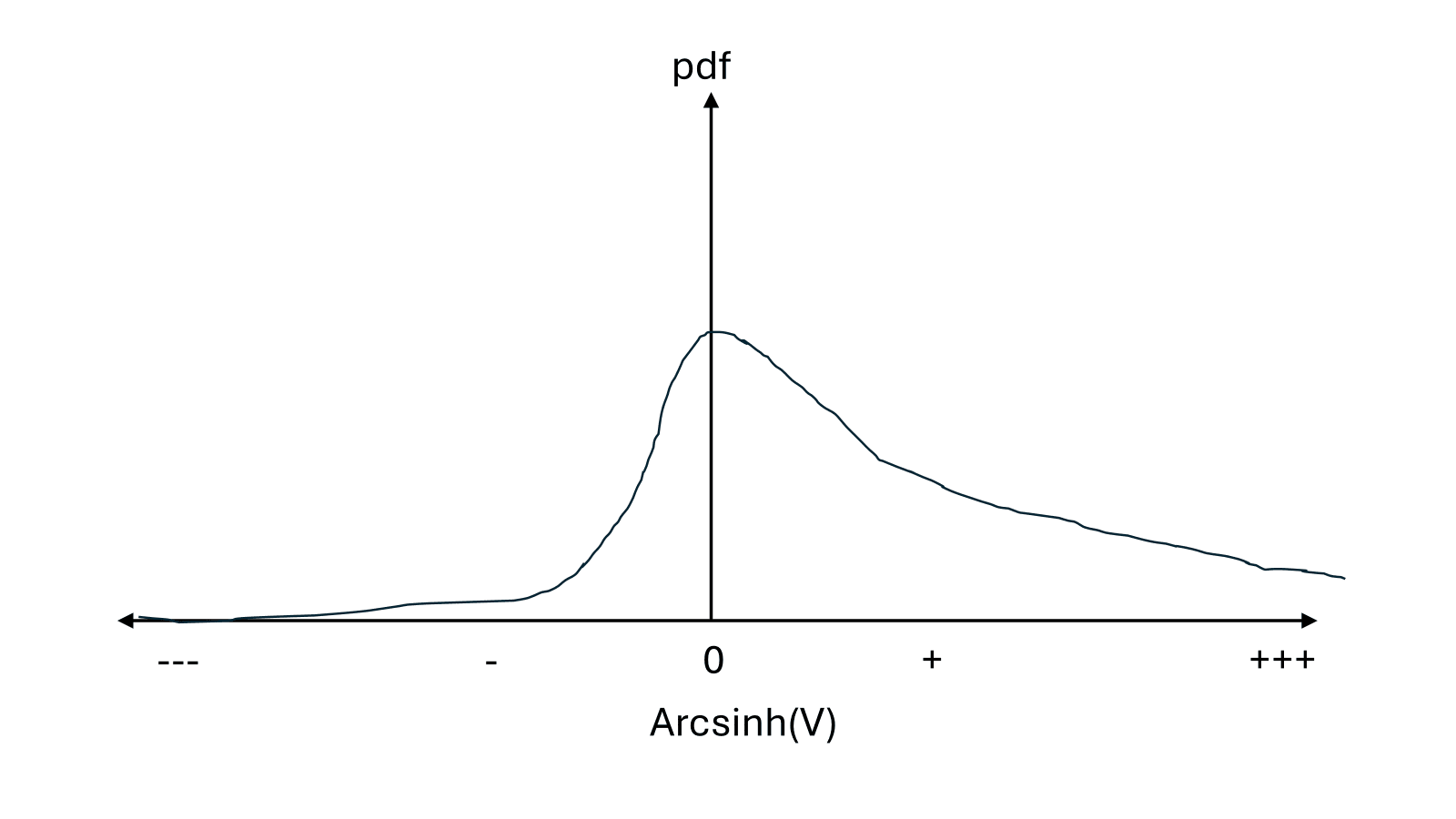
Ideal-future focused

If bad futures are very unlikely, and there is a very high variance in just how good positive futures are, then moving probability mass from moderately good to astronomically good futures could be even more valuable than moving probability mass from extinction to moderately good futures (keeping in mind the log-like transformation of the x-axis).

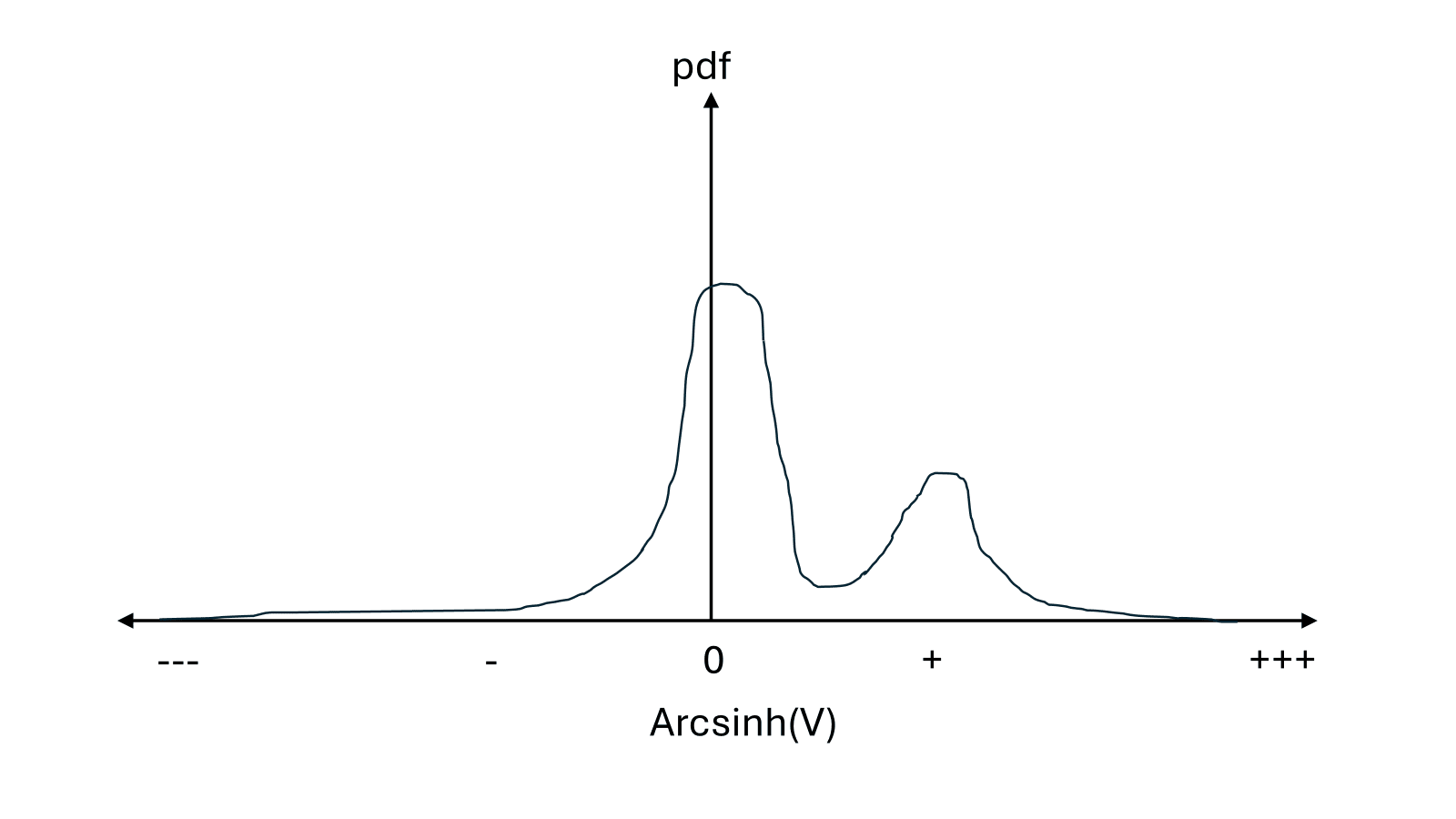
X-risk focused

If there is a large probability of both near-term extinction and a good future, but both astronomically good and astronomically bad futures are ~impossible, then preventing X-risks (and thereby locking us into one of many possible low-variance moderately good futures) seems very important.

Discussion

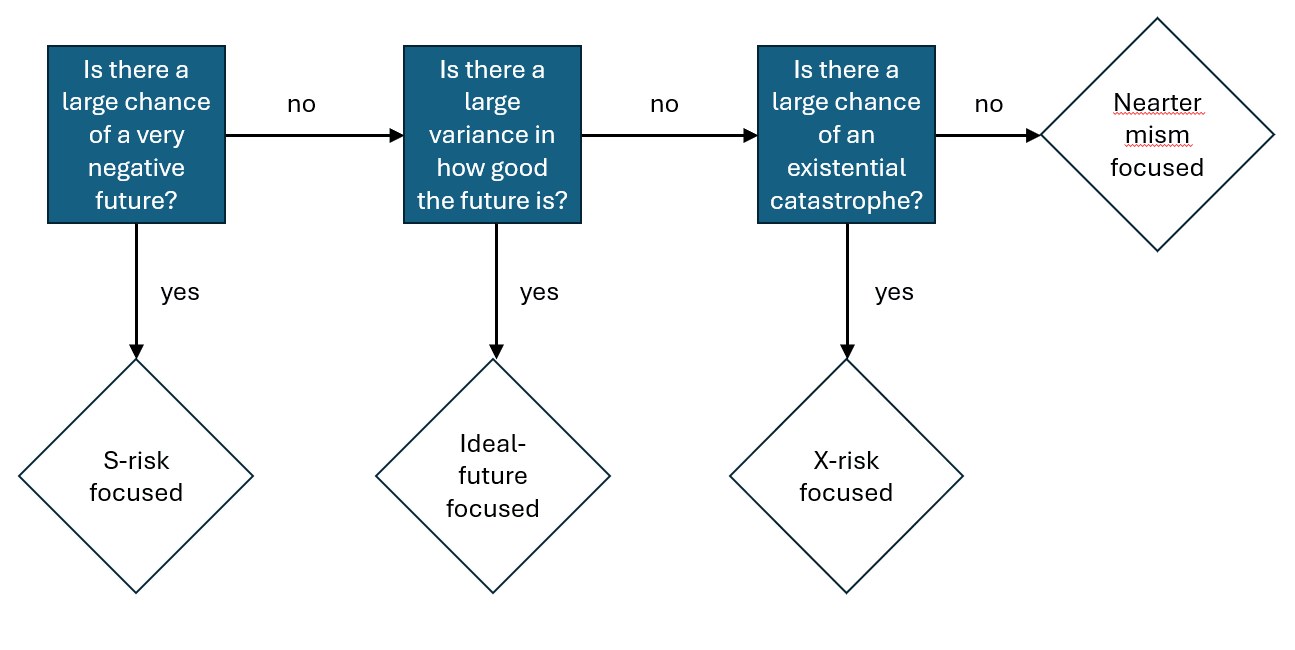
Some differences between these camps are normative, e.g. negative utilitarians are more likely to focus on S-risks, and person-affecting views are more likely to favour X-risk prevention over ensuring good futures are astronomically large. But significant prioritisation disagreement probably also arises from empirical disagreements about likely future trajectories, as stylistically represented by my three probability distributions. In flowchart form this is something like:
I have not encountered particularly strong arguments about what sort of distribution we should assign to V - my impression is that intuitions (implicit Bayesian priors) are doing a lot of the work, and it may be quite hard to change someone’s mind about the shape of this distribution. But I think explicitly describing and drawing these distributions can be useful in at least understanding our empirical disagreements.
I don’t have any particular conclusions, I just found this a helpful framing/visualisation for my thinking and maybe it will be for others too.

^{^}
None of the ideas in this post are particularly original (see e.g. Beckstead and Bostrom here and Harling here). I haven't seen graphs quite like this presented before, but it is a simple visualisation so quite possibly others have done this before too!
^{^}
For the mathematicians among us, let’s use arcsinh(V), which is like a log scaling, but crucially allows for negative values as well. For small values of V, arcsinh(V) ~V, and for large values of V, arcsinh(V) ~ sign(V) * log|2V|, with nice smooth transitions between these regimes (desmos).

15 Reactions

Comments6

Sorted by

New & upvoted

Click to highlight new comments since: Today at 10:39 PM

[anonymous]Jun 189

I don't think that high x-risk implies that we should focus more on x-risk all else equal - high x-risk means that the value of the future is lower. I think what we should care about is high tractability of x-risk, which sometimes but doesn't necessarily correspond to a high probability of x-risk.

OscarD🔸Jun 181

Good point, I think if X-risk is very low it is less urgent/important to work on (so the conditional works in that direction I reckon). But I agree that the inverse - if X-risk is very high, it is very urgent/important to work on - isn't always true (though I think it usually is - generally bigger risks are easier to work on).

David MJun 183

I think high X-risk makes working on X-risk more valuable only if you believe that you can have a durable effect on the level of X-risk - here's MacAskill talking about the hinge-of-history hypothesis (which is closely related to the 'time of perils' hypothesis):

Or perhaps extinction risk is high, but will stay high indefinitely, in which case in expectation we do not have a very long future ahead of us, and the grounds for thinking that extinction risk reduction is of enormous value fall away.

Vasco Grilo🔸Jun 192

Hi Oscar,

I would be curious to know your thoughts on my post Reducing the nearterm risk of human extinction is not astronomically cost-effective? (feel free to comment there).

Summary
I believe many in the effective altruism community, including me in the past, have at some point concluded that reducing the nearterm risk of human extinction is astronomically cost-effective. For this to hold, it has to increase the chance that the future has an astronomical value, which is what drives its expected value.
Nevertheless, reducing the nearterm risk of human extinction only obviously makes worlds with close to 0 value less likely. It does not have to make ones with astronomical value significantly more likely. A priori, I would say the probability mass is moved to nearby worlds which are just slightly better than the ones where humans go extinct soon. Consequently, interventions reducing nearterm extinction risk need not be astronomically cost-effective.
I wonder whether the conclusion that reducing the nearterm risk of human extinction is astronomically cost-effective may be explained by:
Authority bias, binary bias and scope neglect.
Little use of empirical evidence and detailed quantitative models to catch the above biases.

OscarD🔸Jun 243

Thanks, interesting ideas. I overall wasn't very persuaded - I think if we prevent an extinction event in the 21st century, the natural assumption is that probability mass is evenly distributed over all other futures, and we need to make arguments in specific cases as to why this isn't the case. I didn't read the whole dialogue but I think I mostly agree with Owen.

Vasco Grilo🔸Jun 242

I think if we prevent an extinction event in the 21st century, the natural assumption is that probability mass is evenly distributed over all other futures, and we need to make arguments in specific cases as to why this isn't the case.

I make some specific arguments:

As far as I can tell, the (posterior) counterfactual impact of interventions whose effects can be accurately measured, like ones in global health and development, decays to 0 as time goes by, and can be modelled as increasing the value of the world for a few years or decades, far from astronomically.
[...]
Here are some intuition pumps for why reducing the nearterm risk of human extinction says practically nothing about changes to the expected value of the future. In terms of:
Human life expectancy:
I have around 1 life of value left, whereas I calculated an expected value of the future of 1.40*10^52 lives.
Ensuring the future survives over 1 year, i.e. over 8*10^7 lives (= 8*10^(9 - 2)) for a lifespan of 100 years, is analogous to ensuring I survive over 5.71*10^-45 lives (= 8*10^7/(1.40*10^52)), i.e. over 1.80*10^-35 seconds (= 5.71*10^-45*10^2*365.25*86400).
Decreasing my risk of death over such an infinitesimal period of time says basically nothing about whether I have significantly extended my life expectancy. In addition, I should be a priori very sceptical about claims that the expected value of my life will be significantly determined over that period (e.g. because my risk of death is concentrated there).
Similarly, I am guessing decreasing the nearterm risk of human extinction says practically nothing about changes to the expected value of the future. Additionally, I should be a priori very sceptical about claims that the expected value of the future will be significantly determined over the next few decades (e.g. because we are in a time of perils).
A missing pen:
If I leave my desk for 10 min, and a pen is missing when I come back, I should not assume the pen is equally likely to be in any 2 points inside a sphere of radius 180 M km (= 10*60*3*10^8) centred on my desk. Assuming the pen is around 180 M km away would be even less valid.
The probability of the pen being in my home will be much higher than outside it. The probability of being outside Portugal will be negligible, but the probability of being outside Europe even lower, and in Mars even lower still^[5].
Similarly, if an intervention makes the least valuable future worlds less likely, I should not assume the missing probability mass is as likely to be in slightly more valuable worlds as in astronomically valuable worlds. Assuming the probability mass is all moved to the astronomically valuable worlds would be even less valid.
Moving mass:
For a given cost/effort, the amount of physical mass one can transfer from one point to another decreases with the distance between them. If the distance is sufficiently large, basically no mass can be transferred.
Similarly, the probability mass which is transferred from the least valuable worlds to more valuable ones decreases with the distance (in value) between them. If the world is sufficiently faraway (valuable), basically no mass can be transferred.