Summary
Most moral impact estimates and cost-effectiveness analyses in the effective altruism community use (differences in) expected total welfare. However, doing so generally is probably irrational, based on arguments related to St Petersburg game-like prospects. These are prospects that are strictly better than each of their infinitely many possible but finite actual value outcomes, with unbounded but finite value across these outcomes. The arguments I consider here are:
- Based on a money pump argument, the kind used to defend the axioms of expected utility theory, maximizing the expected value of an unbounded utility function is irrational. As a special case, expectational total utilitarianism, i.e. maximizing the expected value of total welfare, is also irrational.
- Two recent impossibility theorems demonstrate the incompatibility of Stochastic Dominance — a widely accepted requirement for instrumental rationality — with Impartiality and each of Anteriority and Separability. These last three principles are extensions of standard assumptions used in theorems to prove utilitarianism, e.g. Anteriority in Harsanyi's theorem.
Taken together, utilitarianism is either irrational or the kinds of arguments used to support it in fact undermine it instead when generalized. However, this doesn't give us any positive arguments for any other specific views.
I conclude with a discussion of responses.
EDIT: I've rewritten the summary and the title, and made various other edits for clarity and to better motivate. The original title of this post was "Utilitarianism is irrational or self-undermining".
Basic terminology
By utilitarianism, I include basically all views that are impartial and additive in deterministic fixed finite population cases. Some such views may not be vulnerable to all of the objections here, but they apply to most such views I’ve come across, including total utilitarianism. These problems also apply to non-consequentialists using utilitarian axiologies.
To avoid confusion, I prefer the term welfare as what your moral/social/impersonal preferences and therefore what your utility function should take into account.[1] In other words, your utility function can be a function of individuals’ welfare levels.
A prospect is a probability distribution over outcomes, e.g. over heads or tails from a coin toss, over possible futures, etc..
Motivation and outline
Many people in the effective altruism and rationality communities seem to be expectational total utilitarians or give substantial weight to expectational total utilitarianism. They take their utility function to just be total welfare across space and time, and so aim to maximize the expected value of total welfare (total individual utility), . Whether or not committed to expectational total utilitarianism, many in these communities also argue based on explicit estimates of differences in expected total welfare. Almost all impact and cost-effectiveness estimation in the communities is also done this way. These arguments and estimation procedures agree with and use expected total welfare, but if there are problems with expectational total utilitarianism in general, then there’s a problem with the argument form and we should worry about specific judgements using it.
And there are problems.
Total welfare, and differences in total welfare between prospects, may be unbounded, even if it were definitely finite. We shouldn't be 100% certain of any specified upper bound on how long our actions will affect value in the future, or even for how long a moral patient can exist and aggregate welfare over their existence. By this, I mean that you can't propose some finite number such that your impact must, with 100% probability, be at most . doesn't have to be a tight upper bound. Here are some arguments for this:
- Given any proposed maximum value, we can always ask: isn't there at least some chance it could go on for 1 second more? Even if extremely tiny. By induction, we'll have to go past any .[2]
- How would you justify your choice of and 100% certainty in it? (Feel free to try, and I can try to poke holes in the argument.)
- You shouldn't be 100% certain of anything, except maybe logical necessities and/or some exceptions with continuous distributions (Cromwell's rule).
- If you grant any weight to the views of those who aren't 100% sure of any specific finite upper bound, then you also shouldn't be 100% sure of any, either. If you don't grant any weight to them, then this is objectionably epistemically arrogant. For a defense of epistemic modesty, see Lewis, 2017.
- There are some specific possibilities allowing this that aren't ruled out by models of the universe consistent with current observations, like creating more universes, from which other universes can be created, and so on (Tomasik, 2017).
We could also have no sure upper bound on the spatial size of the universe or the number of moral patients around now.[3] Now, you might say you can just ignore everything far enough away, because you won't affect it. If your decisions don't depend on what's far enough away and unaffected by your actions, then this means, by definition, satisfying a principle of Separability. But then you're forced to give up impartiality or one of the least controversial proposed requirements of rationality, Stochastic Dominance. I'll state and illustrate these definitions and restate the result later, in the section Anti-utilitarian theorems.
This post is concerned with the implications of prospects with infinitely many possible outcomes and unbounded but finite value, not actual infinities, infinite populations or infinite ethics generally. The problems arise due to St Petersburg-like prospects or heavy-tailed distributions (and generalizations[4]): prospects with infinitely many possible outcomes, infinite (or undefined) expected utility, but finite utility in each possible outcome. The requirements of rationality should apply to choices involving such possibilities, even if remote.
The papers I focus on are:
- Jeffrey Sanford Russell, and Yoaav Isaacs. “Infinite Prospects*.” Philosophy and Phenomenological Research, vol. 103, no. 1, Wiley, July 2020, pp. 178–98, https://doi.org/10.1111/phpr.12704, https://philarchive.org/rec/RUSINP-2
- Goodsell, Zachary. “A St Petersburg Paradox for Risky Welfare Aggregation.” Analysis, vol. 81, no. 3, Oxford University Press, May 2021, pp. 420–26, https://doi.org/10.1093/analys/anaa079, https://philpapers.org/rec/GOOASP-2
- Jeffrey Sanford Russell. “On Two Arguments for Fanaticism.” Noûs, Wiley-Blackwell, June 2023, https://doi.org/10.1111/nous.12461, https://philpapers.org/rec/RUSOTA-2, https://globalprioritiesinstitute.org/on-two-arguments-for-fanaticism-jeff-sanford-russell-university-of-southern-california/
Respectively, they:
- Argue that unbounded utility functions (and generalizations) are irrational (or at least as irrational as violating Independence or the Sure-Thing Principle, crucial principles for expected utility theory).
- Prove that Stochastic Dominance, Impartiality and Anteriority are jointly inconsistent.
- Prove that Stochastic Dominance, Compensation (which implies Impartiality) and Separability are jointly inconsistent.
Again, respecting Stochastic Dominance is among the least controversial proposed requirements of instrumental rationality. Impartiality, Anteriority and Separability are principles (or similarly motivated extensions thereof) used to support and even prove utilitarianism.
I will explain what these results mean, including a money pump for 1 in the correspondingly named section, and definitions, motivation and background for the other two in the section Anti-utilitarian theorems. I won't include proofs for 2 or 3; see the papers instead. Along the way, I will argue based on them that all (or most standard) forms of utilitarianism are irrational, or the standard arguments used in defense of principles in support of utilitarianism actually extend to principles that undermine utilitarianism. Then, in the last section, Responses, I consider some responses and respond to them.
Unbounded utility functions are irrational
Expected utility maximization with an unbounded utility function is probably (instrumentally) irrational, because it recommends, in some hypothetical scenarios, choices leading to apparently irrational behaviour. This includes foreseeable sure losses — a money pump —, and paying to avoid information, among others, following from the violation of extensions of the Independence axiom[5] and Sure-Thing Principle[6] (Russell and Isaacs, 2021, p.3-5).[7] The issue comes from St Petersburg game-like prospects: prospects with infinitely many possible outcomes, each of finite utility, but with overall infinite (or undefined) expected utility, as well as generalizations of such prospects.[4] Such a prospect is, counterintuitively, better than each of its possible outcomes.[8]
The original St Petersburg game is a prospect that with probability gives you , for each positive integer (Peterson, 2023). The expected payout from this game is infinite,[9] even though each possible outcome is finite. But it's not money we care about in itself.
Suppose you have an unbounded real-valued utility function .[4] Then it’s unbounded above or below. Assume it’s unbounded above, as a symmetric argument applies if it’s only unbounded below. Then, being unbounded above implies that it takes some utility value , and for each utility value , there’s some outcome such that . Then we can construct a countable sequence of outcomes, , with for each , as follows:
- Choose an outcome such that .
- Choose an outcome such that .
- …
- Choose an outcome such that .
- …
Define a prospect as follows: with probability . Then, ,[10] and is better than any prospect with finite expected utility.[11]
St Petersburg game-like prospects lead to violations of generalizations of the Independence axiom and the Sure-Thing Principle to prospects over infinitely (countably) many possible outcomes (Russell and Isaacs, 2021).[12] The corresponding standard finitary versions are foundational principles used to establish expected utility representations of preferences in the von Neumann-Morgenstern utility theorem (von Neumann and Morgenstern, 1944) and Savage’s theorem (Savage, 1972), respectively. The arguments for the countable generalizations are essentially the same as those for the standard finitary versions (Russell and Isaacs, 2021), and in the following subsection, I will illustrate one: a money pump argument. So, if money pumps establish the irrationality of violations of the standard finitary Sure-Thing Principle, they should too for the countable version. Then maximizing the expected value of an unbounded utility function is irrational.
A money pump argument
Consider the following hypothetical situation, adapted from Russell and Isaacs, 2021, but with a genie instead. It’s the same kind of money pump that would be used in support of the Sure-Thing Principle, and structurally nearly identical to the one to used to defend Independence in Gustafsson, 2022.
You are facing a prospect with infinite expected utility, but finite utility no matter what actually happens. Maybe is your own future and you value your years of life linearly, and could live arbitrarily but finitely long, and so long under some possibilities that your life expectancy and corresponding expected utility is infinite. Or, you're an expectational total utilitarian, and thinking about the value in distant parts of the universe (or multiverse), with infinite expected value but almost certainly finite.[13]
Now, there’s an honest and accurate genie — or God or whoever’s simulating our world or an AI with extremely advanced predictive capabilities — that offers to tell you exactly how will turn out.[14] Talking to them and finding out won’t affect or its utility, they’ll just tell you what you’ll get. The genie will pester you unless you listen or you pay them $50 to go away. Since there’s no harm in finding out, and no matter what happens, being an extra $50 poorer is worse, because that $50 could be used for ice cream or bed nets,[15] you conclude it's better to find out.
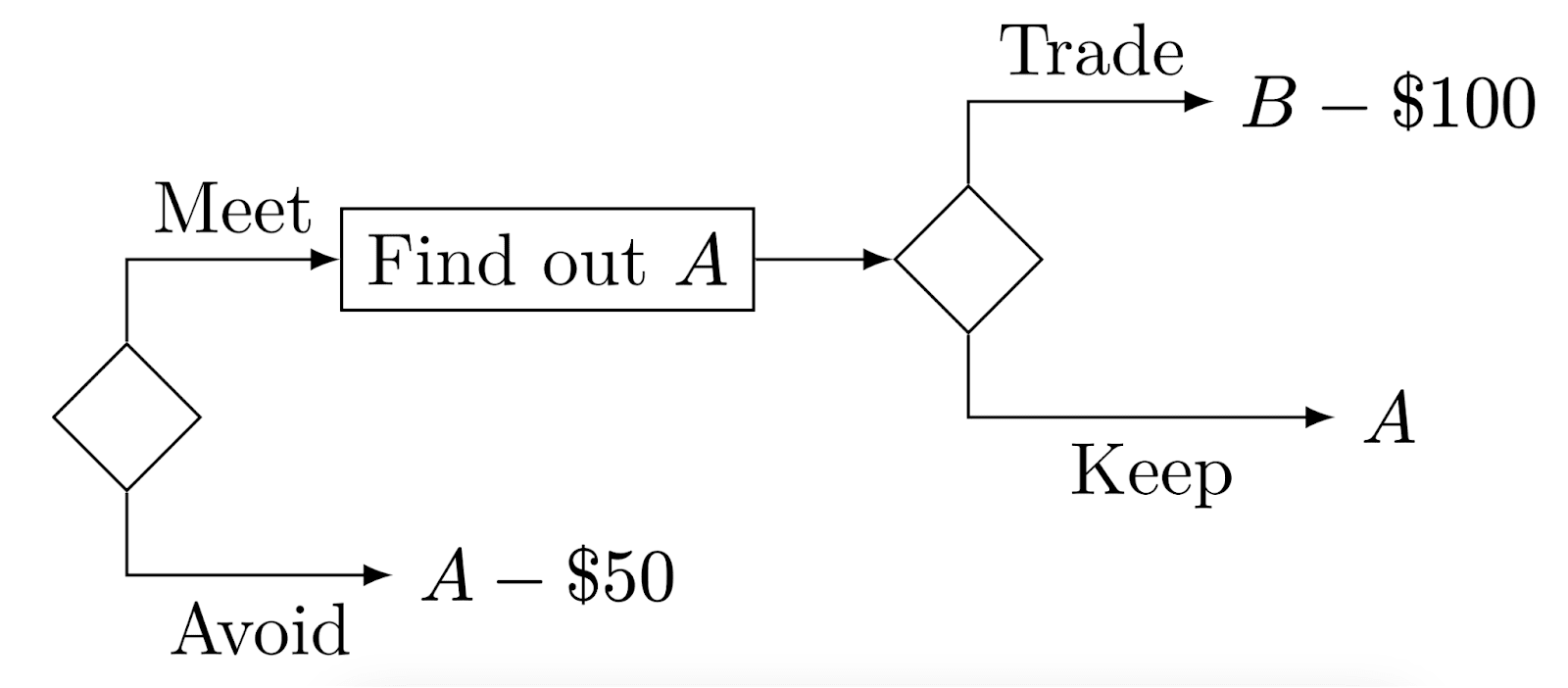
However, once you do find out, the result is, as you were certain it would be, finite. The genie turns out to be very powerful, too, and feeling generous, offers you the option to metaphorically reroll the dice. You can trade the outcome of for a new prospect with the same distribution as you had for from before you found out, but statistically independent from the outcome of . would have been equivalent, because the distributions would have been the same, but now looks better because the outcome of is only finite. But, you’d have to pay the genie $100 for . Still, $100 isn’t enough to drop the expected utility into the finite, and this infinite expected utility is much better than the finite utility outcome of . You could refuse, but it's a worthwhile trade to make, so you do it.
But then you step back and consider what you've just done. If you hadn't found out the value of , you would have stuck with it, since was better than - $100 ahead of time: was equivalent to a prospect, the prospect , that's certainly better than - $100. You would have traded the outcome of away for - $100 no matter what the outcome of would be, even though was better ahead of time than - $100. It was equivalent to , and - $100 is strictly worse, because it's the same but $100 poorer no matter what.
Not only that, if you hadn't found out the value of , you would have no reason to pay for . Even - $50 would have been better than - $100. Ahead of time, if you knew what the genie was going to do, but not the value of , ending up with - $100 would be worse than each of and - $50.
Suppose you're back at the start before knowing and with the genie pestering you to hear how it will turn out. Suppose you also know ahead of time that the genie will offer you for $100 no matter the outcome of , but you don't yet know how will turn out. Predicting what you'd do to respect your own preferences, you reason that if you find out , no matter what it is, you'd pay $100 for . In other words, accepting the genie's offer to find out actually means ending up with - $100 no matter what. So, really, accepting to find out from the genie just is - $100. But - $100 is also worse than - $50 (you're guaranteed to be $50 poorer than with - $50, which is equivalent to - $50). It would have been better to pay the genie $50 to go away without telling you how will go.
So this time, you pay the genie $50 to go away, to avoid finding out true information and making a foreseeably worse decision based on it. And now you're out $50, and definitely worse off than if you could have stuck through with , finding out its value and refusing to pay $100 to switch to . And you had the option to stick with though the whole sequence and could have, if only you wouldn't trade it away for at a cost of $100.
So, whatever strategy you follow, if constrained within the options I described, you will act irrationally. Specifically, either
- With nonzero probability, you will refuse to follow your own preferences when offered - $100 after finding out , which would be irrational then (Gustafsson, 2022 and Russell and Isaacs, 2021 argue similarly against resolute choice strategies). Or,
- You pay the genie $50 at the start, leaving you with a prospect that’s certainly worse than one you could have ended up with, i.e. without paying, and so irrational. This also looks like paying $50 to not find out .
You're forced to act irrationally either way.
Anti-utilitarian theorems
Harsanyi, 1955 proved that our social (or moral or impersonal) preferences over prospects should be to maximize the expected value of a weighted sum of individual utilities in fixed population cases, assuming our social preferences and each individual’s preferences (or betterness) satisfy the standard axioms of expected utility theory and assuming our social preferences satisfy Ex Ante Pareto. Ex Ante Pareto is defined as follows: if between two options, and , everyone is at least as well off ex ante — i.e. is at least as good as for each individual —, then according to our social preferences. Under these assumptions, according to the theorem, each individual in the fixed population has a utility function, , and our social preferences over prospects for each fixed population can be represented by the expected value of a utility function, this function equal to a linear combination of these individual utility functions, . In other words,
if and only if .
Now, if each individual’s utility function in a fixed finite population is bounded, then our social welfare function for that population, from Harsanyi’s theorem, would also be bounded. One might expect the combination of total utilitarianism and Harsanyi’s theorem to support expectational total utilitarianism.[16] However, either the axioms themselves (e.g. the continuity/Archimedean axiom, or general versions of Independence or the Sure-Thing Principle) rule out expectational total utilitarianism, or the kinds of arguments used to defend the axioms (Russell and Isaacs, 2021). For example, essentially the same money pump argument, as we just saw, can be made against it. So, in fact, rather than supporting total utilitarianism, the arguments supporting the axioms of Harsanyi’s theorem refute total utilitarianism.
Perhaps you’re unconvinced by money pump arguments (e.g. Halstead, 2015) or expected utility theory in general. Harsanyi’s theorem has since been generalized in multiple ways. Recent results, without relying on the Independence axiom or Sure-Thing Principle at all, effectively obtain expectational utilitarianism in finite population cases or views including it as a special case, and with some further assumptions, expectational total utilitarianism specifically (McCarthy et al., 2020, sections 4.3 and 5 of Thomas, 2022, Gustafsson et al., 2023). They therefore don’t depend on support from money pump arguments either. In deterministic finite population cases and principles constrained to those cases, arguments based on Separability have also been used to support utilitarianism or otherwise additive social welfare functions (e.g. Theorem 3 of Blackorby et al., 2002 and section 5 of Thomas, 2022). So, there are independent arguments for utilitarianism, other than Harsanyi's original theorem.
However, recent impossibility results undermine them all, too. Given a preorder over prospects[17]:
- Goodsell, 2021 shows Stochastic Dominance, Anteriority and Impartiality are jointly inconsistent. This follows from certain St Petersburg game-like prospects over the population size but constant welfare levels. It also requires an additional weak assumption that most impartial axiologies I’ve come across satisfy[18]: there's some finite population of equal welfare such that adding two more people with the same welfare is either strictly better or strictly worse. For example, if everyone has a hellish life, adding two more people with equally hellish lives should make things worse.
- Russell, 2023 (Theorem 4) shows “Stochastic Dominance, Separability, and Compensation are jointly inconsistent”. As a corollary, Stochastic Dominance, Separability and Impartiality are jointly inconsistent, because Impartiality implies Compensation.
Russell, 2023 has some other impossibility results of interest, but I’ll focus on Theorem 4. I will define and motivate the remaining conditions here. See the papers for the proofs, which are short but technical.
Stochastic Dominance is generally considered to be a requirement of instrumental rationality, and it is a combination of two fairly obvious principles, Stochastic Equivalence and Statewise Dominance (e.g. Tarsney, 2020, Russell, 2023[19]). Stochastic Equivalence requires us to treat two prospects as equivalent if for each set of outcomes, the two prospects are equally likely to have their outcome in that set, and we call such prospects stochastically equivalent. For example, if I win $10 if a coin lands heads, and lose $10 if it lands tails, that should be equivalent to me to winning $10 on tails and losing $10 on heads, with a perfectly 50-50 coin. It shouldn’t matter how the probabilities are arranged, as long as each outcome occurs with the same probability. Statewise Dominance requires us to treat a prospect as at least as good as if is at least as good as with probability 1, and we’d say statewise dominates in that case.[20] It further requires us to treat as strictly better than , if on top of being at least as good as with probability 1, A is strictly better than with some positive probability, and in this case strictly statewise dominates . Informally, statewise dominates if is always at least as good as , and strictly statewise dominates if on top of that, can also be better than .
If instrumental rationality requires anything at all, it’s hard to deny that it requires respecting Stochastic Equivalence and Statewise Dominance. And, you respect Stochastic Dominance if and only if you respect both Stochastic Equivalence and Statewise Dominance, assuming transitivity. We’ll say stochastically dominates if there are prospects and to which and are respectively stochastically equivalent and such that statewise dominates (we can in general take or , but not both), and strictly stochastically dominates if there are such and such that strictly statewise dominates .
Impartiality can be stated in multiple equivalent ways for outcomes (deterministic cases) in finite populations:
- only the distribution of welfares — the number of individuals at each welfare level (or lifetime welfare profiles) — matter in a population matter, not who realizes them or where or when they are realized, or
- we can replace in an individual in any outcome with another individual at the same welfare level (or lifetime welfare profile), and the two outcomes will be equivalent.
Compensation is roughly the principle “that we can always compensate somehow for making things worse nearby, by making things sufficiently better far away (and vice versa)” (Russell, 2023). It is satisfied pretty generally by theories that are impartial in deterministic finite cases, including total utilitarianism, average utilitarianism, variable value theories, prioritarianism, critical-level utilitarianism, egalitarianism and even person-affecting versions of any of these views. In particular, theoretically “moving” everyone to nearby or “moving” everyone to far away without changing their welfare levels suffices.
Anteriority is a weaker version of Ex Ante Pareto: our social preferences are indifferent between two prospects whenever each individual is indifferent. The version Goodsell, 2021 uses, however, is stronger than typical statements of Anteriority and requires its application across different number cases:
If each possible person is equally likely to exist in either of two prospects, and for each welfare level, each person is, conditional on their existence, equally likely to have a life at least that good on either prospect, then those prospects are equally good overall.
This version is satisfied by expectational total utilitarianism, at least when the sizes of the populations in the prospects being compared are bounded by some finite number.
Separability is roughly the condition that parts of the world unaffected in a choice between two prospects can be ignored for ranking those prospects. What’s better or permissible shouldn’t depend on how things went or go for those unaffected by the decision.[21] Or, following Russell, 2023, what we should do that only affects what’s happening nearby (in time and space) shouldn’t depend on what’s happening far away. In particular, in support of Separability and initially raised against average utilitarianism, there’s the Egyptology objection: the study of ancient Egypt and the welfare of ancient Egyptians “cannot be relevant to our decision whether to have children” (Parfit 1984, p. 420).[22]
Separability can be defined as follows: for all prospects , and concerning outcomes for entirely separate things from both and ,
if and only if ,
where means combining or concatenating the prospects. For example, could be the welfare of ancient Egyptians, while and are the welfare of people today; the two may not be statistically independent, but they are separate, concerning disjoint sets of people and welfare levels. Average utilitarianism, many variable value theories and versions of egalitarianism are incompatible with Separability.
Separability is closely related to Anteriority and Ex Ante Pareto. Of course, Harsanyi’s theorem establishes Separability based on Ex Ante Pareto (or Anteriority) and axioms of Expected Utility Theory in fixed finite population cases, but we don’t need all of Expected Utility Theory. Separability, or at least in a subset of cases, follows from Anteriority (or Ex Ante Pareto) and some other modest assumptions, e.g. section 4.3 in Thomas, 2022. On the other hand, a preorder satisfying Separability, and in one-person cases, Anteriority or Ex Ante Pareto, will also satisfy Anteriority or Ex Ante Pareto, respectively, in fixed finite population cases.
So, based on the two theorems, if we assume Stochastic Dominance and Impartiality,[23] then we can’t have Anteriority (unless it’s not worse to add more people to hell) or Separability. Anteriority and Separability are principles used to support utilitarianism, or at least natural generalizations of them defensible by essentially the same arguments. This substantially undermines all arguments for utilitarianism based on these principles. And my impression is that there aren’t really any other good arguments for utilitarianism, but I welcome readers to point any out!
Summary so far
To summarize the arguments so far (given some basic assumptions):
- Unbounded utility functions and expectational total utilitarianism in particular are irrational because of essentially the same arguments as those used to support expected utility theory in the first place, including money pumps.
- All plausible views either give up an even more basic requirement of rationality, Stochastic Dominance, or one of two other principles — or natural extensions that can be motivated the same way — used to defend utilitarianism, i.e. Impartiality or Anteriority.
- All plausible views either give up Stochastic Dominance, or one of two other principles — or natural extensions that can be motivated the same way — used to defend utilitarianism, i.e. Compensation (and so Impartiality) or Separability.
- Together, it seems like the major arguments for utilitarianism in the first place actually undermine utilitarianism.
Responses
Things look pretty bad for unbounded utility functions and utilitarianism. However, there are multiple responses someone might give in order to defend them, and I consider three here:
- We only need to satisfy versions of the principles concerned with prospects with only finitely many outcomes, because infinities are too problematic generally.
- Accept irrational behaviour (at least in some hypotheticals) or deny its irrationality.
- Accept violating foundational principles for utilitarianism in the general cases, but this only somewhat undermines utilitarianism, as other theories may do even worse.
- EDIT to add: The results undermine many other views, not just utilitarianism.
To summarize my opinion on these, I think 1 is a bad argument, but 2, 3 and 4 seem defensible, although 2 and 3 accept that expected utility maximization and utilitarianism are at least somewhat undermined, respectively. On 4, I still think utilitarianism takes the bigger hit, but that doesn't mean it's now less plausible than alternatives. I elaborate below.
Infinities are generally too problematic
First, one might claim the generalizations of axioms of expected utility theory, especially Independence or the Sure-Thing Principle, or even Separability, as well money pumps and Dutch books in general, should count only for prospects over finitely many possible outcomes, given other problems and paradoxes with infinities for decision theory, even expected utility theory with bounded utilities, as discussed in Arntzenius et al., 2004, Peterson, 2016 and Bales, 2021. Expected utility theory with unbounded utilities is consistent with the finitary versions, and some extensions of finitary expected utility theory are also consistent with Stochastic Dominance applied over all prospects, including those with infinitely many possible outcomes (Goodsell, 2023, see also earlier extensions of finitary expected utility to satisfy statewise dominance in Colyvan, 2006, Colyvan, 2008, which can be further extended to satisfy Stochastic Dominance[24]). Stochastic Dominance, Compensation and the finitary version of Separability are also jointly consistent (Russell, 2023). However, I find this argument unpersuasive:
- Plausible and rational decision theories can accommodate infinitely many outcomes, e.g. with bounded utility functions. Not all uses of infinities are problematic for decision theory in general, so the argument from other problems with infinities doesn’t tell us much about these problems. Measure theory and probability theory work fine with these kinds of infinities. The argument proves too much.
- It’s reasonable to consider prospects with infinitely many possible outcomes in practice (e.g. for the “lifetime” of our universe, for sizes of the multiverse, the possibility of continuous spacetime, for the number of moral patients in our multiverse, Russell, 2023), and it’s plausible that all of our prospects have infinitely many possible outcomes, so our decision theory should handle them well. One might claim that we can uniformly bound the number of possible outcomes by a finite number across all prospects. But consider the maximum number across all prospects, and a maximally valuable (or maximally disvaluable) but finite value outcome. We should be able to consider another outcome not among the set. Add a bit more consciousness in a few places, or another universe in the multiverse, or extend the time that can support consciousness a little. So, the space of possibilities is infinite, and it’s reasonable to consider prospects with infinitely many possible outcomes. Furthermore, a probabilistic mixture of any prospect with a heavy-tailed prospect (St Petersburg-like, infinite or undefined expected utility) is heavy-tailed. If you think there's some nonzero chance that it's heavy-tailed, then you should believe now that it's heavy-tailed. If you think there's some nonzero chance that you'd come to believe there's some nonzero chance that it's heavy-tailed, then you should believe now that it's heavy-tailed. You'd need absolute certainty to deny this.
- It’s plausible that if we have an unbounded utility function (or similarly unbounded preferences), we are epistemically required to treat all of our prospects as involving St Petersburg game-like subdistributions, because we can’t justify ruling them out with certainty (see also Cromwell's rule - Wikipedia). It would be objectionably dogmatic to rule them out.
- This doesn’t prevent irrational behaviour in theory. If we refuse to rank St Petersburg-like prospects as strictly preferable to each of their outcomes, we give up statewise (and stochastic) dominance or transitivity (see the previous footnote [11]), each of which is irrational. If we don’t (e.g. following Goodsell, 2023), the same arguments that support the finite versions of Independence and the Sure-Thing Principle can be made against the countable versions (e.g. Russell and Isaacs, 2021, the money pump argument earlier). And the Egyptology objection for Separability generalizes, too (as pointed out in Russell, 2023). If those arguments don’t have (much) force in the general cases, then they shouldn’t have (much) force in the finitary cases, because the arguments are the same.
Accept irrational behaviour or deny its irrationality
A second response is to just bite the bullet and accept apparently irrational behaviour in some (at least hypothetical) circumstances, or deny that it is in fact irrational at all. However, this, too, weakens the strongest arguments for expected utility maximization. The hypothetical situations where irrational decisions would be forced could be unrealistic or very improbable, and so seemingly irrational behaviour in them doesn’t matter, or matters less. The money pump I considered doesn’t seem very realistic, and it’s hard to imagine very realistic versions. Finding out the actual value (or a finite upper bound on it) of a prospect with infinite expected utility conditional on finite actual utility would realistically require an unbounded amount of time and space to even represent. Furthermore, for utility functions that scale relatively continuously with events over space and time, with unbounded time, many of the events contributing utility will have happened, and events that have already happened can’t be traded away. That being said:
- The issues with the money pump argument don't apply to the impossibility theorems for Stochastic Dominance, Impartiality (or Compensation) and Anteriority or Separability. Those are arguments about the right kinds of views to hold. The proofs are finite, and at no point do we need to imagine someone or something with arbitrarily large representations of value (except the outcome being a representation of itself).
- I expect the issue about events already happening to be addressable in principle by just subtracting from B - $100 the value in A already accumulated in the time it took to estimate the actual value of A, assuming this can be done without all of A’s value having already been accumulated.
Still, let's grant that there's something to this, and we don't need to be meet these requirements all of the time or at least in all hypotheticals. Then, other considerations, like Separability, can outweigh them. However, if expectational total utilitarianism is still plausible despite irrational behaviour in unrealistic or very improbable situations, then it seems irrational behaviour in unrealistic or very improbable situations shouldn’t count decisively against other theories or other normative intuitions. So, we open up the possibility to decision theories other than expected utility theory. Furthermore, the line for “unrealistic or very improbable” seems subjective, and if we draw a line to make an exception for utilitarianism, there doesn’t seem to be much reason why we shouldn’t draw more permissive lines to make more exceptions.
Indeed, I don’t think instrumental rationality or avoiding money pumps in all hypothetical cases is normatively required, and I weigh them with my other normative intuitions, e.g. epistemic rationality or justifiability (e.g. Schoenfield, 2012 on imprecise credences). I’d of course prefer to be money pumped or violate Stochastic Dominance less. However, a more general perspective is that foreseeably doing worse by your own lights is regrettable, but regrettable only to the extent of your actual losses from it. There are often more important things to worry about than such losses, like situations of asymmetric information, or just doing better by the lights of your other intuitions. Furthermore, having to abandon another principle or reason you find plausible or otherwise change your views just to be instrumentally rational can be seen as another way of foreseeably doing worse by your own lights. I'd rather hypothetically lose than definitely lose.
Sacrifice or weaken utilitarian principles
A third response is of course to just give up or weaken one or more of the principles used to support utilitarianism. We could approximate expectational total utilitarianism with bounded utility functions or just use stochastic dominance over total utility (Tarsney, 2020), even agreeing in all deterministic finite population cases, and possibly “approximately” satisfying these principles in general. We might claim that moral axiology should only be concerned with betterness per se and deterministic cases. On the other hand, risk and uncertainty are the domains of decision theory, instrumental rationality and practical deliberation, just aimed at ensuring we act consistently with our understanding of betterness. What you have most reason to do is whatever maximizes actual total welfare, regardless of your beliefs about what would achieve this. It’s not a matter of rationality that what you should do shouldn’t depend on things unaffected by your decisions even in uncertain cases or that we should aim to maximize each individual’s expected utility. Nor are these matters of axiology, if axiology is only concerned with deterministic cases. So, Separability and Pareto only need to apply in deterministic cases, and we have results that support total utilitarianism in finite deterministic cases based on them, like Theorem 3 of Blackorby et al., 2002 and section 5 of Thomas, 2022.
That the deterministic and finitary prospect versions of these principles are jointly consistent and support (extensions of) (expectational total) utilitarianism could mean arguments defending these principles provide some support for the view, just less than if the full principles were jointly satisfiable. Other views will tend to violate restricted or weaker versions or do so in worse ways, e.g. not just failing to preserve strict inequalities in Separability but actually reversing them. Beckstead and Thomas, 2023 (footnote 19) point to “the particular dramatic violations [of Separability] to which timidity leads.” If we find the arguments for the principles intuitively compelling, then it’s better, all else equal, for our views to be “more consistent” with them than otherwise, i.e. satisfy weaker or restricted versions, even if not perfectly consistent with the general principles. Other views could still just be worse. Don't let the perfect be the enemy of the good, and don't throw the baby out with the bathwater.
It's not just utilitarianism
EDIT: A final response is to point out that these results undermine much more than just utilitarianism. If we give up Anteriority, then we give up Strong Ex Ante Pareto, and if we give up Strong Ex Ante Pareto, we have much less reason to satisfy its restriction to deterministic cases, Strong Pareto, because similar arguments support both. Strong Pareto seems very basic and obvious: if we can make an individual or multiple individuals better off without making anyone worse off,[25] we should. Having to give up Impartiality or Anteriority, and therefore it seems, Impartiality or Strong Pareto, puts us in a similar situation as infinite ethics, where extensions of Impartiality and Pareto are incompatible in deterministic cases with infinite populations (Askell, 2018, Askell, Wiblin and Harris, 2018). However, in response, I do think there's at least one independent reason to satisfy Strong Pareto but not (Strong) Ex Ante Pareto or Anteriority: extra concern for those who end up worse off (ex post equity) like an (ex post) prioritarian, egalitarian or sufficientarian. Priority for the worse off doesn't give us a positive argument to have a bounded utility function in particular or avoid the sorts of problems here (even if not exactly the same ones). It just counts against some positive arguments to have an unbounded utility function, specifically the ones depending on Anteriority or Ex Ante Pareto. But that still takes away more from what favoured utilitarianism than from what favoured, say, (ex post) prioritarianism. It doesn't necessarily make prioritarianism or other views more plausible than utilitarianism, but utilitarianism takes the bigger hit to its plausibility, because what seemed to favour utilitarianism so much has turned out to not favour it as much as we thought. You might say utilitarianism had much more to lose, i.e. Harsanyi's theorem and generalizations.
Acknowledgements
Thanks to Jeffrey Sanford Russell for substantial feedback on a late draft, as well as Justis Mills and Hayden Wilkinson for helpful feedback on an earlier draft. All errors are my own.
- ^
An individual’s welfare can be the value of their own utility function, although preferences or utility functions defined in terms of each other can lead to contradictions through indirect self-reference (Bergstrom, 1989, Bergstrom, 1999, Vadasz, 2005, Yann, 2005 and Dave and Dodds, 2012). I set aside this issue here.
- ^
This argument works with a step size that's bounded below, even by a tiny value, like 1 millionth of a second or 1 millionth more (counterfactual) utility. If the step sizes have to keep getting smaller and smaller and converge to 0, then we may never reach .
- ^
Although there are stronger arguments that's actually infinite. It's one of the simplest and most natural models that fits with our observations of global flatness. See the Wikipedia article Shape of the Universe.
- ^
For generalizations without actual utility values, see violations of Limitedness in Russell and Isaacs, 2021 and reckless preferences in Beckstead and Thomas, 2023.
- ^
Independence: For any prospects , and , and probability , if , then ,
where is the prospect that's with probability , and with probability .
Russell and Isaacs, 2021 define Countable Independence as follows:
For any prospects , and , and any probabilities that sum to one, if , then
If furthermore for some such that , then
The standard finitary Independence axiom is a special case.
- ^
The Sure Thing Principle can be defined as follows:
Let and be prospects, and let be some event with probability neither 0 nor 1. If conditional on each of and , then . If furthermore, conditional on or A < B conditional on , then .
In other words, if we weakly prefer either way, then we should just weakly prefer . And if, furthermore, we strictly prefer on one of the two possibilities, then we should just strictly prefer .
Russell and Isaacs, 2021 define the Countable Sure Thing Principle as follows:
Let and be prospects, and let be a (countable) set of mutually exclusive and exhaustive events, each with non-zero probability. If conditional on each , then . If furthermore, conditional on some , then .
- ^
See also Christiano, 2022. Both depend on St Petersburg game-like prospects with infinitely many possible outcomes and, when defined, infinite expected utility. For more on the St Petersburg paradox, see Peterson, 2023. Some other foreseeable sure loss arguments require a finite but possibly unbounded number of choices, like McGee, 1999 and Pruss, 2022.
- ^
Or, as in Russell and Isaacs, 2021, each of the countably many prospects used to construct it.
- ^
Note that the probabilities sum to 1, because , so this is in fact a proper probability distribution.
The expected value is
- ^
From for each , we have, by induction, . Then, for each ,
,
which can be arbitrarily large, so .
- ^
This would follow either by extension to expected utilities over countable prospects, or assuming we respect Statewise Dominance and transitivity.
For the latter, we can modify the prospect to a truncated one with finitely many outcomes for each , by defining if , and (or ) otherwise. Then is finite for each N, but . Furthermore, for each N, not only is it the case that , but also strictly statewise dominates , i.e. X is with certainty at least as good as , and is, with nonzero probability, strictly better. So, given any prospect with finite (expected) utility, there’s an such that , so , but since , by transitivity, .
- ^
For Countable Independence: We defined . We can let in the definition of Countable Independence. However, it's also the case that , so we can let in the definition of Countable Independence. But for each , so by Countable Independence, , contrary to reflexivity.
For the Countable Sure-Thing Principle: define to be identically distributed to but independent from . Let . for each , so conditional on , for each . By the Countable Sure-Thing Principle, this would imply . However, doing the same with also gives us , violating transitivity.
These arguments extend to the more general kinds of improper prospects in Russell and Isaacs, 2021.
- ^
In practice, you should give weight to the possibility that it has infinite or undefined value. However, the argument that follows can be generalized to this case using stochastic dominance reasoning or, if you do break ties between actual infinities, any reasonable way of doing so.
- ^
Or give you an accurate finite upper bound on how it will turn out.
- ^
And the genie isn’t going to do anything good with it.
- ^
Interestingly, if expectational total utilitarianism is consistent with Harsanyi’s theorem, then it is not the only way for total utilitarianism to be consistent with Harsanyith’s theorem. Say individual welfare takes values in the interval . Then the utility functions and agree with both Harsanyi’s theorem and total utilitarianism. According to them, a larger population is always better than a smaller population, regardless of the welfare levels in each. However, some further modest assumptions give us expectational total utilitarianism, e.g. each individual can welfare level 0.
- ^
So, assuming reflexivity, transitivity, the Independence of Irrelevant Alternatives. Also, we need the set of prospects to be rich enough to include some of the kinds of prospects used in the proofs.
- ^
Exceptions include average utilitarianism, symmetric person-affecting views, maximin and maximax.
- ^
Russell, 2023 writes:
Stochastic Dominance is a fairly uncontroversial principle of decision theory—even among those who reject other parts of standard expectational decision theory (such as Quiggin, 1993; Broome, 2004), and even in settings where other parts of standard expectational decision theory give out (see for example Easwaran, 2014).10 We should not utterly foreclose giving up Stochastic Dominance—we are facing paradoxes, so some plausible principles will have to go—but I do not think this is a very promising direction. In what follows, I will take Stochastic Dominance for granted.
and in footnote 10:
For other defenses of Stochastic Dominance, on which I here have drawn, see Tarsney (2020, 8); Wilkinson (2022, 10); Bader (2018).
- ^
There is some controversy here, because we might instead say that A statewise dominates if and only if is at least as good as under every possibility, including each possibility with probability 0. Russell, 2023 writes:
For example, the probability of an ideally sharp dart hitting a particular point may be zero—but the prospect of sparing a child from malaria if the dart hits that point (and otherwise nothing) may still be better than the prospect of getting nothing no matter what. But these two prospects are stochastically equivalent. Perhaps what is best depends on what features of its outcomes are sure—where in general this can come apart from what is almost sure—that is, has probability one.
However, I don’t think this undermines the results of Russell, 2023, because the prospects considered don’t disagree on any outcomes of probability 0.
- ^
Insofar as it isn’t evidence for how well off moral patients today and in the future can or will be, and ignoring acausal influence.
- ^
The same objection is raised earlier in McMahan, 1981, p. 115 referring to past generations more generally. See also discussion of it and similar objections in Huemer, 2008, Wilkinson, 2022, Beckstead and Thomas, 2023, Wilkinson, 2023 and Russell, 2023.
- ^
And a single preorder over prospects, so transitivity, reflexivity and the independence of irrelevant alternatives, and a rich enough set of possible prospects.
- ^
These can be extended to satisfy Stochastic Dominance by making stochastically equivalent prospects equivalent and taking the transitive closure to get a new preorder.
- ^
Or, while keeping everyone at least as well off, in cases of incomparability.

I'd be happy to get constructive criticism, given downvotes I was getting soon after posting. I'll leave some comment replies here for people to agreevote/disagreevote with in case they want to stay anonymous. I also welcome feedback as comments here or private messages.
I've removed my own upvotes from these comments so this thread doesn't start at the top of the comment section. EDIT: Also, keep my comments in this thread at 0 karma if you want to avoid affecting my karma for making so many comments.
I haven't downvoted it, and I'm sorry you're getting that response for a thoughtful and in-depth piece of work, but I can offer a couple of criticisms I had that have stopped me upvoting it yet because I don't feel like I understand it, mixed in with a couple of criticisms where I feel like I did:
Thanks for the feedback and criticism!
Hmm, I didn't expect or intend for people to dig through the links, but it looks like I misjudged what things people would find cruxy for the rest of the arguments but not defended well enough, e.g. your concerns with infinite expected utility.
EDIT: I've rewritten the arguments for possibly unbounded impacts.
But can you produce a finite upper bound on our lightcone that you're 100% confident nothing can pass? (It doesn't have to be tight.) If not, then you could consider a St Petersburg-like prospect, with for each n, has probability 1/2n of size (or impact) 2n, in whatever units you're using. That's finite under every possible outcome, but it has an infinite expected value.
Section II from Carlsmith, 2021 is one of the best arguments for acausal influence I'm aware of, in case you're interested in something more convincing. (FWIW, I also thought acausal influence was crazy for a long time, and I didn't find Newcomb's problem to be a compelling reason to reject causal decision theory.)
EDIT: I've now cut the acausal stuff and just focus on unbounded duration.
This follows from the theorems I cited, but I didn't include proofs of the theorems here. The proofs are technical and tricky,[1] and I didn't want to make my post much longer or spend so much more time on it. Explaining each proof in an intuitive way could probably be a post on its own.
How long you live could be distributed like a St Petersburg gamble, e.g. for each n, with probability 1/2n., you could live 2n years. The expected value of that is infinite, even though you'd definitely only live a finite amount of time.
Ya, I got similar feedback on an earlier draft for making it harder to read, and tried to cut some uses of the word, but still left a bunch. I'll see if I can cut some more.
They work by producing some weird set of prospects. They then show that you can't order them in a way that satisfies the axioms, applying them one-by-one and then violating one of them or getting a contradiction.
I think Vasco already made this point elsewhere, but I don't see why you need certainty about any specific line to have finite expectation. If for the counterfactual payoff x, you think (perhaps after a certain point) xP(x) approaches 0 as x tends to infinity, it seems like you get finite expectation without ever having absolute confidence in any boundary (this applies to life expectancy, too).
Thanks! I had a look, and it still doesn't persuade me, for much the reasons Newcomb's problem didn't. In roughly ascending importance
I would be less interested to see a reconstruction of a proof of the theorems and more interested to see them stated formally and a proof of the claim that it follows from them.
On Carlsmith's example, we can just make it a logical necessity by assuming more. And, as you acknowledge the possibility, some distinctions can be too fine. Maybe you're only 5% sure your copy exists at all and the conditions are right for you to get $1 million from your copy sending it.
5%*$1 million = $50,000 > $1,000, so you still make more in expectation from sending a million dollars. You break even in expected money if your decision to send $1 million increases your copy's probability of sending $1 million by 1/1,000.
I do find it confusing to think about decision-making under determinism, but I think 3 proves too much. I don't think quantum indeterminacy or randomness saves free will or agency if it weren't already saved, and we don't seem to have any other options, assuming physicalism and our current understanding of physics.
Ya, I agree you don't need certainty about the bound, but now you need certainty about the distribution not being heavy-tailed at all. Suppose your best guess is that it looks like some distribution X, with finite expected value. Now, I suggest that it might actually be Y, which is heavy-tailed (has infinite expected value). If you assign any nonzero probability to that being right, e.g. switch to pY+(1−p)X for some p>0, then your new distribution is heavy-tailed, too. In general, if you think there's some chance you'd come to believe it's heavy-tailed, then you should believe now that it's heavy-tailed, because a probabilistic mixture with a heavy-tailed distribution is heavy-tailed. Or, if you think there's some chance you'd come to believe there's some chance it's heavy-tailed, then you should believe now that it's heavy-tailed.
(Vasco's claim was stronger: the difference is exactly 0 past some point.)
Hmm, I might be misunderstanding.
I already have formal statements of the theorems in the post:
All of those terms are defined in the section Anti-utilitarian theorems. I guess I defined Impartiality a bit informally and might have hidden some background assumptions (preorder, so reflexivity + transitivity, and the set of prospects is every probability distribution over outcomes in the set of outcomes), but the rest were formally defined.
Then, from 1, assuming Stochastic Dominance and Impartiality, Anteriority must be false. From 2, assuming Stochastic Dominance and Impartiality, Separability must be false. Therefore assuming Stochastic Dominance and Impartiality, Anteriority and Separability must both be false.
The post is too long.
The title is bad, e.g. too provocative, clickbaity, overstates the claims or singles out utilitarianism too much (there are serious problems with other views).
EDIT: I've changed the title to "Arguments for utilitarianism are impossibility arguments under unbounded prospects". Previously, it was "Utilitarianism is irrational or self-undermining". Kind of long now, but descriptive and less provocative.
I've changed the title to "Arguments for utilitarianism are impossibility arguments under unbounded prospects". Previously, it was "Utilitarianism is irrational or self-undermining". Kind of long now, but descriptive and less provocative.
My response: I admit it's provocative and sounds like clickbait, but it literally describes what I'm arguing. Maybe I should water it down, e.g. "Utilitarianism seems irrational or self-undermining" or "Utilitarianism is plausibly irrational or self-undermining"? I guess someone could reject all of the assumed requirements of rationality used here. I'm personally sympathetic to that myself (although Stochastic Dominance seems pretty hard to give up, but I think difference-making risk aversion is a plausible reason to give it up), so maybe the title even makes a claim stronger than what I'm confident in.
It's still a claim that seems plausible enough to me to state outright as-is, though. (EDIT: I also don't think the self-undermining bit should be controversial, but how much it would self-undermine is a matter of degree and subjective. Maybe "self-undermine" isn't the right word, because that suggests that utilitarianism is false, not just that we've weakened positive arguments for utilitarianism).
Also, maybe it is unfair to single out utilitarianism in particular.
Recommendation: A collection of paradoxes dealing with Utilitarianism. This seems to me to be what you wrote, and would have had me come to the post with more of a “ooo! Fun philosophy discussion” rather than “well, thats a very strong claim… oh look at that, all so called inconsistencies and irrationalities either deal with weird infinite ethics stuff or are things I can’t understand. Time to be annoyed about how the headline is poorly argued for.” the latter experience is not useful or fun, the former nice depending on the day & company.
Thanks for the feedback!
I think your general point can still stand, but I do want to point out that the results here don't depend on actual infinities (infinite universe, infinitely long lives, infinite value), which is the domain of infinite ethics. We only need infinitely many possible outcomes and unbounded but finite value. My impression is that this is a less exotic/controversial domain (although I think an infinite universe shouldn't be controversial, and I'd guess our universe is infinite with probability >80%).
Furthermore, impossibility results in infinite ethics are problematic for everyone with impartial intuitions, but the results here seem more problematic for utilitarianism in particular. You can keep Impartiality and Pareto and/or Separability in deterministic + unbounded but finite cases here, but when extending to uncertain cases, you wouldn't end up with utilitarianism, or you'd undermine utilitarianism in doing so. You can't extend both Impartiality and Pareto to infinite cases (allowing arbitrary bijections or swapping infinitely many people in Impartiality), and this is a problem for everyone sympathetic to both principles, not just utilitarians.
This seems pretty important to me. You can handwave away standard infinite ethics by positing that everything is finite with 100% certainty, but you can't handwave away the implications of a finite-everywere distribution with infinite EV.
(Just an offhand thought, I wonder if there's a way to fix infinite-EV distributions by positing that utility is bounded, but that you don't know what the bound is? My subjective belief is something like, utility is bounded, I don't know the bound, and the expected value of the upper bound is infinity. If the upper bound is guaranteed finite but with an infinite EV, does that still cause problems?)
I think someone could hand-wave away heavy tailed distributions, too, but rather than assigning some outcomes 0 probability or refusing to rank them, they're assuming some prospects of valid outcomes aren't valid or never occur, even though they're perfectly valid measure-theoretically. Or, they might actually just assign 0 probability to outcomes outside those with a bounded range of utility. In the latter case, you could represent them with both a bounded utility function and an unbounded utility function, agreeing on the bounded utility set of outcomes.
You could have moral/normative uncertainty across multiple bounded utility functions. Just make sure you don't weigh them together via maximizing expected choiceworthiness in such a way that the weighted sum of utility functions is unbounded, because the weighted sum is a utility function. If the weighted sum is unbounded, then the same arguments in the post will apply to it. You could normalize all the utility functions first. Or, use a completely different approach to normative uncertainty, e.g. a moral parliament. That being said, the other approaches to normative uncertainty also violate Independence and can be money pumped, AFAIK.
Fairly related to this is section 6 in Beckstead and Thomas, 2022. https://onlinelibrary.wiley.com/doi/full/10.1111/nous.12462
Hmm, in response, one might claim that if we accept Pareto (in deterministic finite cases), we should accept Ex Ante Pareto + Anteriority (including Goodsell's version), too, and if we accept Separability in deterministic finite cases, we should accept it in uncertain and possibly unbounded but finite cases, too. This would be because the arguments for the stronger principles are similar to the arguments for the weaker more restricted setting ones. So, there would be little reason to satisfy Pareto and Separability only in bounded and/or deterministic cases.
Impartiality + (Ex Ante Pareto or Separability) doesn't work in unbounded but finite uncertain cases, but because of this, we should also doubt Impartiality + (Pareto or Separability) in unbounded but finite deterministic cases. And that counts against a lot more than just utilitarianism.
Personally, I would have kept the original title. Titles that are both accurate and clickbaity are the best kind - they get engagement without being deceptive.
I don't think karma is always a great marker of a post's quality or appropriateness. See an earlier exchange we had.
Unfortunately, I think clickbait also gets downvotes even if accurate, and that will drop the post down the front page or off it.
I might have gone for "Utilitarianism may be irrational or self-undermining" rather than "Utilitarianism is irrational or self-undermining".
The post is misleading, because it singles out utilitarianism too much without pointing out serious problems with other views.
This post isn't useful.
As a special case: these kinds of results have already been discussed enough in the community.
My writing is unclear. Some things could have been better explained or explained in more detail (I got similar feedback on LW here). Or, my sentence structure is bad/hard to follow.
I think this subject is very important and underrated, so I'm glad you wrote the post, and you raised some points that I wasn't aware of, and I would like to see people write more posts like this one. The post didn't do as much for me as it could have because I found two of its three main arguments hard to understand:
Thanks, this is helpful!
To respond to the points:
Some of the (main) arguments are wrong/bad, or the main title claim is wrong.
EDIT: I've changed the title to "Arguments for utilitarianism are impossibility arguments under unbounded prospects". Previously, it was "Utilitarianism is irrational or self-undermining". Kind of long now, but descriptive and less provocative.
Thanks for the post, Michael! I strongly endorse expectational total hedonistic utilitarianism, but strongly upvoted it for thoughtfully challenging the status-quo, and because one should be nice to other value systems.
I agree total welfare may be unbounded for the reasons you mention, but I would say differences in total welfare between prospects have to be bounded. I think we have perfect evidential symmetry (simple cluelessness) between prospects beyond a sufficiently large (positive or negative) welfare, in which case the difference between their welfare probability density functions is exactly 0. So I believe the tails of the differences in total welfare between prospects are bounded, and so are the expected differences in total welfare between prospects. One does not know the exact points the tails of the differences in total welfare between prospects reach 0, but that only implies decisions will fall short of perfect, not that what one should do is undefined, right?
I am glad you focussed on real outcomes.
I would reply to this as follows. If "the maximum number across all prospects" is well chosen, one will have perfect evidential symmetry between any prospects for higher welfare levels than the maximum. Consequently, there will be no difference between the prospects for outcomes beyond the maximum, and the expected difference between prospects will be maintained when we "add a bit more consciousness".
Thanks for engaging!
On symmetry between options in the tails, if you think there's no upper bound with certainty on how long our descendants could last, then reducing extinction risk could have unbounded effects. Maybe other x-risks, too. I do think heavy tails like this are very unlikely, but it's hard to justifiably rule them out with certainty.
Or, you could have a heavy tail on the number of non-solipsist simulations, or the number of universes in our multiverse (if spatially very large, or the number of quantum branches, or the number of pocket universes, or if the universe will start over many times, like a Big Bounce, etc.), and acausal influence over what happens in them.
The money pump argument is interesting, but it feels strange to take away a decision-theoretic conclusion from it because the issue seems centrally epistemic. You know that the genie will give you evidence that will lead you to come to believe B has a higher expected value than A. Despite knowing this, you're not willing to change your mind about A and B without that evidence. This is a failure of van Fraassen's principle of reflection, and it's weird even setting any choices you need to make aside. That failure of reflection is what is driving the money pump. Giving up on unbounded utilities or expected value maximization won't save you from the reflection failure, so it seems like the wrong solution. Either there is a purely epistemic solution that will save you or your practical irrationality is merely the proper response to an inescapable epistemic irrationality.
There's also a reflection argument in Wilkinson, 2022, in his Indology Objection. Russell, 2023 generalizes the argument with a theorem:
and Russell, 2023 defines Negative Reflection based on Wilkinson, 2022's more informal argument as follows:
Background Independence is a weaker version of Separability. I think someone who denies Separability doesn't have much reason to satisfy Background Independence, because I expect intuitive arguments for Background Independence (like the Egyptology objection) to generalize to arguments for Separability.
But still, either way, Russell, 2023 proves the following:
This rules out expected utility maximization with unbounded utility functions.
Satisfying the Countable Sure-Thing Principle (CSTP, which sounds a lot like the principle of reflection) and updating your credences about outcomes properly as a Bayesian and looking ahead as necessary should save you here. Expected utility maximization with a bounded utility function satisfies the CSTP so it should be safe. See Russell and Isaacs, 2021 for the definition of the CSTP and a theorem, but it should be quick to check that expected utility maximization with a bounded utility function satisfies the CSTP.
You can also preserve any preorder over outcomes from an unbounded real-valued utility function with a bounded utility function (e.g. apply arctan) and avoid these problems. So to me it does seem to be a problem with the attitudes towards risk involved with unbounded utility functions, and it seems appropriate to consider implications for decision theory.
Maybe it is also an epistemic issue, too, though. Like it means having somehow (dynamically?) inconsistent or epistemically irrational joint beliefs.
Are there other violations of the principle of reflection that aren't avoidable? I'm not familiar with it.
The case reminded me of one you get without countable additivity. Suppose you have two integers drawn with a fair chancy process that is as likely to result in any integer. What’s the probability the second is greater than the first? 50 50. Now what if you find out the first is 2? Or 2 trillion? Or any finite number? You should then think the second is greater.
Ya, that is similar, but I think the implications are very different.
The uniform measure over the integers can't be normalized to a probability distribution with total measure 1. So it isn’t a real (or proper) probability distribution. Your options are, assuming you want to address the problem:
2 gives up a lot more than 1, and there’s no total order we can replace it with that will avoid the problem. Giving up the order also means giving up arithmetical statements about the outcomes of the distribution, because the order is definable from addition or the successor function.
If you give up the total order entirely (not just for the distribution or distributions in general), then you can't even form the standard set of natural numbers, because the total order is definable from addition or the successor function. So, you're forced to give up 1 (and the Axiom of Infinity from ZF) along with it, anyway. You also lose lots of proofs in measure theory.
OTOH, the distribution of outcomes in a St Petersburg prospect isn't improper. The probabilities sum to 1. It's the combination with your preferences and attitudes to risk that generate the problem. Still, you can respond nearly the same two ways:
However, 2 seems to give up less than 1 here, because:
The other unlisted option (here) is that we just accept that infinities are weird and can generate counter-intuitive results and that we shouldn't take too much from them because it is easier to blame them then all of the other things wrapped up with them. I think the ordering on integers is weird, but it's not a metaphysical problem. The weird fact is that every integer is unusually small. But that's just a fact, not a problem to solve.
Infinities generate paradoxes. There are plenty of examples. In decision theory, there is also stuff like Satan's apple and the expanding sphere of suffering / pleasure. Blaming them all on the weirdness of infinities just seems tidier than coming up with separate ad hoc resolutions.
I think there's something to this. I argue in Sacrifice or weaken utilitarian principles that it's better to satisfy the principles you find intuitive more than less (i.e. satisfy weaker versions, which could include the finitary or deterministic case versions, or approximate versions). So, it's kind of a matter of degree. Still, I think we should have some nuance about infinities rather than treat them all the same and paint their consequences as all easily dismissable. (I gather that this is compatible with your responses so far.)
In general, I take actual infinities (infinities in outcomes or infinitely many decisions or options) as more problematic for basically everyone (although perhaps with additional problems for those with impartial
aggregativeviews) and so their problems easier to dismiss and blame on infinities. Problems from probability distributions with infinitely many outcomes seem to apply much more narrowly and so harder to dismiss or blame on infinities.(The rest of this comment goes through examples.)
And I don't think the resolutions are in general ad hoc. Arguments for the Sure-Thing Principle are arguments for bounded utility (well, something more general), and we can characterize the ways that avoid the problem as such (given other EUT axioms, e.g. Russell and Isaacs, 2021). Dutch book arguments for probabilism are arguments that your credences should satisfy certain properties not satisfied by improper distributions. And improper distributions are poorly behaved in other ways that make them implausible for use as credences. For example, how do you define expectations, medians and other quantiles over them — or even the expected value of a nonzero constant functions or two-valued step function over improper distributions — in a way that makes sense? Improper distributions just do very little of what credences are supposed to do.
There are also representation theorems in infinite ethics, specifically giving discounting and limit functions under some conditions in Asheim, 2010 (discussed in West, 2015), and average utilitarianism under others in Pivato (2021, and further discussed in 2022 and 2023).
Satan's apple would be a problem for basically everyone, and it results from an actual infinity, i.e. infinitely many actual decisions made. (I think how you should handle it in practice is to precommit to taking at most a specific finite number of pieces of the apple, or use a probability distribution, possibly one with infinite expected value but finite with certainty.)
Similarly, when you have infinitely many options to choose from, there may not be any undominated option. As long as you respect statewise dominance and have two outcomes A and B, with one strictly worse than the other, then there's no undominated option among the set pA + (1-p)B, for all p strictly between 0 and 1 (with p=1/n or 1-1/n for each n). These are cases where the argument for dismissal is strong, because "solving" these problems would mean giving up the most basic requirements of our theories. (And this fits well with scalar utilitarianism.)
My inclination for the expanding sphere of suffering/pleasure is that there are principled solutions:
I think Parfit's Hitchhiker poses a similar problem for everyone, though.
You're outside town and hitchhiking with your debit card but no cash, and a driver offers to drive you if you pay him when you get to town. The driver can also tell if you'll pay (he's good at reading people), and will refuse to drive if he predicts that you won't. Assuming you'd rather keep your money than pay conditional on getting into town, it would be irrational to pay then (you wouldn't be following your own preferences). So, you predict that you won't pay. And then the driver refuses to drive you, and you lose.
So, the thing to do here is to somehow commit to paying and actually pay, despite it violating your later preference to not pay when you get into town.
And we might respond the same way for A vs B-$100 in the money pump in the post: just commit to sticking with A (at least for high enough value outcomes) and actually do it, even though you know you'll regret it when you find out the value of A.
So maybe (some) money pump arguments prove too much? Still, it seems better to avoid having these dilemmas when you can, and unbounded utility functions face more of them.
On the other hand, you can change your preferences so that you actually prefer to pay when you get into town. Doing the same for the post's money pump would mean actually not preferring B-$100 over some finite outcome of A. If you do this in response to all possible money pumps, you'll end up with a bounded utility function (possibly lexicographic, possibly multi-utility representation). Or, this could be extremely situation-specific preferences. You don't have to prefer to pay drivers all the time, just in Parfit's Hitchhiker situations. In general, you can just have preferences specific to every decision situation to avoid money pumps. This violates the Independence of Irrelevant Alternatives, at least in spirit.
See also https://www.lesswrong.com/tag/parfits-hitchhiker
This seems impossible, for the possibilities that account for ~all the expected utility (without which it's finite)? You can't fit enough bits in a human brain or lifetime (or all accessible galaxies, or whatever). Your brain would have to be expanded infinitely (any finite size wouldn't be enough). And if we're giving you an actually infinite brain, the part about how infinite expectations of finite outcomes are more conservative arguments than actual infinities goes away.
My post also covers two impossibility theorems that don't depend on anyone having arbitrary precision or unbounded or infinite representations of anything:[1]
The proofs are also of course finite, and the prospects used have finite representations, even though they represent infinitely many possible outcomes and unbounded populations.
The actual outcome would be an unbounded (across outcomes) representation of itself, but that doesn't undermine the argument.
I personally think unbounded utility functions don't work, I'm not claiming otherwise here, the comment above is about the thought experiment.
It wouldn't have to definitely be infinite, but I'd guess it would have to be expandable to arbitrarily large finite sizes, with the size depending on the outcome to represent, which I think is also very unrealistic. I discuss this briefly in my Responses section. Maybe not impossible if we're dealing with arbitrarily long lives, because we could keep expanding over time, although there could be other practical physical limits on this that would make this impossible, maybe requiring so much density that it would collapse into a black hole?
One way to illustrate this point is with Turing machines,[1] with finite but arbitrarily expandable tape to write on for memory. There are (finite) Turing machines that can handle arbitrarily large finite inputs, e.g. doing arithmetic with or comparing two arbitrarily large but finite integers. They only use a finite amount of tape at a time, so we can just feed more and more tape for larger and larger numbers. So, never actually infinite, but arbitrarily large and arbitrarily expandable. A similar argument might apply for more standard computer architectures, with expandable memory, but I'm not that familiar with how standard computers work.
You might respond that we need an actual infinite amount of possible tape (memory space) to be able to do this. Like there has to be an infinite amount of matter available to us to turn into memory space. That isn't true. The universe and amount of available matter for tape could be arbitrarily large but finite, and we could (in principle) need less tape than what could be available in all possible outcomes, and the amount of tape we'd need will scale with the "size" or value of the outcome. For example, if we want to represent how long you'll live in years or an upper bound for it, in case you might live arbitrarily long, the amount of tape you'd need would scale with how long you'd live. It could scale much slower, e.g. we could represent the log of the number of years, or the log of the log, or the log of the log of the log, etc.. Still, the length of the tape would have to be unbounded across outcomes.
So, I'd have concerns about:
So the scenario seems unrealistic and physically impossible. But if it's impossible, it's for reasons that don't have to do with infinite value or infinitely large things (although black holes might involve infinities).
For anyone unaware, it's a type of computer that you can actually build and run, but not the architecture we actually use.
This is what I was thinking about. If I need a supply of matter set aside in advance to be able to record/receive an answer, no finite supply suffices. Only an infinite brain/tape, or infinite pile of tape making resources, would suffice.
If the resources are created on demand ex nihilo, and in such a way that the expansion processes can't be just 'left on' you could try to jury rig around it.
The resources wouldn't necessarily need to be created on demand ex nihilo either (although that would suffice), but either way, we're forced into extremely remote possibilities — denying our current best understanding of physics — and perhaps less likely than infinite accessible resources (or other relevant infinities). That should be enough to say it's less conservative than actual infinities and make your point for this particular money pump, but it again doesn't necessarily depend on actual infinities. However, some people actually assign 0 probability to infinity (I think they're wrong to do so), and some of them may be willing to grant this possibility instead. For them, it would actually be more conservative.
The resources could just already exist by assumption in large enough quantities by outcome in the prospect (at least with nonzero probability for arbitrarily large finite quantities). For example, the prospect could be partially about how much information we can represent to ourselves (or recognize). We could be uncertain about how much matter would be accessible and how much we could do with it. So, we can have uncertainty about this and may not be able to put an absolute hard upper bound on it with certainty, even if we could with near-certainty, given our understanding of physics and the universe, and our confidence in them. And this could still be the case conditional on no infinities. So, we could consider prospects with extremely low probability heavy tails for how much we could represent to ourselves, which would have the important features of St Petersburg prospects for the money pump argument. It’s also something we'd care about naturally, because larger possible representations would tend to coincide with much more possible value.
St Petersburg prospects already depend on extremely remote possibilities to be compelling, so if you object to extremely low probabilities or instead assign 0 probability to them (deny the hypothetical), then you can already object at this point without actual infinities. That being said, someone could hold that finding out the value of a St Petersburg prospect to unbounded values is with certainty impossible (without an actual infinity, and so reject Cromwell's rule), but that St Petersburg prospects are still possible despite this.
If you don't deny with certainty the possibility of finding out unbounded values without actual infinities, then, we can allow "Find out A" to fail sometimes, but work in enough exotic possibilities with heavy tails that A conditional on it working (but not its specific value) still has infinite expected utility. Then we can replace B−$100 in the money pump with a prospect D defined as follows in my next comment, and you still get a working money pump argument.
Let C be identically distributed to but statistically independent from A| you'll know A (not any specific value of A). C and A| you'll know A can each have infinite expected utility, by assumption, using an extended definition of "you" in which you get to expand arbitrarily, in extremely remote possibilities. C−$100 is also strictly stochastically dominated by A| you'll know A, so C−$100≺A| you'll know A.
Now, consider the following prospect:
With probability p=P[ you'll know A], it's C−$100. With the other probability 1−p, it'sA| you'll know A. We can abuse notation to write this in short-hand as
D=p(C−$100)+(1−p)(A|you won't know A)=p(C−$100)+(1−p)XThen, letting X=A| you'll know A, we can compare D to
A=p(A| you'll know A)+(1−p)(A|you won't know A)=p(A| you'll know A)+(1−p)XA strictly stochastically dominates D, so D≺A. Then the rest of the money pump argument follows, replacing B−$100 with D, and assuming "Find out A" only works sometimes, but enough of the time that A| you'll know A still has infinite expected utility.[1] You don't know ahead of time when "Find out A" will work, but when it does, you'll switch to D, which would then be C−$100, and when "Find out A" doesn't work, it makes no difference. So, your options become:
Or otherwise beats each of its actual possible outcomes.
On the other hand, if we can't rule out arbitrarily large finite brains with certainty, then the requirements of rationality (whatever they are) should still apply when we condition on it being possible.
Maybe we should discount some very low probabilities (or probability differences) to 0 (and I'm very sympathetic to this), but that would also be vulnerable to money pump arguments and undermine expected utility theory, because it also violates the standard finitary versions of the Independence axiom and Sure-Thing Principle.
I would guess that arbitrarily large but finite (extended) brains are much less realistic than infinite universes, though. I'd put a probability <1% on arbitrarily large brains being possible, but probability >80% on the universe being infinite. So, maybe actual infinities can make do with more conservative assumptions than the particular money pump argument in my post (but not necessarily unboundedness in general).
From my Responses section:
(Maybe I'm understating how unrealistic this is.)
For more on problems for impartiality, including involving infinite populations, and a comparison of some different utilitarian-ish views and how well-behaved they are (especially 45:40 for a table summary), see
https://globalprioritiesinstitute.org/parfit-memorial-lecture-jeffrey-sanford-russell-problems-for-impartiality/
Handout here.
Hi Michael, thanks for the post! I was really happy to see something like this on the EA Forum. In my view, EAs* significantly overestimate the plausibility of total welfarist consequentialism**, in part due to a lack of familiarity with the recent literature in moral philosophy. So I think posts like this are important and helpful.
* I mean this as a generic term (natural language plurals (usually) aren't universally quantified).
** This isn't to suggest that I think there's some other moral theory that is very plausible. They're all implausible, as far as I can tell; which is partly why I lean towards anti-realism in meta-ethics.