Gregory Lewis
Bio
Mostly bio, occasionally forecasting/epistemics, sometimes stats/medicine, too often invective.
Posts 20
Comments297
Hello Michael,
Thanks for your reply. In turn:
1:
HLI has, in fact, put a lot of weight on the d = 1.72 Strongminds RCT. As table 2 shows, you give a weight of 13% to it - joint highest out of the 5 pieces of direct evidence. As there are ~45 studies in the meta-analytic results, this means this RCT is being given equal or (substantially) greater weight than any other study you include. For similar reasons, the Strongminds phase 2 trial is accorded the third highest weight out of all studies in the analysis.
HLI's analysis explains the rationale behind the weighting of "using an appraisal of its risk of bias and relevance to StrongMinds’ present core programme". Yet table 1A notes the quality of the 2020 RCT is 'unknown' - presumably because Strongminds has "only given the results and some supporting details of the RCT". I don't think it can be reasonable to assign the highest weight to an (as far as I can tell) unpublished, not-peer reviewed, unregistered study conducted by Strongminds on its own effectiveness reporting an astonishing effect size - before it has even been read in full. It should be dramatically downweighted or wholly discounted until then, rather than included at face value with a promise HLI will followup later.
Risk of bias in this field in general is massive: effect sizes commonly melt with improving study quality. Assigning ~40% of a weighted average of effect size to a collection of 5 studies, 4 [actually 3, more later] of which are (marked) outliers in effect effect, of which 2 are conducted by the charity is unreasonable. This can be dramatically demonstrated from HLI's own data:
One thing I didn't notice last time I looked is HLI did code variables on study quality for the included studies, although none of them seem to be used for any of the published analysis. I have some good news, and some very bad news.
The good news is the first such variable I looked at, ActiveControl, is a significant predictor of greater effect size. Studies with better controls report greater effects (roughly 0.6 versus 0.3). This effect is significant (p = 0.03) although small (10% of the variance) and difficult - at least for me - to explain: I would usually expect worse controls to widen the gap between it and the intervention group, not narrow it. In any case, this marker of study quality definitely does not explain away HLI's findings.
The second variable I looked at was 'UnpubOr(pre?)reg'.[1] As far as I can tell, coding 1 means something like 'the study was publicly registered' and 0 means it wasn't (I'm guessing 0.5 means something intermediate like retrospective registration or similar) - in any case, this variable correlates extremely closely (>0.95) to my own coding of whether a study mentions being registered or not after reviewing all of them myself. If so, using it as a moderator makes devastating reading:[2]
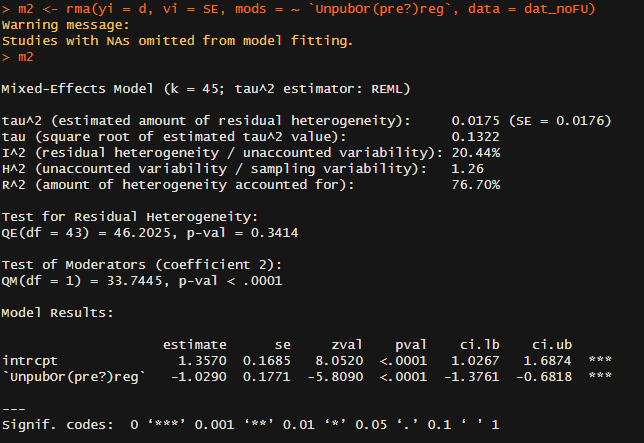
To orientate: in 'Model results' the intercept value gives the estimated effect size when the 'unpub' variable is zero (as I understand it, ~unregistered studies), so d ~ 1.4 (!) for this set of studies. The row below gives the change in effect if you move from 'unpub = 0' to 'unpub = 1' (i.e. ~ registered vs. unregistered studies): this drops effect size by 1, so registered studies give effects of ~0.3. In other words, unregistered and registered studies give dramatically different effects: study registration reduces expected effect size by a factor of 3. [!!!]
The other statistics provided deepen the concern. The included studies have a very high level of heterogeneity (~their effect sizes vary much more than they should by chance). Although HLI attempted to explain this variation with various meta-regressions using features of the intervention, follow-up time, etc., these models left the great bulk of the variation unexplained. Although not like-for-like, here a single indicator of study quality provides compelling explanation for why effect sizes differ so much: it explains three-quarters of the initial variation.[3]
This is easily seen in a grouped forest plot - the top group is the non registered studies, the second group the registered ones:
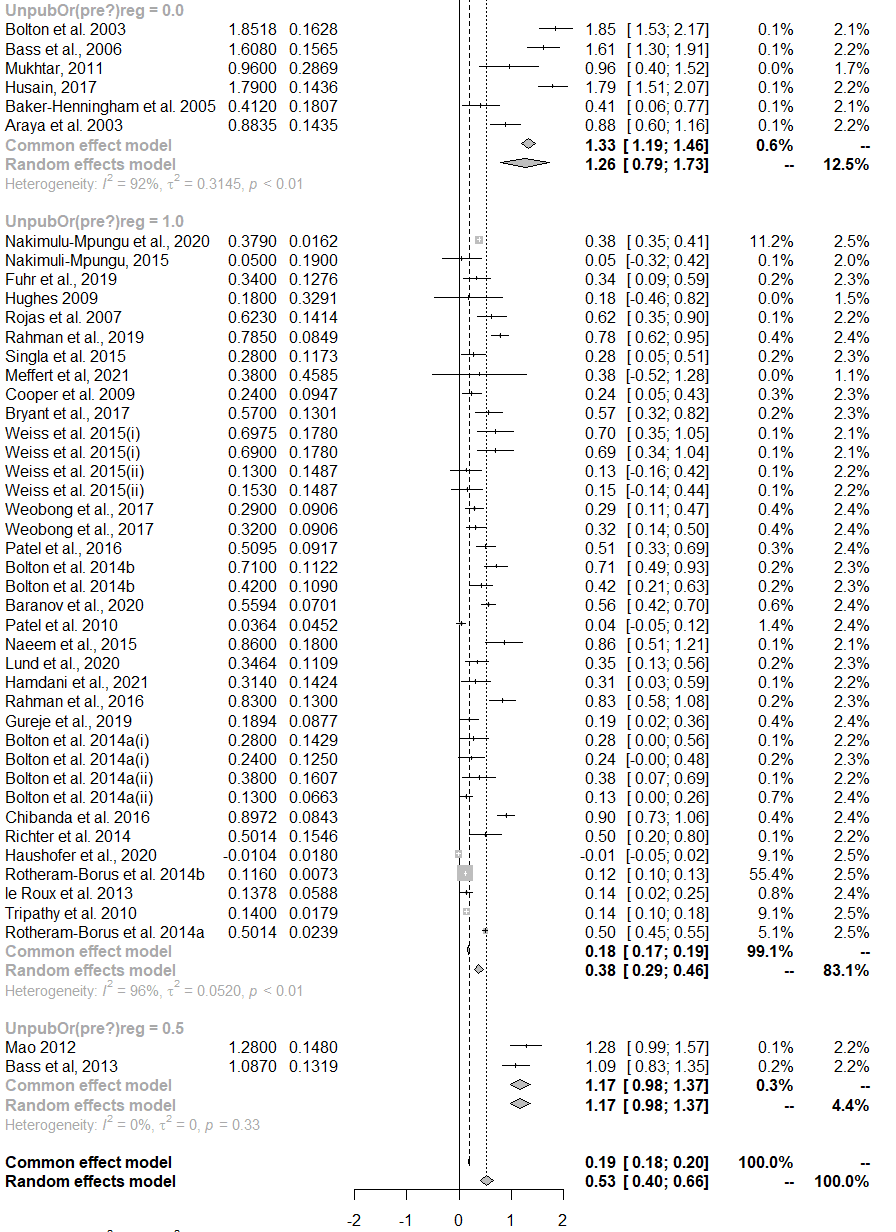
This pattern also perfectly fits the 5 pieces of direct evidence: Bolton 2003 (ES = 1.13), Strongminds RCT (1.72), and Strongminds P2 (1.09) are, as far as I can tell, unregistered. Thurman 2017 (0.09) was registered. Bolton 2007 is also registered, and in fact has an effect size of ~0.5, not 1.79 as HLI reports.[4]
To be clear, I do not think HLI knew of this before I found it out just now. But results like this indicate i) the appraisal of the literature in this analysis gravely off-the-mark - study quality provides the best available explanation for why some trials report dramatically higher effects than others; ii) the result of this oversight is a dramatic over-estimation of likely efficacy of Strongminds (as a ready explanation for the large effects reported in the most 'relevant to strongminds' studies is that these studies were not registered and thus prone to ~200%+ inflation of effect size); iii) this is a very surprising mistake for a diligent and impartial evaluator to make: one would expect careful assessment of study quality - and very sceptical evaluation where this appears to be lacking - to be foremost, especially given the subfield and prior reporting from Strongminds both heavily underline it. This pattern, alas, will prove repetitive.
I also think a finding like this should prompt an urgent withdrawal of both the analysis and recommendation pending further assessment. In honesty, if this doesn't, I'm not sure what ever could.
2:
Indeed excellent researchers overlook things, and although I think both the frequency and severity of things HLI mistakes or overlooks is less-than-excellent, one could easily attribute this to things like 'inexperience', 'trying to do a lot in a hurry', 'limited staff capacity', and so on.
Yet this cannot account for how starkly asymmetric the impact of these mistakes and oversights are. HLI's mistakes are consistently to Strongmind's benefit rather than its detriment, and HLI rarely misses a consideration which could enhance the 'multiple', it frequently misses causes of concern which both undermine both strength and reliability of this recommendation. HLI's award from Givewell deepens my concerns here, as it is consistent with a very selective scepticism: HLI can carefully scruitinize charity evaluations by others it wants to beat, but fails to mete out remotely comparable measure to its own which it intends for triumph.
I think this can also explain how HLI responds to criticism, which I have found by turns concerning and frustrating. HLI makes some splashy claim (cf. 'mission accomplished', 'confident recommendation', etc.). Someone else (eventually) takes a closer look, and finds the surprising splashy claim, rather than basically checking out 'most reasonable ways you slice it', it is highly non-robust, and only follows given HLI slicing it heavily in favour of their bottom line in terms of judgement or analysis - the latter of which often has errors which further favour said bottom line. HLI reliably responds, but the tenor of this response is less 'scientific discourse' and more 'lawyer for defence': where it can, HLI will too often further double down on calls it makes where I aver the typical reasonable spectator would deem at best dubious, and at worst tendentious; where it can't, HLI acknowledges the shortcoming but asserts (again, usually very dubiously) that it isn't that a big deal, so it will deprioritise addressing it versus producing yet more work with the shortcomings familiar to those which came before.
3:
HLI's meta-analysis in no way allays or rebuts the concerns SimonM raised re. Strongminds - indeed, appropriate analysis would enhance many of them. Nor is it the case that the meta-analytic work makes HLI's recommendation robust to shortcomings in the Strongminds-specific evidence - indeed, the cost effectiveness calculator will robustly recommend Strongminds as superior (commonly, several times superior) to GiveDirectly almost no matter what efficacy results (meta-analytic or otherwise) are fed into it. On each.
a) Meta-analysis could help contextualize the problems SimonM identifies in the Strongminds specific data. For example, a funnel plot which is less of a 'funnel' but more of a ski-slope (i.e. massive small study effects/risk of publication bias), and a contour/p-curve suggestive of p-hacking would suggest the field's literature needs to be handled with great care. Finding 'strongminds relevant' studies and direct evidence are marked outliers even relative to this pathological literature should raise alarm given this complements the object-level concerns SimonM presented.
This is indeed true, and these features were present in the studies HLI collected, but HLI failed to recognise it. It may never have if I hadn't gotten curious and did these analyses myself. Said analysis is (relative to the much more elaborate techniques used in HLI's meta-analysis) simple to conduct - my initial 'work' was taking the spreadsheet and plugging it into a webtool out of idle curiosity.[5] Again, this is a significant mistake, adds a directional bias in favour of Strongminds, and is surprising for a diligent and impartial evaluator to make.
b) In general, incorporating meta-analytic results into what is essentially a weighted average alongside direct evidence does not clean either it or the direct evidence of object level shortcomings. If (as here) both are severely compromised, the result remains unreliable.
The particular approach HLI took also doesn't make the finding more robust, as the qualitative bottom line of the cost-effectiveness calculation is insensitive to the meta-analytic result. As-is, the calculator gives strongminds as roughly 12x better than GiveDirectly.[6] If you set both meta-analytic effect sizes to zero, the calculator gives Strongminds as ~7x better than GiveDirectly. So the five pieces of direct evidence are (apparently) sufficient to conclude SM is an extremely effective charity. Obviously this is - and HLI has previously accepted - facially invalid output.
It is not the only example. It is extremely hard for any reduction of efficacy inputs to the model to give a result that Strongminds is worse than Givedirectly. If we instead leave the meta-analytic results as they were but set all the effect sizes of the direct evidence to zero (in essence discounting them entirely - which I think is approximately what should have been done from the start), we get ~5x better than GiveDirectly. If we set all the effect sizes of both meta-analysis and direct evidence to 0.4 (i.e. the expected effects of registered studies noted before), we get ~6x better than Givedirectly. If we set the meta-analytic results to 0.4 and set all the direct evidence to zero we get ~3x GiveDirectly. Only when one sets all the effect sizes to 0.1 - lower than all but ~three of the studies in the meta-analysis - does one approach equipoise.
This result should not surprise on reflection: the CEA's result is roughly proportional to the ~weighted average of input effect sizes, so an initial finding of '10x' Givedirectly or similar would require ~a factor of 10 cut to this average to drag it down to equipoise. Yet this 'feature' should be seen as a bug: in the same way there should be some non-zero value of the meta-analytic results which should reverse a 'many times better than Givedirectly' finding, there should be some non-tiny value of effect sizes for a psychotherapy intervention (or psychotherapy interventions in general) which results in it not being better than GiveDirectly at all.
This does help explain the somewhat surprising coincidence the first charity HLI fully assessed would be one it subsequently announces as the most promising interventions in global health and wellbeing so-far found: rather than a discovery from the data, this finding is largely preordained by how the CEA stacks the deck. To be redundant (and repetitive): i) the cost-effectiveness model HLI is making is unfit-for-purpose, given can produce these absurd results; ii) this introduces a large bias in favour of Strongminds; iii) it is a very surprising mistake for a diligent and impartial evaluator to make - these problems are not hard to find.
They're even easier for HLI to find once they've been alerted to them. I did, months ago, alongside other problems, and suggested the cost-effectiveness analysis and Strongminds recommendation be withdrawn. Although it should have happened then, perhaps if I repeat myself it might happen now.
4:
Accusations of varying types of bad faith/motivated reasoning/intellectual dishonesty should indeed be made with care - besides the difficulty in determination, pragmatic considerations raise the bar still higher. Yet I think the evidence of HLI having less of a finger but more of a fist on the scale throughout its work overwhelms even charitable presumptions made by a saint on its behalf. In footballing terms, I don't think HLI is a player cynically diving to win a penalty, but it is like the manager after the game insisting 'their goal was offside, and my player didn't deserve a red, and.. (etc.)' - highly inaccurate and highly biased. This is a problem when HLI claims itself an impartial referee, especially when it does things akin to awarding fouls every time a particular player gets tackled.
This is even more of a problem precisely because of the complex and interdisciplinary analysis HLI strives to do. No matter the additional analytic arcana, work like this will be largely fermi estimates, with variables being plugged in with little more to inform them than intuitive guesswork. The high degree of complexity provides a vast garden of forking paths available. Although random errors would tend to cancel out, consistent directional bias in model choice, variable selection, and numerical estimates lead to greatly inflated 'bottom lines'.
Although the transparency in (e.g.) data is commendable, the complex analysis also makes scruitiny harder. I expect very few have both the expertise and perseverence to carefully vet HLI analysis themselves; I also expect the vast majority of money HLI has moved has come from those largely taking its results on trust. This trust is ill-placed: HLI's work weathers scruitiny extremely poorly; my experience is very much 'the more you see, the worse it looks'. I doubt many donors following HLI's advice, if they took a peak behind the curtain, would be happy with what they would discover.
If HLI is falling foul of an entrenched status quo, it is not particular presumptions around interventions, nor philosophical abstracta around population ethics, but rather those that work in this community (whether published elsewhere or not) should be even-handed, intellectually honest and trustworthy in all cases; rigorous and reliable commensurate to its expected consequence; and transparently and fairly communicated. I think going against this grain underlies (I suspect) why I am not alone in my concerns, and why HLI has not had the warmest reception. The hope this all changes for the better is not entirely forlorn. But things would have to change a lot, and quickly - and the track record thus far does not spark joy.
- ^
Really surprised I missed this last time, to be honest. Especially because it is the only column title in the spreadsheet highlighted in red.
- ^
Given I will be making complaints about publication bias, file drawer effects, and garden of forking path issues later in the show, one might wonder how much of this applies to my own criticism. How much time did I spend dredging through HLI's work looking for something juicy? Is my file drawer stuffed with analyses I hoped would show HLI in a bad light, actually showed it in a good one, so I don't mention them?
Depressingly, the answer is 'not much' and 'no' respectively. Regressing against publication registration was the second analysis I did on booting up the data again (regressing on active control was the first, mentioned in text). My file drawer subsequent to this is full of checks and double-checks for alternative (and better for HLI) explanations for the startling result. Specifically, and in order:
- I used the no_FU (no follow-ups) data initially for convenience - the full data can include multiple results of the same study at different follow-up points, and these clustered findings are inappropriate to ignore in a simple random effects model. So I checked both by doing this anyway then using a multi-level model to appropriately manage this structure to the data. No change to the key finding.
- Worried that (somehow) I was messing up or misinterpreting the metaregression, I (re)constructed a simple forest plot of all the studies, and confirmed indeed the unregistered ones were visibly off to the right. I then grouped a forest plot by registration variable to ensure it closely agreed with the meta-regression (in main text). It does.
- I then checked the first 10 studies coded by the variable I think is trial registration to check the registration status of those studies matched the codes. Although all fit, I thought the residual risk I was misunderstanding the variable was unacceptably high for a result significant enough to warrant a retraction demand. So I checked and coded all 46 studies by 'registered or not?' to make sure this agreed with my presumptive interpretation of the variable (in text). It does.
- Adding multiple variables to explain an effect geometrically expands researcher degrees of freedom, thus any unprincipled ad hoc investigation by adding or removing them has very high false discovery rates (I suspect this is a major problem with HLI's own meta-regression work, but compared to everything else it merits only a passing mention here). But I wanted to check if I could find ways (even if unprincipled and ad hoc) to attenuate a result as stark as 'unregistered studies have 3x the registered ones'.
- I first tried to replicate HLI's meta-regression work (exponential transformations and all) to see if the registration effect would be attenuated by intervention variables. Unfortunately, I was unable to replicate HLI's regression results from the information provided (perhaps my fault). In any case, simpler versions I constructed did not give evidence for this.
- I also tried throwing in permutations of IPT-or-not (these studies tend to be unregistered, maybe this is the real cause of the effect?), active control-or-not (given it had a positive effect size, maybe it cancels out registration?) and study Standard Error (a proxy - albeit a controversial one - for study size/precision/quality, so if registration was confounded by it, this slightly challenges interpretation). The worst result across all the variations I tried was to drop the effect size of registration by 20% (~ -1 to -0.8), typically via substitution with SE. Omitted variable bias and multiple comparisons mean any further interpretation would be treacherous, but insofar as it provides further support: adding in more proxies for study quality increases explanatory power, and tends to even greater absolute and relative drops in effect size comparing 'highest' versus 'lowest' quality studies.
That said, the effect size is so dramatic to be essentially immune to file-drawer worries. Even if I had a hundred null results I forgot to mention, this finding would survive a Bonferroni correction.
- ^
Obviously 'is the study registered or not'? is a crude indicator of overal quality. Typically, one would expect better measurement (perhaps by including further proxies for underlying study quality) would further increase the explanatory power of this factor. In other words, although these results look really bad, in reality it is likely to be even worse.
- ^
HLI's write up on Bolton 2007 links to this paper (I did double check to make sure there wasn't another Bolton et al. 2007 which could have been confused with this - no other match I could find). It has a sample size of 314, not 31 as HLI reports - I presume a data entry error, although it less than reassuring that this erroneous figure is repeated and subsequently discussed in the text as part of the appraisal of the study: one reason given for weighing it so lightly is its 'very small' sample size.
Speaking of erroneous figures, here's the table of results from this study:
I see no way to arrive at an effect size of d = 1.79 from these numbers. The right comparison should surely be the pre-post difference of GIP versus control in the intention to treat analysis. These numbers give a cohen's d ~ 0.5.
I don't think any other reasonable comparison gets much higher numbers, and definitely not > 3x higher numbers - the differences between any of the groups are lower than the standard deviations, so should bound estimates like Cohen's d to < 1.
[Re. file drawer, I guess this counts as a spot check (this is the only study I carefully checked data extraction), but not a random one: I did indeed look at this study in particular because it didn't match the 'only unregistered studies report crazy-high effects' - an ES of 1.79 is ~2x any other registered study.]
- ^
Re. my worries of selective scepticism, HLI did apply these methods in their meta-analysis of cash transfers, where no statistical suggestion of publication bias or p-hacking was evident.
- ^
This does depend a bit on whether spillover effects are being accounted for. This seems to cut the multiple by ~20%, but doesn't change the qualitative problems with the CEA. Happy to calculate precisely if someone insists.
HLI - but if for whatever reason they're unable or unwilling to receive the donation at resolution, Strongminds.
The 'resolution criteria' are also potentially ambiguous (my bad). I intend to resolve any ambiguity stringently against me, but you are welcome to be my adjudicator.
[To add: I'd guess ~30-something% chance I end up paying out: d = 0.4 is at or below pooled effect estimates for psychotherapy generally. I am banking on significant discounts with increasing study size and quality (as well as other things I mention above I take as adverse indicators), but even if I price these right, I expect high variance.
I set the bar this low (versus, say, d = 0.6 - at the ~ 5th percentile of HLI's estimate) primarily to make a strong rod for my own back. Mordantly criticising an org whilst they are making a funding request in a financially precarious position should not be done lightly. Although I'd stand by my criticism of HLI even if the trial found Strongminds was even better than HLI predicted, I would regret being quite as strident if the results were any less than dramatically discordant.
If so, me retreating to something like "Meh, they got lucky"/"Sure I was (/kinda) wrong, but you didn't deserve to be right" seems craven after over-cooking remarks potentially highly adverse to HLI's fundraising efforts. Fairer would be that I suffer some financial embarrassment, which helps compensate HLI for their injury from my excess.
Perhaps I could have (or should have) done something better. But in fairness to me, I think this is all supererogatory on my part: I do not think my comment is the only example of stark criticism on this forum, but it might be unique in its author levying an expected cost of over $1000 on themselves for making it.]
[Own views]
- I think we can be pretty sure (cf.) the forthcoming strongminds RCT (the one not conducted by Strongminds themselves, which allegedly found an effect size of d = 1.72 [!?]) will give dramatically worse results than HLI's evaluation would predict - i.e. somewhere between 'null' and '2x cash transfers' rather than 'several times better than cash transfers, and credibly better than GW top charities.' [I'll donate 5k USD if the Ozler RCT reports an effect size greater than d = 0.4 - 2x smaller than HLI's estimate of ~ 0.8, and below the bottom 0.1% of their monte carlo runs.]
- This will not, however, surprise those who have criticised the many grave shortcomings in HLI's evaluation - mistakes HLI should not have made in the first place, and definitely should not have maintained once they were made aware of them. See e.g. Snowden on spillovers, me on statistics (1, 2, 3, etc.), and Givewell generally.
- Among other things, this would confirm a) SimonM produced a more accurate and trustworthy assessment of Strongminds in their spare time as a non-subject matter expert than HLI managed as the centrepiece of their activity; b) the ~$250 000 HLI has moved to SM should be counted on the 'negative' rather than 'positive' side of the ledger, as I expect this will be seen as a significant and preventable misallocation of charitable donations.
- Regrettably, it is hard to square this with an unfortunate series of honest mistakes. A better explanation is HLI's institutional agenda corrupts its ability to conduct fair-minded and even-handed assessment for an intervention where some results were much better for their agenda than others (cf.). I am sceptical this only applies to the SM evaluation, and I am pessimistic this will improve with further financial support.
I suspect the 'edge cases' illustrate a large part of the general problem: there are a lot of grey areas here, where finding the right course requires a context-specific application of good judgement. E.g. what 'counts' as being (too?) high status, or seeking to start a 'not serious' (enough?) relationship etc. etc. is often unclear in non-extreme cases - even to the individuals directly involved themselves. I think I agree with most of the factors noted by the OP as being pro tanto cautions, but aliasing them into a bright line classifier for what is or isn't contraindicated looks generally unsatisfactory.
This residual ambiguity makes life harder, as if you can't provide a substitute for good judgement, guidance and recommendations (rather than rulings) may not give great prospects for those with poorer or compromised judgement to bootstrap their way to better decisions. The various fudge factors give ample opportunity for motivated reasoning ("I know generally this would be inappropriate, but I license myself to do it in this particular circumstance"), and sexual attraction is not an archetypal precipitant for wisdom and restraint. Third parties weighing in on perceived impropriety may be less self-serving, but potentially more error-prone, and definitely a lot more acrimonious - I doubt many welcome public or public-ish inquiries or criticism upon the intimate details of their personal lives ("Oh yeah? Maybe before you have a go at me you should explain {what you did/what one of your close friends did/rumours about what someone at your org did/etc.}, which was far worse and your silence then makes you a hypocrite for calling me out now."/ "I don't recall us signing up to 'the EA community', but we definitely didn't sign up for collective running commentary and ceaseless gossip about our sex lives. Kindly consider us 'EA-adjacant' or whatever, and mind your own business"/etc.)
FWIW I have - for quite a while, and in a few different respects - noted that intermingling personal and professional lives is often fraught, and encouraged caution and circumspection for things which narrow the distance between them still further. EA-land can be a chimera of a journal club, a salutatorian model UN, a church youth group, and a swingers party - these aspects are not the most harmonious in concert. There is ample evidence - even more ample recently - that 'encouraging caution' or similar doesn't cut it. I don't think the OP has the right answer, but I do not have great ideas myself: it is much easier to criticise than do better.
The issue re comparators is less how good dropping outliers or fixed effects are as remedies to publication bias (or how appropriate either would be as an analytic choice here all things considered), but the similarity of these models to the original analysis.
We are not, after all, adjusting or correcting the original metaregression analysis directly, but rather indirectly inferring the likely impact of small study effects on the original analysis by reference to the impact it has in simpler models.
The original analysis, of course, did not exclude outliers, nor follow-ups, and used random effects, not fixed effects. So of Models 1-6, model 1 bears the closest similarity to the analysis being indirectly assessed, so seems the most appropriate baseline.
The point about outlier removal and fixed effects reducing the impact of small study effects is meant to illustrate cycling comparators introduces a bias in assessment instead of just adding noise. Of models 2-6, we would expect 2, 4,5 and 6 to be more resilient to small study effects than model 1, because they either remove outliers, use fixed effects, or both (Model 3 should be ~ a wash). The second figure provides some (further) evidence of this, as (e.g.) the random effects models (thatched) strongly tend to report greater effect sizes than the fixed effect ones, regardless of additional statistical method.
So noting the discount for a statistical small study effect correction is not so large versus comparators which are already less biased (due to analysis choices contrary to those made in the original analysis) misses the mark.
If the original analysis had (somehow) used fixed effects, these worries would (largely) not apply. Of course, if the original analysis had used fixed effects, the effect size would have been a lot smaller in the first place.
--
Perhaps also worth noting is - with a discounted effect size - the overall impact of the intervention now becomes very sensitive to linear versus exponential decay of effect, given the definite integral of the linear method scales with the square of the intercept, whilst for exponential decay the integral is ~linear with the intercept. Although these values line up fairly well with the original intercept value of ~ 0.5, they diverge at lower values. If (e.g.) the intercept is 0.3, over a 5 year period the exponential method (with correction) returns ~1 SD years (vs.1.56 originally), whilst the linear method gives ~0.4 SD years (vs. 1.59 originally).
(And, for what it is worth, if you plug in corrected SE or squared values in to the original multilevel meta-regressions, PET/PEESE style, you do drop the intercept by around these amounts either vs. follow-up alone or the later models which add other covariates.)
I have now had a look at the analysis code. Once again, I find significant errors and - once again - correcting these errors is adverse to HLI's bottom line.
I noted before the results originally reported do not make much sense (e.g. they generally report increases in effect size when 'controlling' for small study effects, despite it being visually obvious small studies tend to report larger effects on the funnel plot). When you use appropriate comparators (i.e. comparing everything to the original model as the baseline case), the cloud of statistics looks more reasonable: in general, they point towards discounts, not enhancements, to effect size: in general, the red lines are less than 1, whilst the blue ones are all over the place.

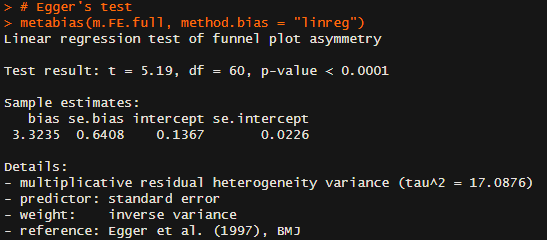
However, some findings still look bizarre even after doing this. E.g. Model 13 (PET) and model 19 (PEESE) not doing anything re. outliers, fixed effects, follow-ups etc, still report higher effects than the original analysis. These are both closely related to the eggers test noted before: why would it give a substantial discount, yet these a mild enhancement?
Happily, the code availability means I can have a look directly. All the basic data seems fine, as the various 'basic' plots and meta-analyses give the right results. Of interest, the Egger test is still pointing the right way - and even suggests a lower intercept effect size than last time (0.13 versus 0.26):
PET gives highly discordant findings:
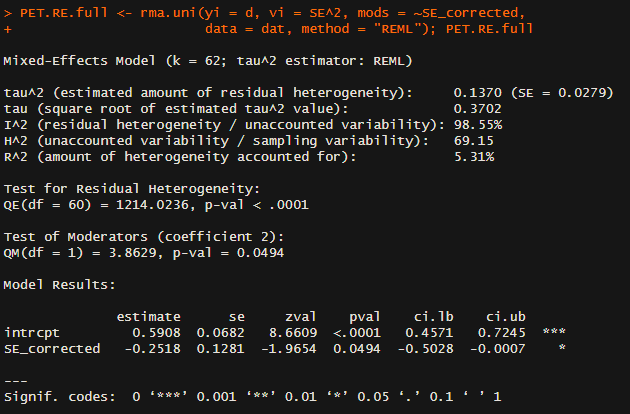
You not only get a higher intercept (0.59 versus 0.5 in the basic random effects model), but the coefficient for standard error is negative: i.e. the regression line it draws slopes the opposite way to Eggers, so it predicts smaller studies give smaller, not greater, effects than larger ones. What's going on?
The moderator (i.e. ~independent variable) is 'corrected' SE. Unfortunately, this correction is incorrect (line 17 divides (n/2)^2 by itself, where the first bracket should be +, not *), so it 'corrects' a lot of studies to SE = 1 exactly:
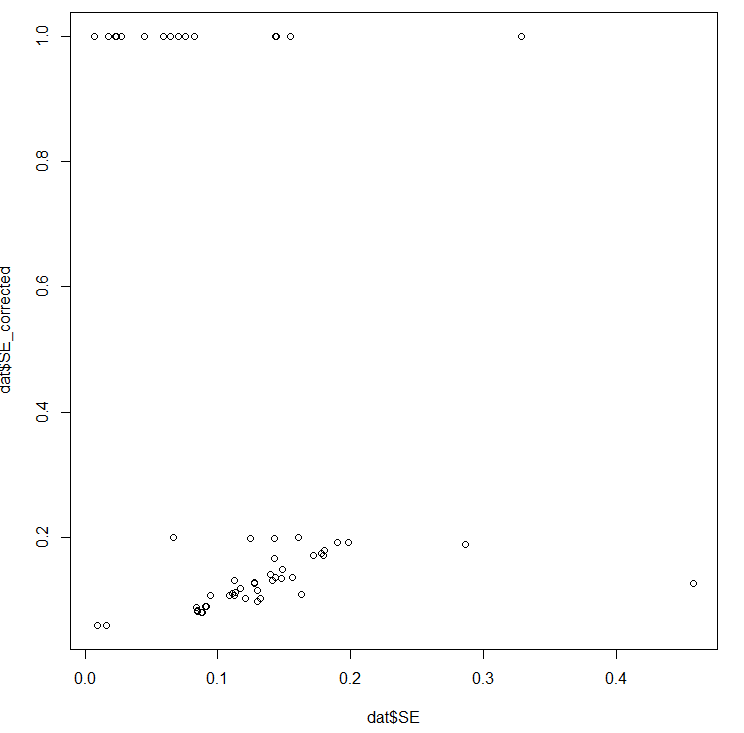
When you use this in a funnel plot, you get this:

Thus these aberrant results (which happened be below the mean effect size) explain why the best fit line now points in the opposite direction. All the PET analyses are contaminated by this error, and (given PEESE squares these values) so are all the PEESE analyses. When debugged, PET shows an intercept lower than 0.5, and the coefficient for SE pointing in the right direction:

Here's the table of corrected estimates applied to models 13 - 24: as you can see, correction reduces the intercept in all models, often to substantial degrees (I only reported to 2 dp, but model 23 was marginally lower). Unlike the original analysis, here the regression slopes generally point in the right direction.

The same error appears to be in the CT analyses. I haven't done the same correction, but I would guess the bizarre readings (e.g. the outliers of 70x or 200x etc. when comparing PT to CT when using these models) would vanish once it is corrected.
So, when correcting the PET and PEESE results, and use the appropriate comparator (Model 1, I forgot to do this for models 2-6 last time), we now get this:
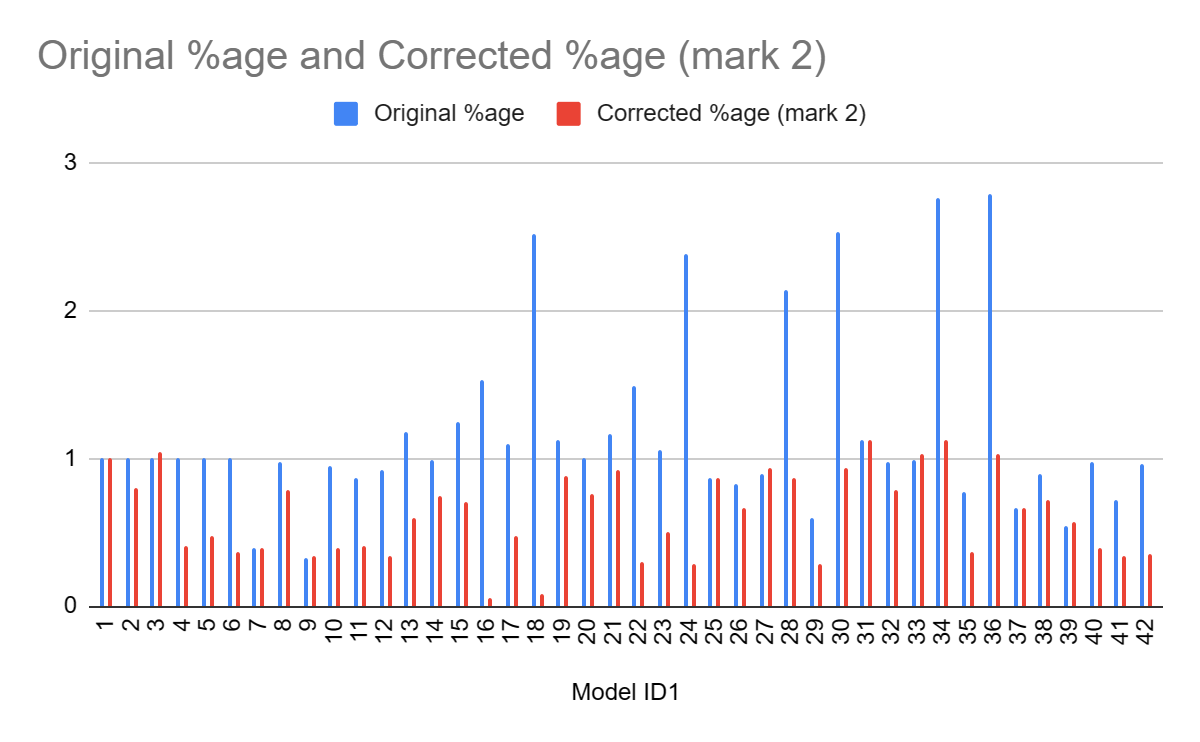
Now interpretation is much clearer. Rather than 'all over the place, but most of the models basically keep the estimate the same', it is instead 'across most reasonable ways to correct or reduce the impact of small study effects, you see substantial reductions in effect (the avg across the models is ~60% of the original - not a million miles away from my '50%?' eyeball guess.) Moreover, the results permit better qualitative explanation.
- On the first level, we can make our model fixed or random effects, fixed effects are more resilient to publication bias (more later), and we indeed find changing from random effects to fixed effect (i.e. model 1 to model 4) reduces effect size by a bit more than 2.
- On the second level, we can elect for different inclusion criteria: we could remove outliers, or exclude follow-ups. The former would be expected to partially reduce small study effects (as outliers will tend to be smaller studies reporting surprisingly high effects), whilst the later does not have an obvious directional effect - although one should account for nested outcomes, this would be expected to distort the weights rather than introduce a bias in effect size. Neatly enough, we see outlier exclusion does reduce effect size (Model 2 versus Model 1) but not followups or not (model 3 versus model 1). Another neat example of things lining up is you would expect FE to give a greater correction than outlier removal (as FE is strongly discounting smaller studies across the board, rather than removing a few of the most remarkable ones), and this is what we see (Model 2 vs. Model 4)
- Finally, one can deploy a statistical technique to adjust for publication bias. There are a bunch of methods to do this: PET, PEESE, Rucker's limit, P curve, and selection models. All of these besides the P curve give a discount to the original effect size (model 7, 13,19,25,37 versus model 31).
- We can also apply these choices in combination, but essentially all combinations point to a significant downgrade in effect size. Furthermore, the combinations allow us to better explain discrepant findings. Only models 3, 31, 33, 35, 36 give numerically higher effect sizes. As mentioned before, model 3 only excludes follow-ups, so would not be expected to be less vulnerable to small study effects. The others are all P curve analyses, and P curves are especially sensitive to heterogeneity: the two P curves which report discounts are those with outliers removed (Model 32, 35), supporting this interpretation.
With that said, onto Joel's points.
1. Discarding (better - investigating) bizarre results
I think if we discussed this beforehand and I said "Okay, you've made some good points, I'm going to run all the typical tests and publish their results." would you have said have advised me to not even try, and instead, make ad hoc adjustments. If so, I'd be surprised given that's the direction I've taken you to be arguing I should move away from.
You are correct I would have wholly endorsed permuting all the reasonable adjustments and seeing what picture emerges. Indeed, I would be (and am) happy with 'throwing everything in' even if some combinations can't really work, or doesn't really make much sense (e.g. outlier rejection + trim and fill).
But I would have also have urged you to actually understand the results you are getting, and querying results which plainly do not make sense. That we're still seeing the pattern of "Initial results reported don't make sense, and I have to repeat a lot of the analysis myself to understand why (and, along the way, finding the real story is much more adverse than HLI presents)" is getting depressing.
The error itself for PET and PEESE is no big deal - "I pressed the wrong button once when coding and it messed up a lot of my downstream analysis" can happen to anyone. But these results plainly contradicted both the naked eye (they not only give weird PT findings but weird CT findings: by inspection the CT is basically a negative control for pub bias, yet PET-PEESE typically finds statistically significant discounts), the closely-related Egger's test (disagreeing with respect to sign), and the negative coefficients for the models (meaning they are sloping in the opposite direction) are printed in the analysis code.
I also find myself inclined to less sympathy here because I didn't meticulously inspect every line of analysis code looking for trouble (my file drawer is empty). I knew the results being reported for these analysis could not be right, so I zeroed in on it expecting there was an error. I was right.
2. Comparators
When I do this, and again remove anything that doesn't produce a discount for psychotherapy, the average correction leads to a 6x cost-effectiveness ratio of PT to CT. This is a smaller shift than you seem to imply.
9.4x -> ~6x is a drop of about one third, I guess we could argue about what increment is large or small. But more concerning is the direction of travel: taking the 'CT (all)' comparator.
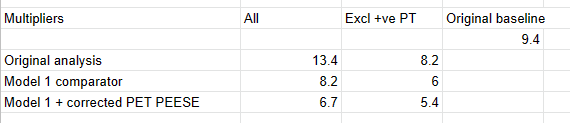
If we do not do my initial reflex and discard the PT favouring results, then we see adding the appropriate comparator and fixing the statistical error ~ halves the original multiple. If we continue excluding the "surely not" +ve adjustments, we're still seeing a 20% drop with the comparator, and a further 10% increment with the right results for PT PET/PEESE.
How many more increments are there? There's at least one more - the CT PET/PEESE results are wrong, and they're giving bizarre results in the spreadsheet. Although I would expect diminishing returns to further checking (i.e. if I did scour the other bits of the analysis, I expect the cumulative error is smaller or neutral), but the 'limit value' of what this analysis would show if there were no errors doesn't look great so far.
Maybe it would roughly settle towards the average of ~ 60%, so 9.4*0.6 = 5.6. Of course, this would still be fine by the lights of HLI's assessment.
3. Cost effectiveness analysis
My complete guess is that if StrongMinds went below 7x GiveDirectly we'd qualitatively soften our recommendation of StrongMinds and maybe recommend bednets to more donors. If it was below 4x we'd probably also recommend GiveDirectly. If it was below 1x we'd drop StrongMinds. This would change if / when we find something much more (idk: 1.5-2x?) cost-effective and better evidenced than StrongMinds.
However, I suspect this is beating around the bush -- as I think the point Gregory is alluding to is "look at how much their effects appear to wilt with the slightest scrutiny. Imagine what I'd find with just a few more hours."
If that's the case, I understand why -- but that's not enough for me to reshuffle our research agenda. I need to think there's a big, clear issue now to ask the team to change our plans for the year. Again, I'll be doing a full re-analysis in a few months.
Thank you for the benchmarks. However, I mean to beat both the bush and the area behind it.
The first things first, I have harped on about the CEA because it is is bizarre to be sanguine about significant corrections because 'the CEA still gives a good multiple' when the CEA itself gives bizarre outputs (as noted before). With these benchmarks, it seems this analysis, on its own terms, is already approaching action relevance: unless you want to stand behind cycling comparators (which the spreadsheet only does for PT and not CT, as I noted last time), then this + the correction gets you below 7x. Further, if you want to take SM effects as relative to the meta-analytic results (rather take their massively outlying values), you get towards 4x (e.g. drop the effect size of both meta-analyses by 40%, then put the SM effect sizes at the upper 95% CI). So there's already a clear motive to investigate urgently in terms of what you already trying to do.
The other reason is the general point of "Well, this important input wilts when you look at it closely - maybe this behaviour generalises". Sadly, we don't really need to 'imagine' what I would find with a few more hours: I just did (and on work presumably prepared expecting I would scrutinise it), and I think the results speak for themselves.
The other parts of the CEA are non-linear in numerous ways, so it is plausible that drops of 50% in intercept value lead to greater than 50% drops in the MRA integrated effect sizes if correctly ramified across the analysis. More importantly, the thicket of the guestimate gives a lot of forking paths available - given it seems HLI clearly has had a finger on the scale, you may not need many more relatively gentle (i.e. 10%-50%) pushes upwards to get very inflated 'bottom line multipliers'.
4. Use a fixed effects model instead?
As Ryan notes, fixed effects are unconventional in general, but reasonable in particular when confronted with considerable small study effects. I think - even if one had seen publication bias prior to embarking on the analysis - sticking with random effects would have been reasonable.
Thanks for this, Joel. I look forward to reviewing the analysis more fully over the weekend, but I have three major concerns with what you have presented here.
1. A lot of these publication bias results look like nonsense to the naked eye.
Recall the two funnel plots for PT and CT (respectively):
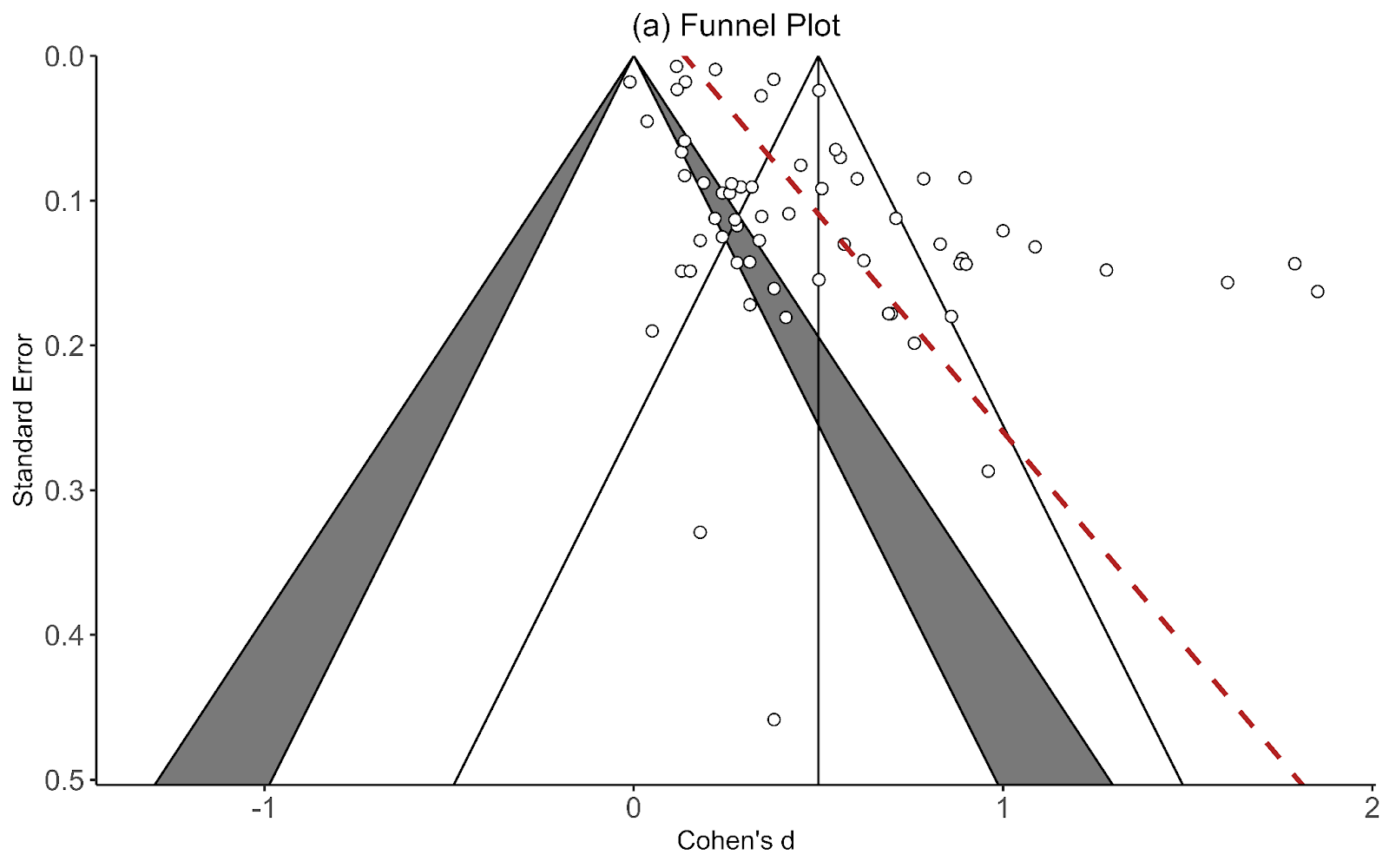
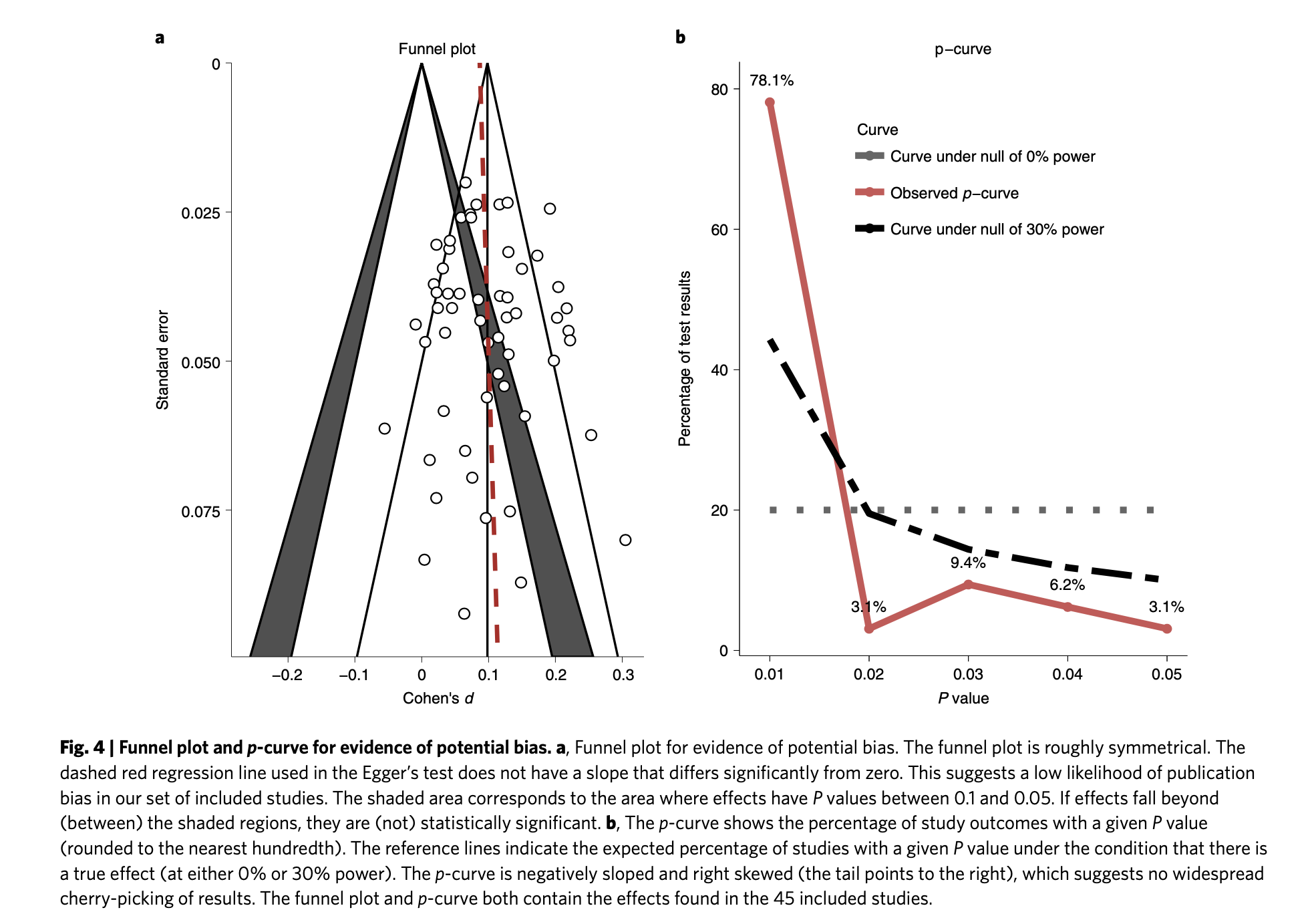
I think we're all seeing the same important differences: the PT plot has markers of publication bias (asymmetry) and P hacking (clustering at the P<0.05 contour, also the p curve) visible to the naked eye; the CT studies do not really show this at all. So heuristically, we should expect statistical correction for small study effects to result in:
- In absolute terms, the effect size for PT should be adjusted downwards
- In comparative terms, the effect size for PT should be adjusted downwards more than the CT effect size.
If a statistical correction does the opposite of these things, I think we should say its results are not just 'surprising' but 'unbelievable': it just cannot be true that, given the data we see being fed into the method it should lead us to conclude this CT literature is more prone to small-study effects than this PT one; nor (contra the regression slope in the first plot), the effect size for PT should be corrected upwards.
Yet many of the statistical corrections you have done tend to fail one or both of these basically-diagnostic tests of face validity. Across all the different corrections for PT, on average the result is a 30% increase in PT effect size (only trim and fill and selection methods give families of results where the PT effect size is reduced). Although (mostly) redundant, these are also the only methods which give a larger drop to PT than CT effect size.
As comments everywhere on this post have indicated, heterogeneity is tricky. If (generally) different methods all gave discounts, but they were relatively small (with the exception of one method like a Trim and Fill which gave a much steeper one), I think the conclusions you drew above would be reasonable. However, for these results, the ones that don't make qualitative sense should be discarded, and the the key upshot should be: "Although a lot of statistical corrections give bizarre results, the ones which do make sense also tend to show significant discounts to the PT effect size".
2. The comparisons made (and the order of operations to get to them) are misleading
What is interesting though, is although in % changes correction methods tend to give an increase to PT effect size, the effect sizes themselves tend to be lower: the average effect size across analyses is 0.36, ~30% lower than the pooled estimate of 0.5 in the funnel plot (in contrast, this is 0.09 - versus 0.1, for CT effect size).
This is the case because the % changes are being measured, not against the single reference value of 0.5 in the original model, but the equivalent model in terms of random/fixed, outliers/not, etc. but without any statistical correction technique. For example: row 13 (Model 10) is Trim-and-Fill correction for a fixed effect model using the full data. For PT, this effect size is 0.19. The % difference is calculated versus row 7 (Model 4), a fixed effect model without Trim-and-Fill (effect = 0.2) not the original random effects analysis (effect = 0.5). Thus the % of reference effect is 95% not 40%. In general, comparing effect sizes to row 4 (Model ID 1) generally gets more sensible findings, and also generally more adverse ones. re. PT pub bias correction:

In terms of (e.g.) assessing the impact of Trim and Fill in particular, it makes sense to compare like with like. Yet presumably what we care about to ballparking the estimate of publication bias in general - and for the comparisons made in the spreadsheet mislead. Fixed effect models (ditto outlier exclusion, but maybe not follow-ups) are already an (~improvised) means of correcting for small study effects, as they weigh them in the pooled estimate much less than random effects models. So noting Trim-and-Fill only gives a 5% additional correction in this case buries the lede: you already halved the effect by moving to a fixed effect model from a random effect model, and the most plausible explanation why fixed effect modelling limits distortion by small study effects.
This goes some way to explaining the odd findings for statistical correction above: similar to collider/collinearity issues in regression, you might get weird answers of the impact of statistical techniques when you are already partly 'controlling for' small study effects. The easiest example of this is combining outlier removal with trim and fill - the outlier removal is basically doing the 'trim' part already.
It also indicates an important point your summary misses. One of the key stories in this data is: "Generally speaking, when you start using techniques - alone or in combination - which reduce the impact of publication bias, you cut around 30% of the effect size on average for PT (versus 10%-ish for CT)".
3. Cost effectiveness calculation, again
'Cost effectiveness versus CT' is a unhelpful measure to use when presenting these results: we would first like to get a handle on the size of the small study effect in the overall literature, and then see what ramifications it has for the assessment and recommendations of strongminds in particular. Another issue is these results doesn't really join up with the earlier cost effectiveness assessment in ways which complicate interpretation. Two examples:
- On the guestimate, setting the meta-regressions to zero effect still results in ~7x multiples for Strongminds versus cash transfers. This spreadsheet does a flat percentage of the original 9.4x bottom line (so a '0% of previous effect' correction does get the multiple down to zero). Being able to get results which give <7x CT overall is much more sensible than what the HLI CEA does, but such results could not be produced if we corrected the effect sizes and plugged them back into the original CEA.
- Besides results being incongruous, the methods look incongruous too. The outliers being excluded in some analyses include strong-minds related papers later used in the overall CE calculation to get to the 9.4 figure. Ironically, exclusion would have been the right thing to do originally, as including the papers help derive the pooled estimate and then again as independent inputs into the CEA double counts them. Alas two wrongs do not make a right: excluding them in virtue of outlier effects seems to imply either: i) these papers should be discounted generally (so shouldn't be given independent weight in the CEA); ii) they are legit, but are such outliers the meta-analysis is actually uninformative to assess the effect of the particular interventions they investigate.
More important than this, though, is the 'percentage of what?' issue crops up again: the spreadsheet uses relative percentage change to get a relative discount vs. CT, but it uses the wrong comparator to calculate the percentages.
Lets look at row 13 again, where we are conducting a fixed effects analysis with trim-and-fill correction. Now we want to compare PT and CT: does PT get discounted more than CT? As mentioned before, for PT, the original random effects model gives an effect size of 0.5, and with T'n'F+Fixed effects the effect size is 0.19. For CT, the original effect size is 0.1, and with T'n'F +FE, it is still 0.1. In relative terms, as PT only has 40% of the previous effect size (and CT 100% of the effect size), this would amount to 40% of the previous 'multiple' (i.e. 3.6x).
Instead of comparing them to the original estimate (row 4), it calculates the percentages versus a fixed effect but not T'n'F analysis for PT (row 7). Although CT here is also 0.1, PT in this row has an effect size of 0.2, so the PT percentage is (0.19/0.2) 95% versus (0.1/0.1) 100%, and so the calculated multiple of CT is not 3.6 but 9.0.
The spreadsheet is using the wrong comparison, as we care about whether the multiple between PT and CT is sensitive to different analyses, relative sensitivity to one variation (T'n'F) conditioned on another (fixed effect modelling). Especially when we're interested in small study effects and the conditioned on effect likely already reduces those.
If one recalculates the bottom line multiples using the first model as the comparator, the results are a bit less weird, but also more adverse to PT. Note the effect is particularly reliable for T'n'F (ID 7-12) and selection measures (ID 37-42), which as already mentioned are the analysis methods which give qualitatively believable findings.
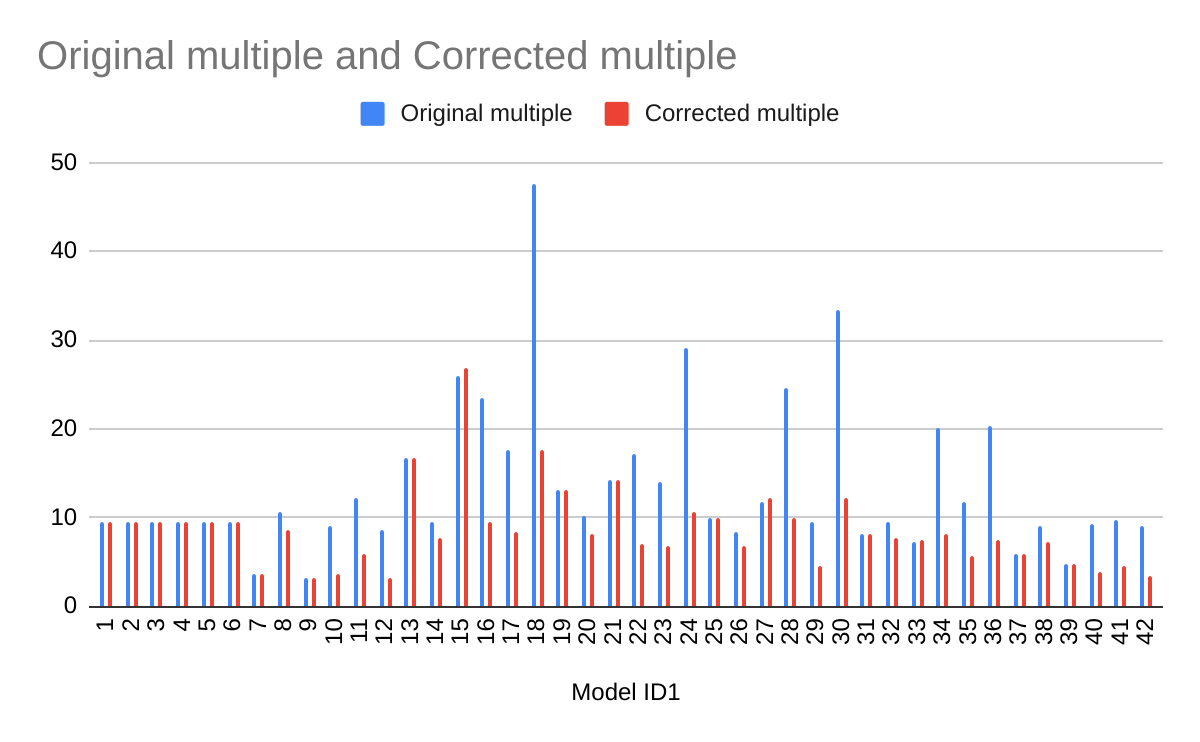
Of interest, the spreadsheet only makes this comparator error for PT: for CT, whether all or lumped (column I and L) makes all of its percentage comparisons versus the original model (ID 1). I hope (and mostly expect) this is a click-and-drag spreadsheet error (or perhaps one of my understanding), rather than my unwittingly recovering an earlier version of this analysis.
Summing up
I may say more next week, but my impressions are
- In answer to the original post title, I think the evidence for Strongminds is generally weak, equivocal, likely compromised, and definitely difficult to interpret.
- Many, perhaps most (maybe all?) of the elements used in HLI's recommendation of strongminds do not weather scrutiny well. E.g.
- Publication bias issues discussed in the comments here.
- The index papers being noted outliers even amongst this facially highly unreliable literature.
- The cost effectiveness guestimate not giving sensible answers when you change its inputs.
- I think HLI should withdraw their recommendation of Strongminds, and mostly go 'back to the drawing board' on their assessments and recommendations. The current recommendation is based on an assessment with serious shortcomings in many of its crucial elements. I regret I suspect if I looked into other things I would see still more causes of concern.
- The shortcomings in multiple elements also make criticism challenging. Although HLI thinks the publication bias is not big enough of an effect to withdraw the recommendation, it what publication bias would be big enough, or indeed in general what evidence would lead them to change their minds. Their own CEA is basically insensitive to the meta-analysis, giving 'SM = 7x GD' even if the effect size was corrected all the way to zero. Above Joel notes even at 'only' SM = 3-4GD it would still generally be their top recommendation. So by this logic, the only decision-relevance this meta-analysis has is confirming the effect isn't massively negative. I doubt this is really true, but HLI should have a transparent understanding (and, ideally, transparent communication) of what their bottom line is actually responsive to.
- One of the commoner criticisms of HLI is it is more a motivated reasoner than an impartial evaluator. Although its transparency in data (and now code) is commendable, overall this episode supports such an assessment: the pattern which emerges is a collection of dubious-to-indefensible choices made in analysis, which all point in the same direction (i.e. favouring the Strongminds recommendation); surprising incuriousity about the ramifications or reasonableness of these analytic choices; and very little of this being apparent from the public materials, emerging instead in response to third party criticism or partial replication.
- Although there are laudable improvements contained in Joel's summary above, unfortunately (per my earlier points) I take it as yet another example of this overall pattern. The reasonable reaction to "Your publication bias corrections are (on average!) correcting the effect size upwards, and the obviously skewed funnel plot less than the not obviously skewed one" is not "Well, isn't that surprising - I guess there's no clear sign of trouble with pub bias in our recommendation after all", but "This doesn't make any sense".
- I recommend readers do not rely upon HLIs recommendations or reasoning without carefully scrutinising the underlying methods and data themselves.
Hello Joel,
0) My bad re rma.rv output, sorry. I've corrected the offending section. (I'll return to some second order matters later).
1) I imagine climbing in Mexico is more pleasant than arguing statistical methods on the internet, so I've attempted to save you at least some time on the latter by attempting to replicate your analysis myself.
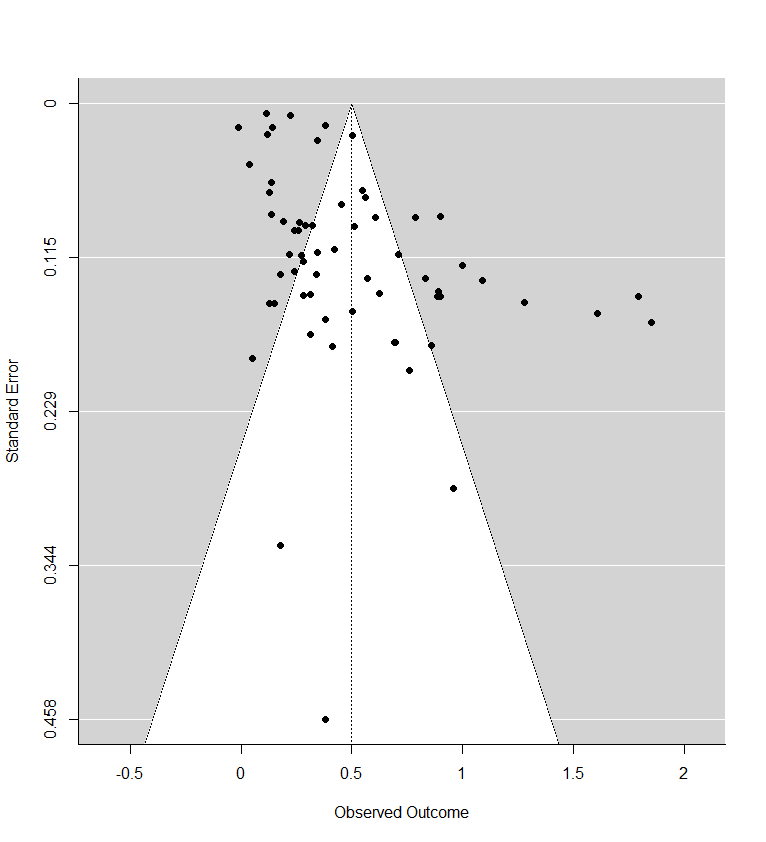
This attempt was only partially successful: I took the 'Lay or Group cleaner' sheet and (per previous comments) flipped the signs where necessary so only Houshofer et al. shows a negative effect. Plugging this into R means I get basically identical results for the forest plot (RE mean 0.50 versus 0.51) and funnel plot (Eggers lim value 0.2671 vs. 0.2670). I get broadly similar but discordant values for the univariate linear and exp decay, as well as model 1 in table 2 [henceforth 'model 3'] (intercepts and coefficients ~ within a standard error of the write-up's figures), and much more discordant values for the others in table 2.
I expect this 'failure to fully replicate' is mostly owed to a mix of i) very small discrepancies between the datasets we are working off are likely to be amplified in more complex analysis than simpler forest plots etc. ii) I'd guess the covariates would be much more discrepant, and there are more degrees of freedom in how they could be incorporated, so it is much more likely we aren't doing exactly the same thing (e.g. 'Layness' in my sheet seems to be ordinal - values of 0-3 depending on how well trained the provider was, whilst the table suggests it was coded as categorical (trained or not)in the original analysis. Hopefully it is 'close enough' for at least some indicative trends not to be operator error. In the spirit of qualified reassurance here's my funnel plot:
2) Per above, one of the things I wanted to check is whether indeed you see large drops in effect size when you control for small studies/publication bias/etc. You can't neatly merge (e.g.) Egger into meta-regression (at least, I can't), but I can add in study standard error as a moderator. Although there would be many misgivings of doing this vs. (e.g.) some transformation (although I expect working harder to linearize etc. would accentuate any effects), there are two benefits: i) extremely simple, ii) it also means the intercept value is where SE = 0, and so gives an estimate of what a hypothetical maximally sized study would suggest.
Adding in SE as a moderator reduces the intercept effect size by roughly half (model 1: 0.51 -> 0.25; model 2: 0.42 -> 0.23; model 3: 0.69 ->0.36). SE inclusion has ~no effect on the exponential model time decay coefficient, but does seem to confound the linear decay coefficient (effect size down by a third, so no longer a significant predictor) and the single group or individual variable I thought I could helpfully look at (down by ~20%). I take this as suggestive there is significant confounding of results by small study effects, and bayesian best guess correction is somewhere around a 50% discount.
3) As previously mentioned, if you plug this into the guestimate you do not materially change the CEA (roughly 12x to 9x if you halve the effect sizes), but this is because this CEA will return strongminds at least seven times better than cash transfers even if the effect size in the MRAs are set to zero. I did wonder how negative the estimate would have to be to change the analysis, but the gears in the guestimate include logs so a lot of it errors if you feed in negative values. I fear though, if it were adapted, it would give absurd results (e.g. still recommending strongminds even if the MRAs found psychotherapy exacerbated depression more than serious adverse life events).
4) To have an empty file-drawer, I also looked at 'source' to see whether cost survey studies gave higher effects due to the selection bias noted above. No: non-significantly numerically lower.
5) So it looks like the publication bias is much higher than estimated in the write-up: more 50% than 15%. I fear part of the reason for this discrepancy is the approach taken in Table A.2 is likely methodologically and conceptually unsound. I'm not aware of a similar method in the literature, but it sounds like what you did is linearly (?meta)regress g on N for the metaPsy dataset (at least, I get similar figures when I do this, although my coefficient is 10x larger). If so, this doesn't make a lot of sense to me - SE is non-linear in N, the coefficient doesn't limit appropriately (e.g. an infinitely large study has +inf or -inf effects depending on which side of zero the coefficient is), and you're also extrapolating greatly out of sample for the correction between average study sizes. The largest study in MetaPsy is ~800 (I see two points on my plot above 650), but you are taking the difference of N values at ~630 and ~2700.
Even more importantly, it is very odd to use a third set of studies to make the estimate versus the two literatures you are evaluating (given an objective is to compare the evidence bases, why not investigate them directly?) Treating them alike also assumes they share the same degree of small study effects - there are just at different points 'along the line' because one tends to have bigger studies than the other. It would seem reasonable to consider that the fields may differ in their susceptibility to publication bias and p-hacking, so - controlling for N - cash transfer studies are less biased than psychotherapy ones. As we see from the respective forest plots, this is clearly the case - the regression slope for psychotherapy is like 10x or something as slope-y as the one for cash transfers.
(As a side note, MetaPsy lets you shove all of their studies into a forest plot, which looks approximately as asymmetric as the one from the present analysis:)
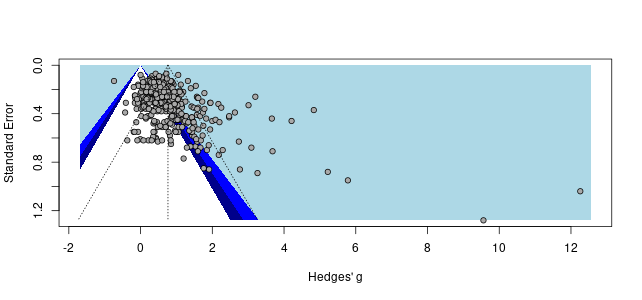
6) Back to the meta stuff.
I don't suspect either you or HLI of nefarious or deceptive behaviour (besides priors, this is strongly ruled against by publishing data that folks could analyse for themselves). But I do suspect partiality and imperfect intellectual honesty. By loose analogy, rather than a football referee who is (hopefully) unbiased but perhaps error prone, this is more like the manager of one of the teams claiming "obviously" their side got the rough end of the refereeing decisions (maybe more error prone in general, definitely more likely to make mistakes favouring one 'side', but plausibly/probably sincere), but not like (e.g.) a player cynically diving to try and win a penalty. In other words, I suspect - if anything - you mostly pulled the wool over your own eyes, without really meaning to.
One reason this arises is, unfortunately, the more I look into things the more cause for concern I find. Moreover, the direction of concern re. these questionable-to-dubious analysis choices strongly tend in the direction of favouring the intervention. Maybe I see what I want to, but can't think of many cases where the analysis was surprisingly incurious about a consideration which would likely result in the effect size being adjusted upwards, nor where a concern about accuracy and generalizability could be further allayed with an alternative statistical technique (one minor example of the latter - it looks like you coded Mid and Low therapy as categoricals when testing sensitivity to therapyness: if you ordered them I expect you'd get a significant test for trend).
I'm sorry again for mistaking the output you were getting, but - respectfully - it still seems a bit sus. It is not like one should have had a low index of suspicion for lots of heterogeneity given how permissively you were including studies; although Q is not an oracular test statistic, P<0.001 should be an prompt to look at this further (especially as you can look at how Q changes when you add in covariates, and lack of great improvement when you do is a further signal); and presumably the very low R2 values mentioned earlier would be another indicator.
Although meta-analysis as a whole is arduous, knocking up a forest and funnel plot to have a look (e.g. whether one should indeed use random vs. fixed effects, given one argument for the latter is they are less sensitive to small study effects) is much easier: I would have no chance of doing any of this statistical assessment without all your work getting the data in the first place; with it, I got the (low-quality, but informative) plots in well under an hour, and do what you've read above took a morning.
I had the luxury of not being on a deadline, but I'm afraid a remark like "I didn't feel like I had time to put everything in both CEAs, explain it, and finish both CEAs before 2021 ended (which we saw as important for continuing to exist)" inspires sympathy but not reassurance on objectivity. I would guess HLI would have seen not only the quality and timeliness of the CEAs as important to its continued existence, but also the substantive conclusions they made: "We find the intervention we've discovered is X times better than cash transfers, and credibly better than Givewell recs" seems much better in that regard than (e.g.) "We find the intervention we previously discovered and recommended, now seems inferior to cash transfers - leave alone Givewell top charities - by the lights of our own further assessment".
Besides being less pleasant, speculating over intentions is much less informative than the actual work itself. I look forward to any further thoughts you have on whether I am on the right track re. correction for small study effects, and I hope future work will indeed show this intervention is indeed as promising as your original analysis suggests.

Hello Jason,
With apologies for delay. I agree with you that I am asserting HLI's mistakes have further 'aggravating factors' which I also assert invites highly adverse inference. I had hoped the links I provided provided clear substantiation, but demonstrably not (my bad). Hopefully my reply to Michael makes them somewhat clearer, but in case not, I give a couple of examples below with as best an explanation I can muster.
I will also be linking and quoting extensively from the Cochrane handbook for systematic reviews - so hopefully even if my attempt to clearly explain the issues fail, a reader can satisfy themselves my view on them agrees with expert consensus. (Rather than, say, "Cantankerous critic with idiosyncratic statistical tastes flexing his expertise to browbeat the laity into aquiescence".)
0) Per your remarks, there's various background issues around reasonableness, materiality, timeliness etc. I think my views basically agree with yours. In essence: I think HLI is significantly 'on the hook' for work (such as the meta-analysis) it relies upon to make recommendations to donors - who will likely be taking HLI's representations on its results and reliability (cf. HLI's remarks about its 'academic research', 'rigour' etc.) on trust. Discoveries which threaten the 'bottom line numbers' or overall reliability of this work should be addressed with urgency and robustness appropriate to their gravity. "We'll put checking this on our to-do list" seems fine for an analytic choice which might be dubious but of unclear direction and small expected magnitude. As you say, a typo which where corrected reduces the bottom line efficacy by ~ 20% should be done promptly.
The two problems I outlined 6 months ago each should have prompted withdrawal/suspension of both the work and the recommendation unless and until they were corrected.[1] Instead, HLI has not made appropriate corrections, and instead persists in misguiding donations and misrepresenting the quality of its research on the basis of work it has partly acknowledged (and which reasonable practicioners would overwhelmingly concur) was gravely compromised.[2]
1.0) Publication bias/Small study effects
It is commonplace in the literature for smaller studies to show different (typically larger) effect sizes than large studies. This is typically attributed to a mix of factors which differentially inflate effect size in smaller studies (see), perhaps the main one being publication bias: although big studies are likely to be published "either way", investigators may not finish (or journals may not publish) smaller studies reporting negative results.
It is extremely well recognised that these effects can threaten the validity of meta-analysis results. If you are producing something (very roughly) like an 'average effect size' from your included studies, the studies being selected for showing a positive effect means the average is inflated upwards. This bias is very difficult to reliably adjust for or 'patch' (more later), but it can easily be large enough to mean "Actually, the treatment has no effect, and your meta-analysis is basically summarizing methodological errors throughout the literature".
Hence why most work on this topic stresses the importance of arduous efforts in prevention (e.g trying really hard to find 'unpublished' studies) and diagnosis (i.e. carefully checking for statistical evidence of this problem) rather than 'cure' (see eg.). If a carefully conducted analysis nonetheless finds stark small study effects, this - rather than the supposed ~'average' effect - would typically be (and should definitely be) the main finding: "The literature is a complete mess - more, and much better, research needed".
As in many statistical matters, a basic look at your data can point you in the right direction. For meta-analysis, this standard is a forest plot:
To orientate: each row is a study (presented in order of increasing effect size), and the horizontal scale is effect size (where to the right = greater effect size favouring the intervention). The horizontal bar for each study is gives the confidence interval for the effect size, with the middle square marking the central estimate (also given in the rightmost column). The diamond right at the bottom is the pooled effect size - the (~~)[3] average effect across studies mentioned earlier.
Here, the studies are all over the map, many of which do not overlap with one another, nor with the pooled effect size estimate. In essence, dramatic heterogeneity: the studies are reporting very different effect sizes from another. Heterogeneity is basically a fact of life in meta-analysis, but a forest plot like this invites curiousity (or concern) about why effects are varying quite this much. [I'm going to be skipping discussion of formal statistical tests/metrics for things like this for clarity - you can safely assume a) yes, you can provide more rigorous statistical assessment of 'how much' besides 'eyeballing it' - although visually obvious things are highly informative, b) the things I mention you can see are indeed (highly) statistically significant etc. etc.]
There are some hints from this forest plot that small study effects could have a role to play. Although very noisy, larger studies (those with narrower horizontal lines lines, because bigger study ~ less uncertainty in effect size) tend to be higher up the plot and have smaller effects. There is a another plot designed to look at this better - a funnel plot.
To orientate: each study is now a point on a scatterplot, with effect size again on the x-axis (right = greater effect). The y-axis is now the standard error: bigger studies have greater precision, and so lower sampling error, so are plotted higher on the y axis. Each point is a single study - all being well, the scatter should look like a (symmetrical) triangle or funnel like those being drawn on the plot.
All is not well here. The scatter is clearly asymmetric and sloping to the right - smaller studies (towards the bottom of the graph) tend towards greater effect sizes. The lines being drawn on the plot make this even clearer. Briefly:
Although a very asymmetric funnel plot is not proof positive of publication bias, findings like this demand careful investigation and cautious interpretation (see generally). It is challenging to assess exactly 'how big a deal is it, though?': statistical adjustiment for biases in the original data is extremely fraught.
But we are comfortably in 'big deal' territory: this finding credibly up-ends HLI's entire analysis:
a) There are different ways of getting a 'pooled estimate' (~~average, or ~~ typical effect size): random effects (where you assume the true effect is rather a distribution of effects from which each study samples from), vs. fixed effects (where there is a single value for the true effect size). Random effects are commonly preferred as - in reality - one expects the true effect to vary, but the results are much more vulnerable to any small study effects/publication bias (see generally). Comparing the random effect vs. the fixed effect estimate can give a quantitative steer on the possible scale of the problem, as well as guide subsequent analysis.[4] Here, the random effect estimate is 0.52, whilst the fixed one is less than half the size: 0.18.
b) There are other statistical methods you could use (more later). One of the easier to understand (but one of the most conservative) goes back to the red dashed line in the funnel plot. You could extrapolate from it to the point where standard error = 0: so the predicted effect of an infinitely large (so infinitely precise) study - and so also where the 'small study effect' is zero. There are a few different variants of these sorts of 'regression methods', but the ones I tried predict effect sizes of such a hypothetical study between 0.17 and 0.05. So, quantitatively, 70-90% cuts of effect size are on the table here.
c) A reason why regression methods methods are conservative as they will attribute as much variation in reported results as possible to differences in study size. Yet there could be alternative explanations for this besides publication bias: maybe smaller studies have different patient populations with (genuinely) greater efficacy, etc.
However, this statistical confounding can go the other way. HLI is not presenting simple meta-analytic results, but rather meta-regressions: where the differences in reported effect sizes are being predicted by differences between and within the studies (e.g. follow-up time, how much therapy was provided, etc.). One of HLI's findings from this work is that psychotherpy with Strongminds-like traits is ~70% more effective than psychotherapy in general (0.8 vs. 0.46). If this is because factors like 'group or individual therapy' correlate with study size, the real story for this could simply be: "Strongminds-like traits are indicators for methodological weaknesses which greatly inflate true effect size, rather than for a more effective therapeutic modality." In HLI's analysis, the latter is presumed, giving about a ~10% uplift to the bottom line results.[5]
1.2) A major issue, and a major mistake to miss
So this is a big issue, and would be revealed by standard approaches. HLI instead used a very non-standard approach (see), novel - as far as I can tell - to existing practice and, unfortunately, inappropriate (cf., point 5): it gives ~ a 10-15% discount (although I'm not sure this has been used in the Strongminds assessment, although it is in the psychotherapy one).
I came across these problems ~6m ago, prompted by a question by Ryan Briggs (someone with considerably greater expertise than my own) asking after the forest and funnel plot. I also started digging into the data in general at the same time, and noted the same key points explained labouriously above: looks like marked heterogeneity and small study effects, they look very big, and call the analysis results into question. Long story short, they said they would take a look at it urgently then report back.
This response is fine, but as my comments then indicated, I did have (and I think reasonably had) HLI on pretty thin ice/'epistemic probation' after finding these things out. You have to make a lot of odd choices to end up this far from normal practice, nonetheless still have to make some surprising oversights too, to end up missing problems which would appear to greatly undermine a positive finding for Strongminds.[6]
1.3) Maintaining this major mistake
HLI fell through this thin ice after its follow-up. Their approach was to try a bunch of statistical techniques to adjust for publication bias (excellent technique), do the same for their cash transfers meta-analysis (sure), then using the relative discounts between them to get an adjustment for psychotherapy vs. cash transfers (good, esp. as adding directly into the multi-level meta-regressions would be difficult). Further, they provided full code and data for replication (great). But the results made no sense whatsoever:
To orientate: each row is a different statistical technique applied to the two meta-analyses (more later). The x-axis is the 'multiple' of Strongminds vs. cash transfers, and the black line is at 9.4x, the previous 'status quo value'. Bars shorter than this means adjusting for publication bias results in an overall discount for Strongminds, and vice-versa.
The cash transfers funnel plot looks like this:
Compared to the psychotherapy one, it basically looks fine: the scatter looks roughly like a funnel, and no massive trend towards smaller studies = bigger effects. So how could so many statistical methods discount the 'obvious small study effect' meta-analysis less than the 'no apparent small study effect' meta-analysis, to give an increased multiple? As I said at the time, the results look like nonsense to the naked eye.
One problem was a coding error in two of the statistical methods (blue and pink bars). The bigger problem is how the comparisons are being done is highly misleading.
Take a step back from all the dividing going on to just look at the effect sizes. The basic, nothing fancy, random effects model applied to the psychotherapy data gives an effect size of 0.5. If you take the average across all the other model variants, you get ~0.3, a 40% drop. For the cash transfers meta-analysis, the basic model gives 0.1, and the average of all the other models is ~0.9, a 10% drop. So in fact you are seeing - as you should - bigger discounts when adjusting the psychotherapy analysis vs. the cash transfers meta-analysis. This is lost by how the divisions are being done, which largely 'play off' multiple adjustments against one another. (see, pt.2). What the graph should look like is this:
Two things are notable: 1) the different models tend to point to a significant drop (~30-40% on average) in effect size; 2) there is a lot of variation in the discount - from ~0 to ~90% (so visual illustration about why this is known to be v. hard to reliably 'adjust'). I think these results oblige something like the following:
Re. write-up: At least including the forest and funnel plots, alongside a description of why they are concerning. Should also include some 'best guess' correction from the above, and noting this has a (very) wide range. Probably warrants 'back to the drawing board' given reliability issues.
Re. overall recommendation: At least a very heavy astericks placed besides the recommendation. Should also highlight both the adjustment and uncertainty in front facing materials (e.g. 'tentative suggestion' vs. 'recommendation'). Probably warrants withdrawal.
Re. general reflection: I think a reasonable evaluator - beyond directional effects - would be concerned about the 'near'(?) miss property of having a major material issue not spotted before pushing a strong recommendation, 'phase 1 complete/mission accomplished' etc. - especially when found by a third party many months after initial publication. They might also be concerned about the direction of travel. When published, the multiplier was 12x; with spillovers, it falls to 9.5%; with spillovers and the typo corrected, it falls to 7.5x; with a 30% best guess correction for publication bias, we're now at 5.3x. Maybe any single adjustment is not recommendation-reversing, but in concert they are, and the track record suggests the next one is more likely to be further down rather than back up.
What happened instead 5 months ago was HLI would read some more and discuss among themselves whether my take on the comparators was the right one (I am, and it is not reasonably controversial, e.g. 1, 2, cf. fn4). Although 'looking at publication bias is part of their intended 'refining' of the Strongminds assessment, there's been nothing concrete done yet.
Maybe I should have chased, but the exchange on this (alongside the other thing) made me lose faith that HLI was capable of reasonably assessing and appropriately responding to criticisms of their work when material to their bottom line.
2) The cost effectiveness guestimate.
[Readers will be relieved ~no tricky stats here]
As I was looking at the meta-analysis, I added my attempt at 'adjusted' effect sizes of the same into the CEA to see what impact they had on the results. To my surprise, not very much. Hence my previous examples about 'Even if the meta-analysis has zero effect the CEA still recommends Strongminds as several times GD', and 'You only get to equipoise with GD if you set all the effect sizes in the CEA to near-zero.'
I noted this alongside my discussion around the meta-analysis 6m ago. Earlier remarks from HLI suggested they accepted these were diagnostic of something going wrong with how the CEA is aggregating information (but fixing it would be done but not as a priority); more recent ones suggest more 'doubling down'.
In any case, they are indeed diagnostic for a lack of face validity. You obviously would, in fact, be highly sceptical if the meta-analysis of psychotherapy in general was zero (or harmful!) that nonetheless a particular psychotherapy intervention was extremely effective. The (pseudo-)bayesian gloss on why is that the distribution of reported effect sizes gives additional information on the likely size of the 'real' effects underlying them. (cf. heterogeneity discussed above) A bunch of weird discrepancies among them, if hard to explain by intervention characteristics, increases the suspicion of weird distortions, rather than true effects, underlie the observations. So increasing discrepancy between indirect and direct evidence should reduce effect size beyond impacts on any weighted average.
It does not help the findings as-is are highly discrepant and generally weird. Among many examples:
I don't know what the magnitude of the directional 'adjustment' would be, as this relies on specific understanding of the likelier explanations for the odd results (I'd guess a 10%+ downward correction assuming I'm wrong about everything else - obviously, much more if indeed 'the vast bulk in effect variation can be explained by sample size +/- registration status of the study). Alone, I think it mainly points to the quantative engine needing an overhaul and the analysis being known-unreliable until it is.
In any case, it seems urgent and important to understand and fix. The numbers are being widely used and relied upon (probably all of them need at least a big public astericks pending developing more reliable technique). It seems particularly unwise to be reassured by "Well sure, this is a downward correction, but the CEA still gives a good bottom line multiple", as the bottom line number may not be reasonable, especially conditioned on different inputs. Even more so to persist in doing so 6m after being made aware of the problem.
These are mentioned in 3a and 3b of my reply to Michael. Point 1 there (kind of related to 3a) would on its own warrant immediate retraction, but that is not a case (yet) of 'maintained' error.
So in terms of 'epistemic probation', I think this was available 6m ago, but closed after flagrant and ongoing 'violations'.
One quote from the Cochrane handbook feels particularly apposite:
Cochrane
This is not the only problem in HLI's meta-regression analysis. Analyses here should be pre-specified (especially if intended as the primary result rather than some secondary exploratory analysis), to limit risks of inadvertently cherry-picking a model which gives a preferred result. Cochrane (see):
HLI does not mention any pre-specification, and there is good circumstantial evidence of a lot of this work being ad hoc re. 'Strongminds-like traits'. HLI's earlier analysis on psychotherapy in general, using most (?all) of the same studies as in their Strongminds CEA (4.2, here), had different variables used in a meta-regression on intervention properties (table 2). It seems likely the change of model happened after study data was extracted (the lack of significant prediction and including a large number of variables for a relatively small number of studies would be further concerns). This modification seems to favour the intervention: I think the earlier model, if applied to Strongminds, gives an effect size of ~0.6.
Briggs comments have a similar theme, suggestive that my attitude does not solely arise from particular cynicism on my part.