Effective Altruism Forum
EA Forum

Hide table of contents
by ArthurF
2 min read 3

6

Cause prioritizationPhilosophyEffective altruism cultureLongtermismMoral philosophyOpinion
Frontpage

This is my first post, and it is only really a question but I have an initial view that I intend to defend further in the context of longtermism. I'm making this post to get initial responses to the distinction in case I have missed something obvious!

When we say that we want to maximise value, do we want to maximise currently instantiated value, or cumulative value up to this point? It seems that this is an important distinction that may have implications on which interventions can be considered to maximise value. I will argue that we should adopt a framework which maximises cumulative value (CV)

The Distinction

Consider a blowout party. I will define this as a truly Hedonistic utility maximising party where everyone overdoses. Everyone experiences a huge amount of welfare for a short time and then nothing. if we care only about Instantaneous Value (IV) at a given time, a value-time graph will look like this: 

 

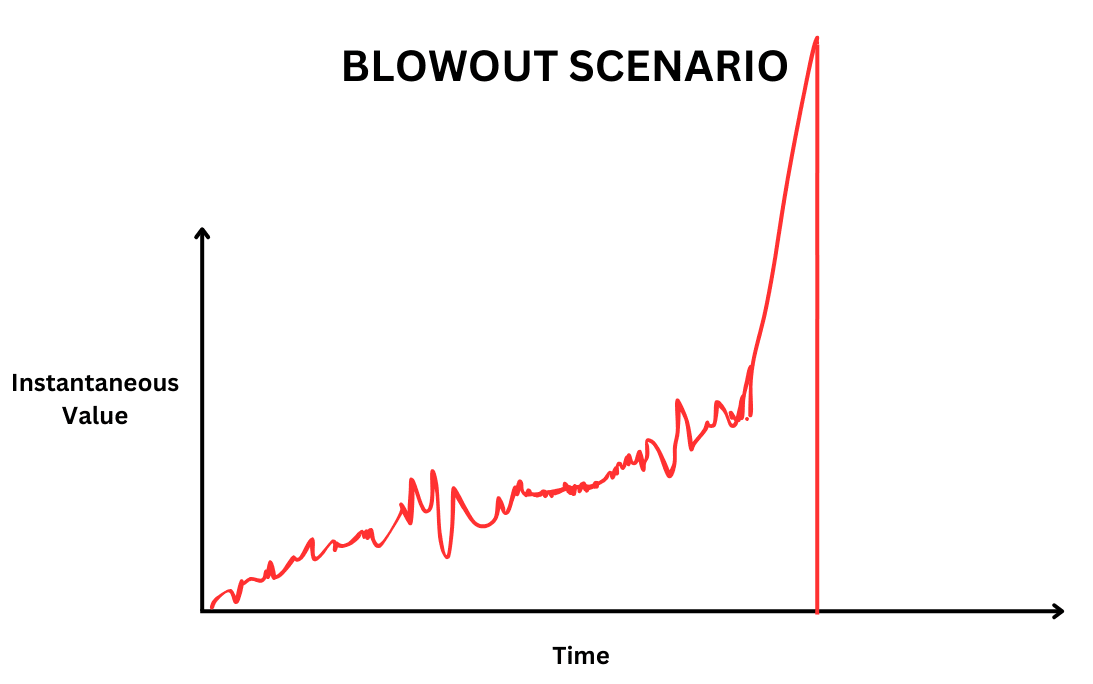
According to the IV framework then, the expected value of the blowout intervention must follow some sort of step function (takes a value and then drops instantly to zero). The intricacies of analysing this calculation are unnecessary, it is only necessary to see that in this case the Blowout scenario will ultimately have neutral expected value.

On the other hand, if we care about maximising Cumulative Value (CV) the graph will instead look like this:

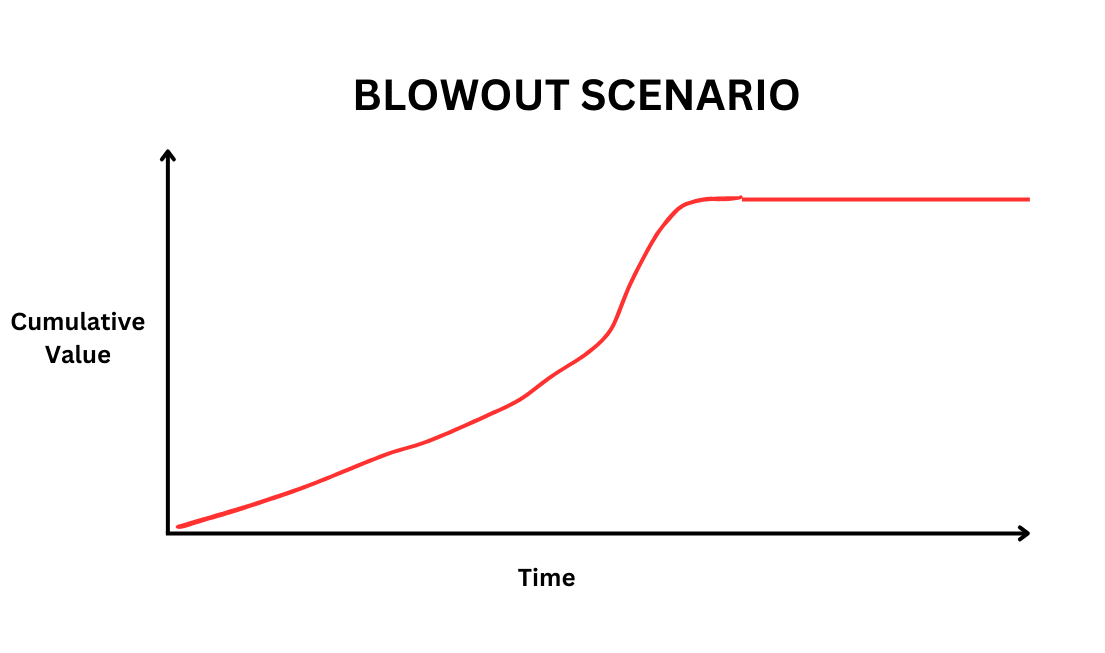
In this framework the expected value of the intervention is proportional to the value introduced. We get all of this additional value added to the overall value of the universe and it remains.

This can be more concisely phrased as whether we care about maximising the y-value of the value-time graph, or whether we care about maximising the integral. In many cases these consequences are correlated but the case described above is a non-unique example in which they diverge. (mathematicians will be able to find trivially many examples of functions where the integral seems not to depend wholly on specific values of y at given points).

Cumulative Value is more intuitive

Intuitively I think this scenario points to caring more about cumulative value. And this makes sense as EAs who are neutral about when and where people exist, it shouldn't matter if a person's high welfare comes now or a person's welfare comes hundreds of years in the future/past. 

Also it seems intuitive that a happy life led now is a good thing. If a person lives a happy life, their death should not remove the value their life added to the world.

How long is an instant

Another question that it is important to ask is how long we may take an instant to be. If we care only about the value being instantiated at any given time, it seems reasonable to ask how long that given period of time is. Practically of course this will make EV calculations incredibly complex. Whereas, if you consider cumulative value, we only need consider the value added by that total project over it's acting period. because the value intoduced is being summed over everything.

Concluding

I am not at all certain of anything said here and would love some conversation about it. In particular I am not certain the noise in the IV graph would not also be present in the CV graph. 

6

0
0

Reactions

0
0

More posts like this

Comments3
Sorted by
New & upvoted
Click to highlight new comments since:
Mich2
1
0

Hi !

Congrats on sharing your first post here !

Sorry for the unpolished bullet points, I’m in a bit if a hurry right now and would probably forget later, but I think it may still be worth it to point out a few things :

  • The way value is defined seems not clearly stated but implicitly guessable to me here. If you look at counterfactual value, the instant value in the blowout scenario could and would probably be negative. It seems to me that you consider value in a non-counterfactual way that attributes zero on the instant scale to nothing existing at all and zero on the cumulative scale to nothing having ever existed. Is that indeed what you have in mind ?
  • About the math : as long as you are integrating a continuous positive function of a real variable on a segment, you’ll get a positive increasing continuously differentiable function. This may help you reflect on the uncertainty you mention at the end regarding noise.
  • I agree with you that CV is more intuitive - I sometimes think theoretically about maximizing or minimizing (just a matter of convention) some integral over spacetime spanning the whole universe for space and its whole period of past, present and future existence for time but that’s impractical. However, I think the way you present your example actually makes things look unintuitive. A party where everyone dies at the end is given a positive value but no, I still wouldn’t attend given the chance. My take is, if you think in terms of counterfactual cumulative value it would be negative, and if you set the zero to nothing having ever existed, your scenario may be positive, but probably less than the scenario that would have happened otherwise.
Reply
ArthurF2
0
0

This makes a lot of sense, Thanks for highlighting the need to define value more explicitly. I'll have a look into this stuff!

on the math point - I don't think that IV would be continuous is the problem, but in general this would mean the noise is present in both frameworks! The case of x^2 sin(1/x) shows the integral of a function with a discontinuity is not necessarily discontinuous but in general discontinuous functions would have a discontinuous integral so the noise doesn't distinguish the frameworks.

Thank you!

Reply
Mich1
0
0

Thanks for your answer !

I thought IV was assumed continuous based on your drawing. Still, I’d be surprised - and I would love to know about it - if you could find an function with a discontinuous integral and does not seem unfit to correctly model IV to me - both out of interest for the mathematical part and of curiosity about what functions we respectively think can correctly model IV.

I think that piecewise continuity and local boundedness are already enough to ensure continuity and almost-everywhere continuous differentiability of the integral. I personally don’t think that functions that don’t match these hypotheses are reasonable candidates for IV, but I would allow IV to take any sign. What are your thoughts on this ?

Reply
More from ArthurF
View more
Curated and popular this week
Relevant opportunities
View more