Introduction
This is a preliminary report on Finite Field Assembly (FF-ASM), a programming language designed to emulate GPUs on regular CPUs using Number Theory and Finite Field Theory.
Finite Field Assembly (FF-ASM) empowers programmers to utilize Number Theory to invent their own math and solve their most immediate tasks.

Use Cases
- Matrix multiplications for Artificial Intelligence.
- Emulate GPU-level parallelization on regular CPUs in specific cases.
- Error-correction coding for Communications.
Finite Field Assembly Language Features
- Finite Field is the primary data structure - FF-asm is a CUDA alternative designed for computations over finite fields.
- Recursive computing support - not cache-aware vectorization, not parallelization, but performing a calculation inside a calculation inside another calculation.
- Recursive computing - performing one outer calculation lets you perform several inner calculations at the same time.
- Extension of C89 - runs everywhere gcc is available.
Low-level systems language - no garbage collector so user handles memory allocation.
Syntax for Finite Field Assembly
Is AI Compute a Hardware or a Software Problem
Sam Altman, the CEO of OpenAI, believes that access to computational resources will become the world's most valuable commodity. His views align with the growing demand for AI and machine learning capabilities among consumers and businesses. A multitude of companies offer hardware-first solutions to satisfy this demand for compute.
The market is saturated with hardware startups focused on delivering compute power for the next generation of AI inference. Custom hardware like Nvidia's GPUs, Groq's TPUs, and Etched's Transformer ASICs aim to address this growing demand for computational resources.
But what if hardware isn't the real bottleneck? Perhaps all our calculations are correct, and the issue lies in the possibility that we're computing in the wrong number system?

Finite Field Assembly: A Language for Inventing Your Own Mathematics
Finite Field Assembly is built on the thesis that mathematics is largely invented rather than discovered. For example, while binary digits (0 and 1) are discovered concepts, binary floating-point arithmetic—the mathematical framework for storing fractions on computers—is entirely invented.
Finite Field Assembly is a programming language designed to empower users to define their own mathematical systems. We provide a framework for creating custom rules, operations, and structures to enable entirely new ways of computation.
The language is built around number theory, congruences and the divisibility properties of primes.
Prime numbers and finite fields serve as fundamental data structures in Finite Field Assembly. This focus permits a unique approach to computation, rooted in mathematical principles rather than conventional programming paradigms.

Getting Started with Finite Field Assembly
Finite Field Assembly (FF-asm), much like CUDA, is an extension of the C programming language. It is built on top of C89, commonly referred to as ANSI C or ISO C, with the goal of ensuring compatibility wherever a standard C compiler is available. This design allows FF-asm to be highly portable and accessible across a wide range of systems.
Installing Dependencies
- One needs a working installation of the GNU MP Bignum library.[1] Here's the link to install libgmp.
- Ubuntu installation instructions here.
- Create a file called
01_HelloWorld.c in the same directory that contains ff_asm_runtime.h and ff_asm_primes.h
Writing Hello World in FF-asm
Remember, FF-asm, just like CUDA, is an extension of C. It's super low-level so you need to hande memory allocations.
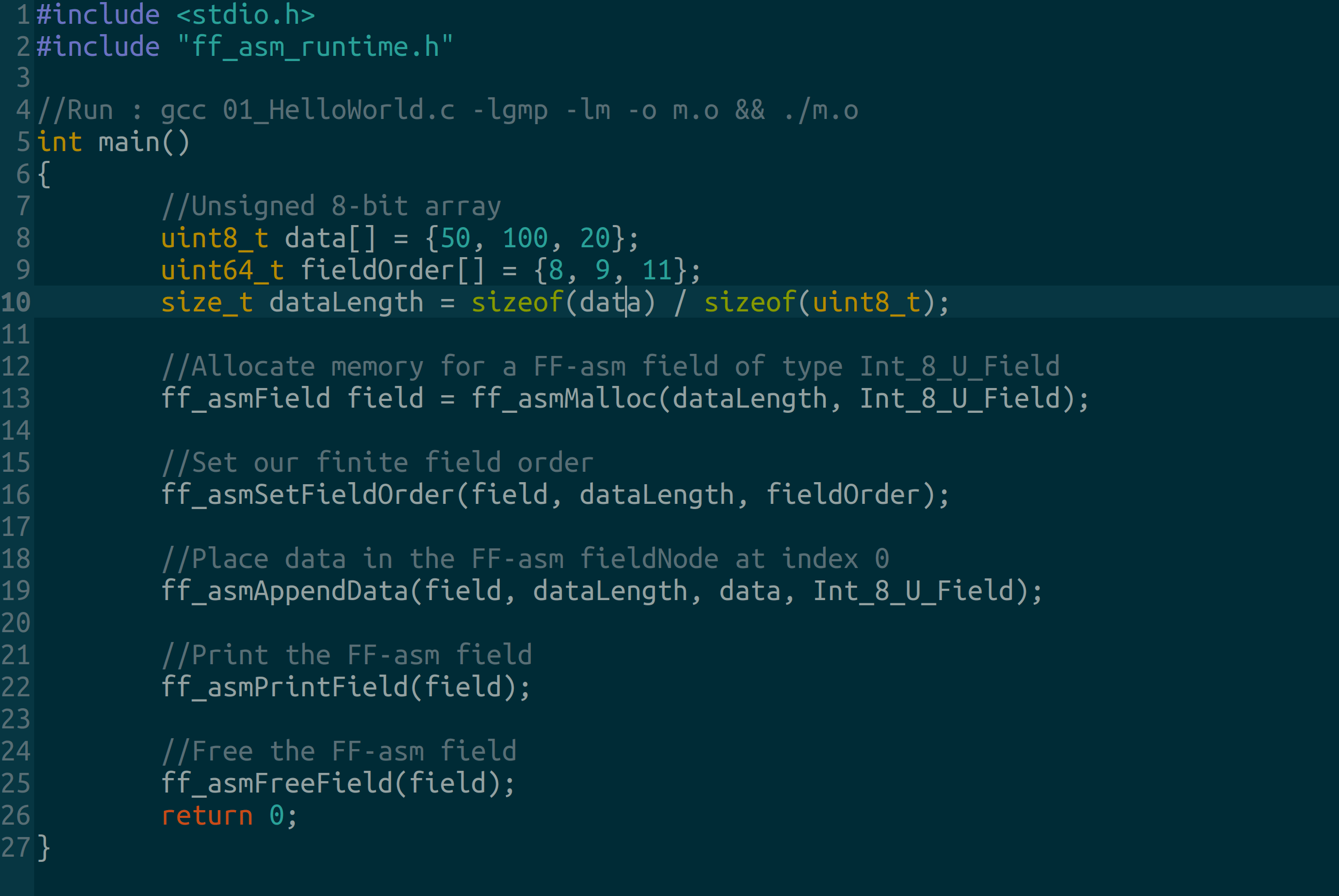
This Hello World Program creates an 8-bit unsigned integer finite field. You can find the source code here.
#include <stdio.h>
#include "ff_asm_runtime.h"
//Run : gcc 01_HelloWorld.c -lgmp -lm -o m.o && ./m.o
int main()
{
//Unsigned 8-bit array
uint8_t data[] = {50, 100, 20};
uint64_t fieldOrder[] = {8, 9, 11};
size_t dataLength = sizeof(data) / sizeof(uint8_t);
//Allocate memory for a FF-asm field of type Int_8_U_Field
ff_asmField field = ff_asmMalloc(dataLength, Int_8_U_Field);
//Set our finite field order
ff_asmSetFieldOrder(field, dataLength, fieldOrder);
//Place data in the FF-asm fieldNode at index 0
ff_asmAppendData(field, dataLength, data, Int_8_U_Field);
//Print the FF-asm field
ff_asmPrintField(field);
//Free the FF-asm field
ff_asmFreeField(field);
return 0;
}Compiling a FF-asm module using GCC
Remember to link libGMP.
$ gcc 01_HelloWorld.c -lgmp -lm -o m.o && ./m.o
$ ./m.oUnderstanding the output of our Print Function
You should observe this output once you compile and run your code.
Field Data Type: Int_8_U_Field
Field Length: 3
Field Node Count: 1
Field Order : 8 9 11
Node Data Type: Int_8_U_Field
Node Data Length: 3
Node Data : 50, 100, 20,
Node integer : 658
Int_8_U_Field: This is the field data type, an unsigned 8-bit integer in this case.(8,9,11): Field order (the number of elements your field can hold). i.e you can store 8 * 9 * 11 elements in the field .658: This is a unique integer that represents your specific the set of finite field elements. It is the solution to a linear congruence.
Next step : Emulating a GPU on a CPU using Number Theory
If you've made this far, we invite you to look further into our documentation here.

You can also
- Support our next research goal - ff-GEMM : Finite Field GEMM Matrix Multiplication
- Star our GitHub repo.